嵌入式软件开发工程师
1.数据结构
数组、链表、栈、队列、树(二叉搜索树)、图
2.算法核心
1.链表
1.1 反转链表
C++/**
* 迭代法实现反转列表
* @param head ListNode类
* @return ListNode类
*/
struct ListNode* ReverseList(struct ListNode* head ) {
// write code here
struct ListNode *Current,*Prev,*next;
Current = head;
Prev = NULL;
while(Current != NULL){
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head = Prev;
return head;
}
1.2 反转指定区间内得链表比如1->2->3->4->5->NULL,m=2,n=3;返回1->4->3->2->5->NULL
C++/**
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
struct ListNode* reverseBetween(struct ListNode* head, int m, int n ) {
// write code here
if(head == NULL)return head;
if(head->next == NULL)return head;
if(m == n)return head;
struct ListNode *Current,*Prev,*next,*start,*start_last;
int i;
Current = head;
Prev = NULL;
next = NULL;
// 先找到开始位置
for (i=1; i<m; i++) {
next = Current->next;
// Current->next = Prev;
Prev = Current;
Current = next;
}
// 标记
start_last = Prev;
start = Current;
// 反转
for (i=0; i<(n-m+1); i++) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
// 头尾节点重指向
if(start != head){
start->next = next;
start_last->next = Prev;//start!=head的情况下，需要保留start上一个指针
}
else {
start->next = next;
head = Prev;//start==head的情况下，直接将head指向待反转的最后一个
}
return head;
}
1.3 输入两个递增的链表，单个链表的长度为n，合并这两个链表并使新链表中的节点仍然是递增排序的。
C++/**
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
struct ListNode* Merge(struct ListNode* pHead1, struct ListNode* pHead2 ) {
// write code here
if(pHead1 == NULL)return pHead2;
if(pHead2 == NULL)return pHead1;
struct ListNode* p1 = (pHead1->val <= pHead2->val ? pHead1 : pHead2);
struct ListNode* p2 = (pHead1->val > pHead2->val ? pHead1 : pHead2);
struct ListNode* p = p1; //p1是主链
// temp存放中间指针，有可能在p1中有可能在p2中，最终每次指向p1链两个node之间和大node最近的那个点
struct ListNode* temp =NULL;
while((p1 != NULL)&&(p2 != NULL)){
if(p1->val <= p2->val){
temp = p1;
p1 = p1->next;
}
else {
temp->next = p2;
temp = p2;
p2 = p2->next;
temp->next = p1;
}
}
if(p1 == NULL){
temp->next =p2;
return p;
}else return p;
}
1.4 合并K个递增的链表，单个链表的长度为n，合并这k链表并使新链表中的节点仍然是递增排序的。 方法一：先将数值存放在一个数组中，排序，再给链表赋新值
C++/**
* @param lists ListNode类一维数组
* @param listsLen int lists数组长度
* @return ListNode类
*/
struct ListNode* mergeKLists(struct ListNode** lists, int listsLen ) {
// write code here
int i=0;
struct ListNode* pHead1 = NULL;
// 找到列表中第一个非空链表
for(i=0;i<listsLen;i++){
if(lists[i] == NULL)continue;
else{
pHead1 = lists[i];//找到后跳出
break;
}
}
// 如果没找到，则列表中全是空的链表，直接返回NULL
if(pHead1 == NULL)return pHead1;
// 接下来进行两个链表的合并
for(i=i+1;i<listsLen;i++){
struct ListNode* pHead2 = lists[i];
if(pHead2 == NULL)continue;
struct ListNode* p1 = (pHead1->val <= pHead2->val ? pHead1 : pHead2);
struct ListNode* p2 = (pHead1->val > pHead2->val ? pHead1 : pHead2);
struct ListNode* p = p1; //p1是主链
// temp存放中间指针，有可能在p1中有可能在p2中，最终每次指向p1链两个node之间和大node最近的那个点
struct ListNode* temp =NULL;
while((p1 != NULL)&&(p2 != NULL)){
if(p1->val <= p2->val){
temp = p1;
p1 = p1->next;
}
else {
temp->next = p2;
temp = p2;
p2 = p2->next;
temp->next = p1;
}
}
// 使用pHead1指向合并的俩链表
if(p1 == NULL){
temp->next =p2;
pHead1 = p;
}else pHead1 = p;
}
return pHead1;
}
方法二、使用自底向上的方法实现归并排序，则可以达到O(nlogn)的时间复杂度、O(1)的空间复杂度。首先求得链表的长度 length，然后将链表拆分成子链表进行合并。
具体做法如下。
- 用 subLength表示每次需要排序的子链表的长度，初始时 subLength=1。
- 每次将链表拆分成若干个长度为 subLength的子链表（最后一个子链表的长度可以小于 subLength，按照每两个子链表一组进行合并，合并后即可得到若干个长度为 subLength×2的有序子链表（最后一个子链表的长度可以小于 subLength×2。合并两个子链表仍然使用「21. 合并两个有序链表」的做法。
- 将 subLength的值加倍，重复第 2 步，对更长的有序子链表进行合并操作，直到有序子链表的长度大于或等于 length，整个链表排序完毕。
C++/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head == nullptr)return head;
int length = 0;
ListNode *node = head;
while(node != nullptr){
length++;
node = node->next;
}
ListNode* dummyHead = new ListNode(0, head);
for(int subLength = 1; subLength < length; subLength <<= 1){
ListNode *pre = dummyHead, *cur = dummyHead->next;
while(cur != nullptr){
ListNode *head1 = cur;
for(int i = 1; i < subLength && cur->next != nullptr; i++){
cur = cur->next;
}
ListNode *head2 = cur->next;
cur->next = nullptr;
cur = head2;
for(int i = 1; i < subLength && cur != nullptr && cur->next != nullptr;i++){
cur = cur->next;
}
ListNode* next = nullptr;
if(cur != nullptr){
next = cur->next;
cur->next = nullptr;
}
ListNode *merged = merge(head1, head2);
pre->next = merged;
while(pre->next != nullptr){
pre = pre->next;
}
cur = next;
}
}
return dummyHead->next;
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
1.5 判断链表中是否有环，思想：使用快慢指针fast和slow，fast 指针每次向后移动两个位置，而slow 指针每次向后移动一个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。
C++/**
* @param head ListNode类
* @return bool布尔型
*/
bool hasCycle(struct ListNode* head ) {
// write code here
//快慢指针
struct ListNode* fast = head;
struct ListNode* slow = head;
while (fast != NULL && slow != NULL) {
if (fast->next != NULL) {
fast = fast->next->next; //快指针每次2步
} else {
return false;
}
slow = slow->next; //慢指针每次1步
if (fast == slow) {
return true;
}
}
return false;
}
1.6 给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。
C++/**
*方法一、使用C语言快慢指针
* @param pHead ListNode类
* @return ListNode类
*/
struct ListNode* EntryNodeOfLoop(struct ListNode* pHead ) {
// write code here
// 方法一、快慢指针
struct ListNode *fast = pHead,*slow = pHead;// 快慢指针一开始都指向头
while(fast){
slow =slow->next; // 慢指针走一步
if(fast->next == NULL)return NULL;// 若快指针的下一步不能走，则说明两指针不会相遇
fast = fast->next->next;// 快指针向后走两步
if(fast == slow){// 找到相交节点, 此时慢指针已经走了nb步
fast = pHead;// 快指针重新移动到头
while(fast != slow){// 直到两指针相遇位置，每次向后走一步
fast = fast->next;
slow = slow->next;
}
return fast;// 找到入口节点，直接返回
}
}
return NULL;
}
/*
*方法二、使用C++语言 哈希表
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
unordered_set<ListNode*> st; // 哈希集合
while(pHead){
if(st.count(pHead)) return pHead; // 若已经记录过，直接返回
st.insert(pHead); // 记录当前结点
pHead = pHead->next;
}
return nullptr; // 无环
}
};
1.7 链表中倒数最后k个结点
C++/**
* @param pHead ListNode类
* @param k int整型
* @return ListNode类
*/
struct ListNode* FindKthToTail(struct ListNode* pHead, int k ) {
// write code here
struct ListNode* Current;
int i = 0, j =0;
Current = pHead;
while (Current != NULL) {
i++;
Current = Current->next;
}
if(i < k)return NULL;
else {
for(j=0;j<(i-k);j++){
pHead = pHead->next;
}
}
return pHead;
}
1.8 输入两个无环的单向链表，找出它们的第一个公共结点，如果没有公共节点则返回空。
C++/*
*方法一：使用C++语言 哈希表
*方法二、使用两个指针分别指向两个链表，其中一个指针走完链表1走链表2，另外一个类似，如果有共同节点，那么最后一起到达末尾，所以第一次相遇的地方就是入口公告节点，如果最后都等于空的话则没有公共节点。
*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
unordered_set<ListNode*> st; // 哈希集合
while(pHead1){
st.insert(pHead1);
pHead1 = pHead1->next;
}
while(pHead2){
if(st.count(pHead2)) return pHead2; // 若已经记录过，直接返回
pHead2 = pHead2->next;
}
return nullptr; // 无环
}
};
1.9 两个链表相加
C++/**
* @param head1 ListNode类
* @param head2 ListNode类
* @return ListNode类
*/
#include <stdlib.h>
struct ListNode* addInList(struct ListNode* head1, struct ListNode* head2 ) {
// write code here
struct ListNode* Current, *Prev, *next;
int i = 0;
//反转链表1
Current = head1;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head1 = Prev;
//反转链表2
Current = head2;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head2 = Prev;
//直接相加
Current = head1;
while (Current) {
Current->val = Current->val + head2->val;
if ((Current->next == NULL) && (head2->next == NULL))break;
else {
if (Current->next == NULL) {
Current->next = head2->next;
break;
}
if (head2->next == NULL) {
break;
}
}
Current = Current->next;
head2 = head2->next;
}
//判断相加后的链表节点值是否大于10，更正
Current = head1;
while(Current){
if(i == 1){
if(Current->val + 1 >= 10){
Current->val = Current->val + 1 - 10;
i = 1;
}
else {
Current->val = Current->val + 1;
i = 0;
}
}
else {
if(Current->val >= 10){
Current->val = Current->val - 10;
i = 1;
}
else {
i = 0;
}
}
Current = Current->next;
}
//再反转
Current = head1;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head1 = Prev;
// 判断第一个值(反转前最后一个值)是否大于10，如果大于则创建一个新的节点
if (i == 1) {
struct ListNode* temp = (struct ListNode*)malloc(sizeof(struct ListNode));
temp->val = 1;
temp->next = head1;
head1 = temp;
}
return head1;
}
1.10 单链表排序
C++/**
* @param head ListNode类 the head node
* @return ListNode类
*/
#include <stdio.h>
struct ListNode* sortInList(struct ListNode* head ) {
// write code here
int NodeVal[100000];
int i = 0;
int len = 0;
int j, temp;
struct ListNode* current = head;
//将链表中的值保存在数组
while (current) {
NodeVal[i] = current->val;
current = current->next;
i++;
}
len = i;
//冒泡排序算法：进行 n-1 轮比较
for (i = 0; i < len - 1; i++) {
//每一轮比较前 n-1-i 个，也就是说，已经排序好的最后 i 个不用比较
for (j = 0; j < len - 1 - i; j++) {
if (NodeVal[j] > NodeVal[j + 1]) {
temp = NodeVal[j];
NodeVal[j] = NodeVal[j + 1];
NodeVal[j + 1] = temp;
}
}
}
//将排序好的数组赋值到链表
i = 0;
current = head;
while (current){
current->val = NodeVal[i++];
current = current->next;
}
return head;
}
1.11 判断一个链表是否为回文结构(即前序 后序遍历一样)
C++/**
* @param head ListNode类 the head
* @return bool布尔型
*/
#include <stdbool.h>
bool isPail(struct ListNode* head ) {
// write code here
struct ListNode *Current,*Prev,*next;
//定义数组存入前序值
int aa[100000];
int i = 0;
Current = head;
while(Current){
aa[i++] = Current->val;
Current = Current->next;
}
// 链表反转
Current = head;
Prev = NULL;
while(Current != NULL){
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head = Prev;
//对比
Current = head;
i = 0;
while(Current){
if(Current->val == aa[i++]){
Current = Current->next;
}
else{
return false;
}
}
return true;
}
1.12 链表的奇偶重排:先奇节点再偶节点如输入1->2->3->4->5->6->null,输出1->3->5->2->4->6->null.
C++/**
* @param head ListNode类
* @return ListNode类
*/
struct ListNode* oddEvenList(struct ListNode* head ) {
// write code here
if(head == NULL)return head;
if(head->next == NULL)return head;
struct ListNode *cur,*forw,*forw1;
cur = head;
forw = forw1 = head->next;
// 奇偶节点跳跳乐
while(cur){
if(cur->next != NULL){
if(cur->next->next != NULL){
cur->next = cur->next->next;
cur = cur->next;
}
else break;
}
else break;
if(forw->next != NULL){
if(forw->next->next != NULL){
forw->next = forw->next->next;
forw = forw->next;
}
}
}
// 当奇数个节点的时候偶数跳跃最后不指向空
if(forw->next != NULL)forw->next = NULL;
// 指向第一个偶节点
cur->next = forw1;
return head;
}
1.13 删除有序链表中重复的元素,删除给出链表中的重复元素（链表中元素从小到大有序），使链表中的所有元素都只出现一次
C++/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param head ListNode类
* @return ListNode类
*/
ListNode* deleteDuplicates(ListNode* head) {
// write code here
if(head == nullptr)return head;
struct ListNode *cur = head,*last = head,*temp;
cur = cur->next;
while (last&&cur) {
if(last->val == cur->val){
// last->next = cur->next;
// last = last->next;
temp = cur;
cur = cur->next;
temp = nullptr;
delete temp;
last->next = cur;
}
else{
cur = cur->next;
last = last->next;
}
}
return head;
}
};
1.14 删除有序链表中重复的元素,给出一个升序排序的链表，删除链表中的所有重复出现的元素，只保留原链表中只出现一次的元素。
C++/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param head ListNode类
* @return ListNode类
*/
ListNode* deleteDuplicates(ListNode* head) {
// write code here
if (head == nullptr)return nullptr;
ListNode* res = new ListNode(0);//在链表前加一个表头
res->next = head;
ListNode* cur = res;
while (cur->next != nullptr && cur->next->next != nullptr) {
//遇到相邻两个节点值相同
if (cur->next->val == cur->next->next->val) {
int temp = cur->next->val;
//将所有相同的都跳过
while (cur->next != nullptr && cur->next->val == temp)
cur->next = cur->next->next;
} else
cur = cur->next;
}
//返回时去掉表头
return res->next;
}
};
2.二分查找/排序
2.1 二分查找
C++class Solution {
public:
/**
* @param nums int整型vector
* @param target int整型
* @return int整型
*/
int search(vector<int>& nums, int target) {
// write code here
int left = 0;
int right = nums.size() - 1;
while(left <= right){
int mid = left + (right - left)/2;
if(nums[mid] == target)return mid;
if(nums[mid] < target){
left = mid + 1;
}
else{
right = mid - 1;
}
}
return -1;
}
};
2.2 寻找峰值
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int findPeakElement(vector<int>& nums) {
// write code here
int left = 0;
int right = nums.size() - 1;
// 二分法
while(left < right){
int mid = (left + right) / 2;
//右边是往下，不一定有坡峰
if(nums[mid] > nums[mid+1]){
right = mid;
}
//右边是往上，一定能找到波峰
else {
left = mid + 1;
}
}
return right;
}
};
2.3 数组中逆序对 在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007 思路：在归并排序过程中，局部有序后，如果一个局部有序的最小值大于另一个局部有序的最大值，那么第一个局部有序后面的值与都可以与第二个局部有序的值构成逆序对，简化了计算时间。
C++class Solution {
private:
const int kmod = 1000000007;
public:
/**
* @param nums int整型vector
* @return int整型
*/
int InversePairs(vector<int>& nums) {
// write code here
int ret = 0;
// 在最外层开辟数组
vector<int> tmp(nums.size());
merge_sort__(nums, tmp, 0, nums.size() - 1, ret);
return ret;
}
void merge_sort__(vector<int>& arr, vector<int>& tmp, int l, int r, int& ret) {
if (l >= r) {
return;
}
int mid = l + ((r - l) >> 1);
merge_sort__(arr, tmp, l, mid, ret);
merge_sort__(arr, tmp, mid + 1, r, ret);
merge__(arr, tmp, l, mid, r, ret);
}
void merge__(vector<int>& arr, vector<int>& tmp, int l, int mid, int r, int& ret) {
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (arr[i] > arr[j]) {
tmp[k++] = arr[j++];
ret += (mid - i + 1);
ret %= kmod;
} else {
tmp[k++] = arr[i++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= r) {
tmp[k++] = arr[j++];
}
for (k = 0, i = l; i <= r; ++i, ++k) {
arr[i] = tmp[k];
}
}
};
2.4 求旋转数组的最小数字,有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。请问，给定这样一个旋转数组，求数组中的最小值。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int minNumberInRotateArray(vector<int>& nums) {
// write code here
int left = 0;
int right = nums.size() - 1;
while(left < right){
int mid = (left + right) / 2;
//最小的数字在mid右边
if(nums[mid] > nums[right]){
left = mid + 1;
}
// 无法判断,一个一个试
else if(nums[mid] == nums[right]) {
right-- ;
}
else {
right = mid;
}
}
return nums[left];
}
};
2.5 你2个版本号version1和version2，请你比较他们的大小。版本号是由修订号组成，修订号与修订号之间由一个"."连接。1个修订号可能有多位数字组成，修订号可能包含前导0，且是合法的。例如，1.02.11，0.1，0.2都是合法的版本号。每个版本号至少包含1个修订号。 修订号从左到右编号，下标从0开始，最左边的修订号下标为0，下一个修订号下标为1，以此类推。
C++#include <iostream>
#include <ostream>
#include <string>
class Solution {
public:
/**
* 比较版本号
* @param version1 string字符串
* @param version2 string字符串
* @return int整型
*/
int compare(string version1, string version2) {
// write code here
int n1 = version1.size();
int n2 = version2.size();
int i = 0, j = 0;
while (i < n1 || j < n2) {
long long num1 = 0;
while (i < n1 && version1[i] != '.') {
num1 = num1 * 10 + version1[i] - '0';
i++;
}
i++;//跳过点
long long num2 = 0;
while (j < n2 && version2[j] != '.') {
num2 = num2 * 10 + version2[j] - '0';
j++;
}
j++;//跳过点
if(num1 > num2)return 1;
if(num1 < num2)return -1;
}
return 0;
}
};
3.二叉树
3.1 二叉树的前序遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Preorder(vector<int> &res, TreeNode* root) {
if (root == nullptr) return;
res.push_back(root->val);
Preorder(res,root->left);
Preorder(res,root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Preorder(result, root);
return result;
}
};
3.2 二叉树的中序遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Inorder(vector<int>&result, TreeNode* root){
if(root == nullptr)return;
Inorder(result, root->left);
result.push_back(root->val);
Inorder(result, root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Inorder(result, root);
return result;
}
};
3.3 二叉树的后续遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Postorder(vector<int> &result, TreeNode* root){
if(root == nullptr)return;
Postorder(result, root->left);
Postorder(result, root->right);
result.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Postorder(result, root);
return result;
}
};
3.4 二叉树的最大深度,此时定义深度是指树的根节点到任一叶子节点路径上节点的数量。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型
*/
int maxDepth(TreeNode* root) {
// write code here
int LeftHeight = 0;
int RightHeight = 0;
if (root == nullptr) {
return 0;
}
LeftHeight = maxDepth(root->left);
RightHeight = maxDepth(root->right);
if (LeftHeight >= RightHeight)return LeftHeight + 1;
else return RightHeight + 1;
}
};
3.5 输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点
C++//方法一 将中序遍历的结果用数组存储下来，得到的数组是有从小到大顺序的。最后将数组中的结点依次连接即可。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<TreeNode*> TreeList;//定义一个数组，根据中序遍历来存储结点。
void inorder(TreeNode* root) {
if (!root) return;
inorder(root->left);
TreeList.push_back(root);
inorder(root->right);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
inorder(pRootOfTree);
for (int i = 0; i < TreeList.size() - 1; i++) { //根据数组中的顺序将结点连接，注意i的范围。
TreeList[i]->right = TreeList[i + 1];
TreeList[i + 1]->left = TreeList[i];
}
return TreeList[0];//数组的头部存储的是双向链表的第一个结点。
}
};
//方法二 根据题目的要求1，不能创建新的结点，而方法一的数组中存储的其实是结点，并不满足题意；所以需要在中序遍历的过程中，直接对结点的指针进行调整。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* preNode;//preNode一定是全局变量。
void inorder(TreeNode* root) {
if (!root) return;
inorder(root->left);
//当前结点中需要进校的调整。
root->left = preNode;
if (preNode) {
preNode->right = root;
}
preNode = root;//更新preNode，指向当前结点，作为下一个结点的前继。
inorder(root->right);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
TreeNode* p = pRootOfTree;
while (p->left) p = p->left;//找到双向链表的开头。
inorder(pRootOfTree);
return p;
}
};
3.6 合并两个二叉树，合并规则是：都存在的结点，就将结点值加起来，否则空的位置就由另一个树的结点来代替。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param t1 TreeNode类
* @param t2 TreeNode类
* @return TreeNode类
*/
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
// write code here
if(t1 == nullptr)return t2;
if(t2 == nullptr)return t1;
TreeNode* head = new TreeNode(t1->val + t2->val);
head->left = mergeTrees(t1->left, t2->left);
head->right = mergeTrees(t1->right, t2->right);
return head;
}
};
3.7 二叉树的镜像，镜像的概念是父节点的左右子节点(及其子孙)交换
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot) {
// write code here
if(pRoot == nullptr)return pRoot;
TreeNode *temp = new TreeNode(0);
temp->left = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = temp->left;
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
}
};
3.8 判断是不是二叉搜索树
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param root TreeNode类
* @return bool布尔型
*/
bool IsSubtreeLesser(struct TreeNode* root, int data) {
if (root == nullptr)return true;
if (root->val <= data
&& IsSubtreeLesser(root->left, data)
&& IsSubtreeLesser(root->right, data))
return true;
else
return false;
}
bool IsSubtreeGreater(struct TreeNode* root, int data) {
if (root == nullptr)return true;
if (root->val >= data
&& IsSubtreeGreater(root->left, data)
&& IsSubtreeGreater(root->right, data))
return true;
else
return false;
}
bool isValidBST(TreeNode* root) {
// write code here
if (root == nullptr)return true;
if (IsSubtreeLesser(root->left, root->val)
&& IsSubtreeGreater(root->right, root->val)
&& isValidBST(root->left)
&& isValidBST(root->right))
return true;
else
return false;
}
};
3.9 判断是不是完全二叉树，若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树。（第 h 层可能包含 [1~2h] 个节点）
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <queue>
class Solution {
public:
/**
* @param root TreeNode类
* @return bool布尔型
*/
bool isCompleteTree(TreeNode* root) {
// write code here
if(root == nullptr)return true;
queue<TreeNode*> q;
q.push(root);
bool flag = false;
//层次遍历
while(!q.empty()){
int sz = q.size();
for(int i = 0; i < sz; i++){
TreeNode* cur = q.front();
q.pop();
//标记第一次遇到空节点
if(cur == nullptr)flag = true;
else {
//后续访问已经遇到空节点了，说明经过了叶子
if(flag)return false;
q.push(cur->left);
q.push(cur->right);
}
}
}
return true;
}
};
3.10 输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树，具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <cstdio>
class Solution {
public:
/**
* @param pRoot TreeNode类
* @return bool布尔型
*/
int maxDepth(TreeNode* root) {
// write code here
int LeftHeight = 0;
int RightHeight = 0;
if (root == nullptr) {
return -1;
}
LeftHeight = maxDepth(root->left);
RightHeight = maxDepth(root->right);
if (LeftHeight >= RightHeight)return LeftHeight + 1;
else return RightHeight + 1;
}
bool IsBalanced_Solution(TreeNode* pRoot) {
// write code here
if(pRoot == nullptr)return true;
int left_h = maxDepth(pRoot->left);
int right_h = maxDepth(pRoot->right);
printf("%d,%d",left_h,right_h);
if((abs(left_h - right_h) <= 1)
&&IsBalanced_Solution(pRoot->left)
&&IsBalanced_Solution(pRoot->right))return true;
else return false;
}
};
3.11 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <cstdio>
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @param p int整型
* @param q int整型
* @return int整型
*/
vector<int> Path(TreeNode* root, int a) {
vector<int> path_v;
TreeNode* temp = root;
while (temp->val != a) {
if (temp->val != a) {
path_v.push_back(temp->val);
}
if (temp->val < a)temp = temp->right;
else temp = temp->left;
}
path_v.push_back(temp->val);
return path_v;
}
int lowestCommonAncestor(TreeNode* root, int p, int q) {
// write code here
// p路径 q路径(包含自身)
vector<int> path_p = Path(root, p);
vector<int> path_q = Path(root, q);
int res;
// 比较两个路径
for (int i = 0; i < min(path_p.size(), path_q.size()); i++) {
if(path_p[i] == path_q[i]){
// 最后一个相同的节点就是最近的公共祖先
res = path_p[i];
}
}
return res;
}
};
3.12 给定一个二叉树，找到指定节点的最近公共祖先（用到了深度搜索，递归方法）
如果返回的是节点值那么路径就定义为vector<int>，如果要返回的是节点就定义为：vector<TreeNode*>；
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @param o1 int整型
* @param o2 int整型
* @return int整型
*/
bool find = false;
void dfs(vector<int>&path, TreeNode* root, int o){
if(find || root == nullptr)return;//已经找到或者到达空节点
path.push_back(root->val);
if(root->val == o){
find = true;
return;
}
dfs(path, root->left, o);
dfs(path, root->right, o);
if(find)return;//防止去除节点
path.pop_back();//不在这条路径上，去除节点
}
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
// write code here
vector<int> path1, path2;
dfs(path1, root, o1);
find = false;
dfs(path2, root, o2);
int res;
for(int i = 0; i < min(path1.size(),path2.size()); i++){
if(path1[i] == path2[i])res = path1[i];
}
return res;
}
};
3.13 序列化和反序列化二叉树，二叉树的序列化(Serialize)是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串。
C++/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
//处理序列化的功能函数（递归）
void SerializeFunction(TreeNode* root, string& str) {
// 如果指针为空，表示左叶子节点或右叶子节点为空，用#表示
if (root == nullptr) {
str += '#';
return;
}
// 根节点
string temp = to_string(root->val);
str += temp + '!';//加！区分节点
// 左右子树
SerializeFunction(root->left, str);
SerializeFunction(root->right, str);
}
char* Serialize(TreeNode* root) {
// 处理空树
if (root == nullptr)return "#";
string res;
SerializeFunction(root, res);
// 把str转换成char
char* charRes = new char[res.length() + 1];
strcpy(charRes, res.c_str());
charRes[res.length()] = '\0';
return charRes;
}
//处理反序列化的功能函数（递归）
TreeNode* DeserializeFunction(char** str) {
//到达叶节点时，构建完毕，返回继续构建父节点
//双**表示取值
if (**str == '#') {
(*str)++;
return nullptr;
}
// 数字转换
int val = 0;
while (**str != '!' && **str != '\0') {
val = val * 10 + ((**str) - '0');
(*str)++;
}
TreeNode* root = new TreeNode(val);
// 序列到底了，构建完成
if (**str = '\0')return root;
else (*str)++;
//反序列化与序列化一致，都是前序
root->left = DeserializeFunction(str);
root->right = DeserializeFunction(str);
return root;
}
TreeNode* Deserialize(char* str) {
if (str == "#")return nullptr;
TreeNode* res = DeserializeFunction(&str);
return res;
}
};
3.14 重建二叉树，给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param preOrder int整型vector
* @param vinOrder int整型vector
* @return TreeNode类
*/
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
int n = preOrder.size();
int m = vinOrder.size();
//每个遍历都不能为0
if (n == 0 || m == 0)
return NULL;
//构建根节点
TreeNode* root = new TreeNode(preOrder[0]);
for (int i = 0; i < vinOrder.size(); i++) {
//找到中序遍历中的前序第一个元素
if (preOrder[0] == vinOrder[i]) {
//左子树的前序遍历
vector<int> leftpre(preOrder.begin() + 1, preOrder.begin() + i + 1);
//左子树的中序遍历
vector<int> leftvin(vinOrder.begin(), vinOrder.begin() + i);
//构建左子树
root->left = reConstructBinaryTree(leftpre, leftvin);
//右子树的前序遍历
vector<int> rightpre(preOrder.begin() + i + 1, preOrder.end());
//右子树的中序遍历
vector<int> rightvin(vinOrder.begin() + i + 1, vinOrder.end());
//构建右子树
root->right = reConstructBinaryTree(rightpre, rightvin);
break;
}
}
return root;
}
};
3.15 请根据二叉树的前序遍历，中序遍历恢复二叉树，并打印出二叉树的右视图
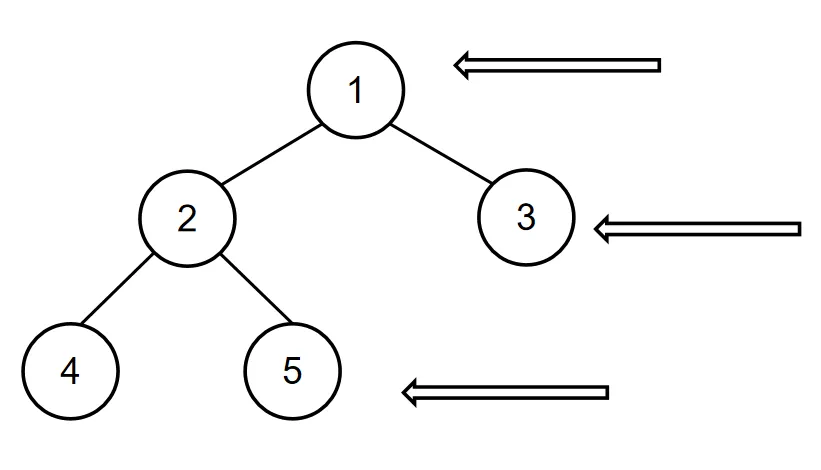
C++#include <stack>
#include <unordered_map>
#include <vector>
class Solution {
public:
/**
* 求二叉树的右视图
* @param preOrder int整型vector 先序遍历
* @param inOrder int整型vector 中序遍历
* @return int整型vector
*/
// 建树
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
int n = preOrder.size();
int m = vinOrder.size();
//每个遍历都不能为0
if (n == 0 || m == 0)
return NULL;
//构建根节点
TreeNode* root = new TreeNode(preOrder[0]);
for (int i = 0; i < vinOrder.size(); i++) {
//找到中序遍历中的前序第一个元素
if (preOrder[0] == vinOrder[i]) {
//左子树的前序遍历
vector<int> leftpre(preOrder.begin() + 1, preOrder.begin() + i + 1);
//左子树的中序遍历
vector<int> leftvin(vinOrder.begin(), vinOrder.begin() + i);
//构建左子树
root->left = reConstructBinaryTree(leftpre, leftvin);
//右子树的前序遍历
vector<int> rightpre(preOrder.begin() + i + 1, preOrder.end());
//右子树的中序遍历
vector<int> rightvin(vinOrder.begin() + i + 1, vinOrder.end());
//构建右子树
root->right = reConstructBinaryTree(rightpre, rightvin);
break;
}
}
return root;
}
// 右视图
vector<int> rightSideView(TreeNode* root){
unordered_map<int, int> map;//存放右边最深处的值
int max_depth = -1;//记录最大深度
stack<TreeNode*> nodes;//维护深度访问节点
stack<int> depths;//维护深度时的深度
nodes.push(root);
depths.push(0);
while(!nodes.empty()){
TreeNode* node = nodes.top();
nodes.pop();
int depth = depths.top();
depths.pop();
if(node != nullptr){
//维护二叉树的最大深度
max_depth = max(max_depth, depth);
//如果不存在对应深度的节点我们才插入，因为后面入栈的时候我后如的右节点的栈
if(map.find(depth) == map.end()){
map[depth] = node->val;
}
nodes.push(node->left);
nodes.push(node->right);
depths.push(depth + 1);
depths.push(depth + 1);
}
}
vector<int> res;
for(int i = 0; i < map.size(); i++){
res.push_back(map[i]);
}
return res;
}
vector<int> solve(vector<int>& preOrder, vector<int>& inOrder) {
// write code here
vector<int> res;
if(preOrder.size() == 0)return res;
// 建树
TreeNode* temp = reConstructBinaryTree(preOrder, inOrder);
return rightSideView(temp);
}
};
4.堆/栈/队列
4.1 使用两个栈模拟一个队列，思路：当插入时，直接插入 stack1，2、当弹出时，当 stack2 不为空，弹出 stack2 栈顶元素，如果 stack2 为空，将 stack1 中的全部数逐个出栈入栈 stack2，再弹出 stack2 栈顶元素
C++class Solution {
public:
void push(int node) {
stack1.push(node);
}
int pop() {
if (stack2.empty()) {
while (!stack1.empty()) {
int temp;
temp = stack1.top();
stack1.pop();
stack2.push(temp);
}
}
int temp2 = stack2.top();
stack2.pop();
return temp2;
}
private:
stack<int> stack1;
stack<int> stack2;
};
4.2 最小栈。定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的 min 函数，输入操作时保证 pop、top 和 min 函数操作时，栈中一定有元素。进阶：栈的各个操作的时间复杂度是O(1) ，空间复杂度是 O(n) 思路：用两个栈来做，另外一个栈保持栈顶元素是最小值。
C++#include <cstddef>
#include <stack>
#include <vector>
class Solution {
public:
void push(int value) {
node.push(value);
//空或者新元素较小，则入栈
if(node_min.empty() || node_min.top() > value)node_min.push(value);
//重复加入栈顶
else node_min.push(node_min.top());
}
void pop() {
node.pop();
node_min.pop();
}
int top() {
return node.top();
}
int min() {
return node_min.top();
}
private:
stack<int> node;
stack<int> node_min;
};
4.3 有效括号序列
C++#include <asm-generic/errno.h>
#include <vector>
class Solution {
public:
/**
* @param s string字符串
* @return bool布尔型
*/
bool isValid(string s) {
// write code here
stack<char> str;
for (int i = 0; i < s.length(); i++) {
if ((s[i] == '(') || (s[i] == '[') || (s[i] == '{') ) {
str.push(s[i]);
}
if ((s[i] == ')') || (s[i] == ']') || (s[i] == '}') ) {
if (s[i] == ')') {
if (!str.empty()) {
if (str.top() == '(') {
str.pop();
continue;
} else return false;
}
else return false;
}
if (s[i] == ']') {
if (!str.empty()) {
if (str.top() == '[') {
str.pop();
continue;
} else return false;
}
else return false;
}
if (s[i] == '}') {
if (!str.empty()) {
if (str.top() == '{') {
str.pop();
continue;
} else return false;
}
else return false;
}
}
}
if (str.empty())return true;
else return false;
}
};
4.4 滑动窗口的最大值，返回滑动窗口大小为size的窗口中的最大值。
C++#include <vector>
class Solution {
public:
/**
* @param num int整型vector
* @param size int整型
* @return int整型vector
*/
vector<int> maxInWindows(vector<int>& num, int size) {
// write code here
vector<int> max_num;
if(size == 0)return max_num;
int max;
for(int i = 0; i < num.size() - size + 1;i++){
max = num[i];
for(int j = i; j < size + i;j++){
if(max < num[j])max = num[j];
}
max_num.push_back(max);
}
return max_num;
}
};
4.5 输出数组最小K个数,思路：优先队列即PriorityQueue，是一种内置的机遇堆排序的容器，分为大顶堆与小顶堆。要找到最小的k个元素，只需要准备k个数字，之后每次遇到一个数字能够快速的与这k个数字中最大的值比较，每次将最大的值替换掉，那么最后剩余的就是k个最小的数字了。
C++class Solution {
public:
/**
* @param input int整型vector
* @param k int整型
* @return int整型vector
*/
vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
// write code here
vector<int> res;
if (k == 0 || input.size() == 0)
return res;
priority_queue<int> q;
//构建一个k个大小的堆
for (int i = 0; i < k; i++)
q.push(input[i]);
for (int i = k; i < input.size(); i++) {
//较小元素入堆
if (q.top() > input[i]) {
q.pop();
q.push(input[i]);
}
}
//堆中元素取出入vector
for (int i = 0; i < k; i++) {
res.push_back(q.top());
q.pop();
}
return res;
}
};
4.6 寻找数组中第K大个数,思路：快速排序(每次移动，可以找到一个标杆元素，然后将大于它的移到左边，小于它的移到右边，由此整个数组划分成为两部分，然后分别对左边和右边使用同样的方法进行排序，不断划分左右子段，直到整个数组有序。这也是分治的思想，将数组分化成为子段，分而治之。)
C++class Solution {
public:
/**
* @param a int整型vector
* @param n int整型
* @param K int整型
* @return int整型
*/
int part(vector<int>& r, int low, int hight) { //划分函数
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j) {
while (i < j &&r[j] <= pivot) { //从右向左开始找一个 大于 pivot的数值
j--;
}
if (i < j) {
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j &&r[i] > pivot) { //从左向右开始找一个 小于 pivot的数值
i++;
}
if (i < j) {
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
int Quicksort(vector<int>& r, int low, int hight, int K) {
int mid;
if (low < hight) {
mid = part(r, low, hight); // 返回基准元素位置
Quicksort(r, low, mid - 1, K); // 左区间递归快速排序
Quicksort(r, mid + 1, hight, K); // 右区间递归快速排序
}
return r[K-1];
}
int findKth(vector<int>& a, int n, int K) {
// write code here
return Quicksort(a, 0, n-1, K);
}
};
4.7 数据流中的中位数。思路：暴力方法，用vector来存取，调用sort函数排序。方法二，插入排序，每次来数据前对原数组进行插入排序。
C++#include <algorithm>
#include <vector>
class Solution {
public:
#define SCD static_cast<double>
vector<int> v;
void Insert(int num) {
if(v.empty())v.push_back(num);
else{
auto it = lower_bound(v.begin(), v.end(), num);
v.insert(it, num);
}
}
double GetMedian() {
int sz = v.size();
if(sz & 1)return SCD(v[sz >> 1]);
else{
return SCD((v[sz >> 1] + v[(sz-1) >> 1])) / 2;
}
}
};
4.8 表达式求值，写一个整数计算器，支持加减乘三种运算和括号。思路：遇到左括号，则将括号后的部分送入递归，处理子问题；
C++#include <cctype>
#include <string>
#include <vector>
class Solution {
public:
/**
* 返回表达式的值
* @param s string字符串 待计算的表达式
* @return int整型
*/
vector<int> function(string s, int index) {
int i;
stack<int> stack;
int num = 0;
char op = '+';
for (i = index; i < s.length(); i++) {
//数字转换成int数字
if (isdigit(s[i])) {
num = num * 10 + s[i] - '0';
if (i != s.length() - 1)continue;
}
//碰到'('时，把整个括号内的当成一个数字处理
if (s[i] == '(') {
//递归处理括号
vector<int> res = function(s, i + 1);
num = res[0];
i = res[1];
if (i != s.length() - 1)continue;
}
switch (op) {
//加减号先入栈
case '+':
stack.push(num);
break;
case '-':
//相反数
stack.push(-num);
break;
//优先计算乘号
case '*':
int temp = stack.top();
stack.pop();
stack.push(temp * num);
break;
}
num = 0;
//右括号结束递归
if (s[i] == ')')
break;
else
op = s[i];
}
int sum = 0;
//栈中元素相加
while (!stack.empty()) {
sum += stack.top();
stack.pop();
}
return vector<int> {sum, i};
}
int solve(string s) {
// write code here
return function(s, 0)[0];
}
};
5.哈希表
5.1 多数元素问题。数组中出现次数超过一半的数字,思路给定一个数组，找出数组中的众数，若有，返回众数，若没有，返回0。有三个方法：哈希表法(先遍历一遍数组，在map中存每个元素出现的次数，然后再遍历一次数组，找出众数)、排序法(使用sort(numbers.begin(),numbers.end())排序，超过一半的数肯定在数组中间)、候选法（最优解）加入数组中存在众数，那么众数一定大于数组的长度的一半。思想就是：如果两个数不相等，就消去这两个数，最坏情况下，每次消去一个众数和一个非众数，那么如果存在众数，最后留下的数肯定是众数。
C++//方法一、哈希表法 /*时间复杂度O(n),空间复杂度O(n)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
unordered_map<int,int> mp;
for(const int val : numbers) ++mp[val];
for(const int val : numbers){
if(mp[val] > (numbers.size() / 2))return val;
}
return 0;
}
};
C++//方法二、排序法，可以先将数组排序，然后可能的众数肯定在数组中间，然后判断一下。 /*时间复杂度O(nlogn),空间复杂度O(n)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
sort(numbers.begin(),numbers.end());
int cond = numbers[numbers.size() / 2];
int cnt;
for(const int k : numbers){
if(cond == k)++cnt;
}
if(cnt > numbers.size() / 2)return cond;
return 0;
}
};
C++//方法三、候选法，/*时间复杂度O(nlogn),空间复杂度O(1)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
int cond = -1;
int cnt = 0;
for(int i = 0; i < numbers.size(); i++){
if(cnt == 0){
cond = numbers[i];
++cnt;
}
else{
if(cond == numbers[i])++cnt;
else --cnt;
}
}
cnt = 0;
for(const int k : numbers){
if(cond == k)++cnt;
}
if(cnt > numbers.size() / 2)return cond;
return 0;
}
};
//方法四、随机化，随机选一个数字计算次数，/时间复杂度O(n),空间复杂度O(1)/
C++class Solution {
public:
int majorityElement(vector<int>& nums) {
while (true) {
int candidate = nums[rand() % nums.size()];
int count = 0;
for (int num : nums)
if (num == candidate)
++count;
if (count > nums.size() / 2)
return candidate;
}
return -1;
}
};
5.2 返回数组中只出现一次的两个数字。一个整型数组里除了两个数字只出现一次，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
C++#include <any>
#include <unordered_map>
#include <vector>
class Solution {
public:
/**
* @param nums int整型vector
* @return int整型vector
*/
vector<int> FindNumsAppearOnce(vector<int>& nums) {
// write code here
unordered_map<int, int> mp;
vector<int> res;
for(const int val : nums){
mp[val]++;
}
for(int i = 0; i < nums.size(); i++){
if(mp[nums[i]] == 1){
res.push_back(nums[i]);
}
}
if(res[0] > res[1])swap(res[0], res[1]);
return res;
}
};
5.3 找到一个数组中缺失的第一个正整数
C++#include <unordered_map>
class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int minNumberDisappeared(vector<int>& nums) {
// write code here
unordered_map<int, int> mp;
int max = 1;
for(const int val : nums){
if(val > 0){
if(val > max)max = val;
mp[val]++;
}
}
for(int i = 1; i < max; i++){
if(mp[i] == 0)return i;
}
return max + 1;
}
};
6.递归/回溯
6.1 没有重复项数字的全排列，给出一组数字，返回该组数字的所有排列，例如：[1,2,3]的所有排列如下[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].思路：递归+回溯
C++#include <utility>
#include <vector>
class Solution {
public:
/**
* @param num int整型vector
* @return int整型vector<vector<>>
*/
void recursion(vector<vector<int>> &res, vector<int> &num, int index){
// 分支进入结尾，找到一种排列
if(index == num.size() - 1)res.push_back(num);
else{
// 遍历后续的元素
for(int i = index; i < num.size(); i++){
// 交换二者
swap(num[i], num[index]);
// 继续往后找
recursion(res, num, index + 1);
// 回溯
swap(num[i], num[index]);
}
}
}
vector<vector<int> > permute(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<vector<int>> res;
recursion(res, num, 0);
return res;
}
};
6.2 有重复项数字的全排列。思路：递归+回溯
C++class Solution {
public:
/**
* @param num int整型vector
* @return int整型vector<vector<>>
*/
void recursion(vector<vector<int>>& res, vector<int>& num, vector<int>& temp,
vector<int>& vis) {
// 分支进入结尾，找到一种排列
if (temp.size() == num.size()) {
res.push_back(temp);
return;
}
for (int i = 0; i < num.size(); i++) {
//如果该元素已经被加入了则不需要再加入了
if (vis[i])continue;
if (i > 0 && num[i - 1] == num[i] && !vis[i - 1])
//当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
continue;
//标记为使用过
vis[i] = 1;
//加入数组
temp.push_back(num[i]);
recursion(res, num, temp, vis);
//回溯
vis[i] = 0;
temp.pop_back();
}
}
vector<vector<int> > permuteUnique(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<int> vis(num.size(), 0);
vector<vector<int>> res;
vector<int> temp;
recursion(res, num, temp, vis);
return res;
}
};
6.3 岛屿的数量，给一个01矩阵，1代表是陆地，0代表海洋， 如果两个1相邻，那么这两个1属于同一个岛。我们只考虑上下左右为相邻。岛屿: 相邻陆地可以组成一个岛屿（相邻:上下左右） 判断岛屿个数。思路：矩阵中多处聚集着1，要想统计1聚集的堆数而不重复统计，那我们可以考虑每次找到一堆相邻的1，就将其全部改成0，而将所有相邻的1改成0的步骤又可以使用深度优先搜索（dfs）：当我们遇到矩阵的某个元素为1时，首先将其置为了0，然后查看与它相邻的上下左右四个方向，如果这四个方向任意相邻元素为1，则进入该元素，进入该元素之后我们发现又回到了刚刚的子问题，又是把这一片相邻区域的1全部置为0，因此可以用递归实现。
C++#include <vector>
class Solution {
public:
/**
* 判断岛屿数量
* @param grid char字符型vector<vector<>>
* @return int整型
*/
void dfs(vector<vector<char>> &grid, int i, int j){
int n = grid.size();
int m = grid[0].size();
// 置为0
grid[i][j] = '0';
// 左右上下四个方向遍历
if(i - 1 >= 0 && grid[i - 1][j] == '1')dfs(grid, i - 1, j);
if(i + 1 < n && grid[i + 1][j] == '1')dfs(grid, i + 1, j);
if(j - 1 >= 0 && grid[i][j - 1] == '1')dfs(grid, i, j - 1);
if(j + 1 < m && grid[i][j + 1] == '1')dfs(grid, i, j + 1);
}
int solve(vector<vector<char> >& grid) {
// write code here
// 空矩阵的情况
int n = grid.size();
if(n == 0)return 0;
int m = grid[0].size();
// 记录岛屿数量
int count = 0;
// 遍历矩阵
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(grid[i][j] == '1'){
count++;
dfs(grid, i, j);
}
}
}
return count;
}
};
6.4 字符串的排列，输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。(可能string中有重复的字符类似有重复数组的全排列)
C++#include <vector>
class Solution {
public:
/**
* @param str string字符串
* @return string字符串vector
*/
void recursion(vector<string>& res, string &num, string& temp,
vector<int>& vis) {
// 分支进入结尾，找到一种排列
if (temp.size() == num.size()) {
res.push_back(temp);
return;
}
for (int i = 0; i < num.size(); i++) {
//如果该元素已经被加入了则不需要再加入了
if (vis[i])continue;
if (i > 0 && num[i - 1] == num[i] && !vis[i - 1])
//当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
continue;
//标记为使用过
vis[i] = 1;
//加入数组
temp.push_back(num[i]);
recursion(res, num, temp, vis);
//回溯
vis[i] = 0;
temp.pop_back();
}
}
vector<string> Permutation(string str) {
// write code here
//先按字典序排序，使重复字符串相邻
sort(str.begin(), str.end());
//标记每个位置的字符是否被使用过s
vector<int> vis(str.size(), 0);
vector<string> res;
string temp;
recursion(res, str, temp, vis);
return res;
}
};
6.5 括号生成，给出n对括号，请编写一个函数来生成所有的由n对括号组成的合法组合。例如，给出n=3，解集为："((()))", "(()())", "(())()", "()()()", "()(())"思路：递归+回溯。
C++#include <string>
#include <vector>
class Solution {
public:
/**
* @param n int整型
* @return string字符串vector
*/
void recursion(int left, int right, string temp, vector<string> &res, int n){
// 左右括号都用完了就加入结果
if(left == n && right == n){
res.push_back(temp);
return;
}
// 使用一次左括号
if(left < n){
recursion(left + 1, right, temp + '(', res, n);
}
// 使用右括号个数必须小于左括号
if(right < n && left > right){
recursion(left, right + 1, temp + ')', res, n);
}
}
vector<string> generateParenthesis(int n) {
// write code here
vector<string> res;
string temp;
recursion(0, 0, temp, res, n);
return res;
}
};
6.6 矩阵最长递增路径
C++#include <vector>
class Solution {
public:
/**
* 递增路径的最大长度
* @param matrix int整型vector<vector<>> 描述矩阵的每个数
* @return int整型
*/
//记录四个方向
int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int n, m;
int dfs(vector<vector<int>>& matrix, vector<vector<int>>& dp, int i, int j) {
if(dp[i][j] != 0)
return dp[i][j];
dp[i][j]++;
for(int k = 0; k < 4; k++){
int nexti = i + dirs[k][0];
int nextj = j + dirs[k][1];
//判断条件
if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] > matrix[i][j])
dp[i][j] = max(dp[i][j], dfs(matrix, dp, nexti, nextj) + 1);
}
return dp[i][j];
}
int solve(vector<vector<int> >& matrix) {
// write code here
int res = 0;
n = matrix.size();
m = matrix[0].size();
if (n == 0 || m == 0)return 0;
//i，j处的单元格拥有的最长递增路径
vector<vector<int>> dp (n, vector <int> (m));
// 遍历矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
res = max(res, dfs(matrix, dp, i, j));
}
}
return res;
}
};
7.动态规划
7.1 斐波那契数列，输入整数n，输出斐波那契数列的第n个值；可以当作动态规划问题；
C++class Solution {
public:
/**
* @param n int整型
* @return int整型
*/
int Fibonacci(int n) {
// write code here
int dp[50]{0};
dp[1] = 1, dp[2] = 1;
for(int i = 3; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
7.2 跳台阶，一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。属于动态规划问题，分三步：1.定义问题；2.分解问题；3.子问题求解； 定义dp[i]是跳上第i个台阶的跳法，因为第i个台阶是i-1跳上去的或者是i-2跳上去的，所以dp[i]=dp[i-1]+dp[i-2]，子问题dp[0] = 1, dp[1] =1;所以可以使用递归方法做了。
C++class Solution {
public:
/**
* @param number int整型
* @return int整型
*/
int jumpFloor(int number) {
// write code here
int dp[50]{0};
dp[0] = 1, dp[1] =1;
for (int i = 2; i <= number; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[number];
}
};
7.3 最小花费爬楼梯，给定一个整数数组cost，其中cost[i] 是从楼梯第i 个台阶向上爬需要支付的费用，下标从0开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
C++#include <vector>
class Solution {
public:
/**
* @param cost int整型vector
* @return int整型
*/
int minCostClimbingStairs(vector<int>& cost) {
// write code here
vector<int> dp(cost.size() + 1, 0);
dp[1] = 0, dp[2] = 0;
for(int i = 2; i <= cost.size(); i++){
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
7.4 两个字符串的最长公共子序列，思路，动态规划，1.定义dp[i][j]表示在s1中以i结尾，s2中以j结尾的字符串的最长公共子序列长度。2.根据“若是i位与j位的字符相等，则该问题可以变成1+dp[i−1][j−1]，若i位与j位的字符不相等，取dp[i][j−1]或者dp[i−1][j]的较大值”补充矩阵dp[i][j]。3.dp的最后一个值就是最大子序列的长度，从最后一个值往前找，找到相等的值然后存起来，往左上角走相等的值对应的行或者列就是相等的字符，保存起来。
C++#include <stack>
#include <string>
#include <vector>
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
*
* longest common subsequence
* @param s1 string字符串 the string
* @param s2 string字符串 the string
* @return string字符串
*/
string LCS(string s1, string s2) {
// write code here
if(s1 == "" || s2 == "")return "-1";
int len1 = s1.length();
int len2 = s2.length();
//dp[i][j]表示s1第i位，s2第j位为止的最长公共子序列长度
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
//遍历两个字符串每个位置求的最长长度
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(s1[i - 1] == s2[j - 1]){
dp[i][j] = 1 + dp[i - 1][j - 1];
}
else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 此时dp[len1][len2]为最大子序列的长度
//从动态规划数组末尾开始找最大子序列
stack<char> s;
int i = len1, j = len2;
while(dp[i][j]){
if(dp[i][j] == dp[i - 1][j])i--;
else if(dp[i][j] == dp[i][j - 1])j--;
else if(dp[i][j] > dp[i-1][j-1]){
i--;
j--;
s.push(s1[i]);
}
}
string res = "";
while(!s.empty()){
res += s.top();
s.pop();
}
return res != "" ? res : "-1"; ;
}
};
7.5 两个字符串的公共子串,思路：设1.dp[i][j]表示在str1中以第i个字符结尾在str2中以第j个字符结尾时的公共子串长度；2.遍历两个字符串填充dp数组，转移方程为：如果遍历到的该位两个字符相等，则此时长度等于两个前一位长度+1，dp[i][j]=dp[i−1][j−1]+1，如果遍历到该位时两个字符不相等，则置为0；每次更新dp[i][j]后，我们维护最大值，并更新该子串结束位置；3最后根据最大值结束位置使用substr即可截取出子串。
C++#include <iterator>
#include <stack>
#include <string>
#include <vector>
class Solution {
public:
/**
* longest common substring
* @param str1 string字符串 the string
* @param str2 string字符串 the string
* @return string字符串
*/
string LCS(string str1, string str2) {
// write code here
int len1 = str1.length();
int len2 = str2.length();
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
int max = 0;
int pos = 0;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1[i - 1] == str2[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = 0;
}
if (dp[i][j] > max){
max = dp[i][j]; // 将最大值放进去
pos = i;
}
}
}
return str1.substr(pos - max, max);
}
};
7.6 不同路径的数目,给定一个m∗n的矩阵，要求从矩阵的左上角走到右下角的不同路径数量(每次只能往下或者往右走). 方法一、递归：step 1：（终止条件） 当矩阵变长n减少到1的时候，很明显只能往下走，没有别的选择了，只有1条路径；同理m减少到1时也是如此。因此此时返回数量为1.step 2：（返回值） 对于每一级都将其两个子问题返回的结果相加返回给上一级。step 3：（本级任务） 每一级都有向下或者向右两种路径选择，分别进入相应分支的子问题。
C++class Solution {
public:
/**
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
// write code here
if(m == 1 || n == 1){
return 1;
}
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
}
};
方法二、动态规划：step 1：用dp[i][j]表示大小为i∗j的矩阵的路径数量，下标从1开始。step 2：（初始条件） 当i或者j为1的时候，代表矩阵只有一行或者一列，因此只有一种路径。step 3：（转移方程） 每个格子的路径数只会来自它左边的格子数和上边的格子数，因此状态转移为dp[i][j]=dp[i−1][j]+dp[i][j−1]。
C++#include <vector>
class Solution {
public:
/**
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
// write code here
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(i == 1){
dp[i][j] = 1;
continue;
}
if(j == 1){
dp[i][j] = 1;
continue;
}
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
};
7.7 给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。 思路：动态规划，1.设dp[i][j]为到矩阵a[i-1][j-1]的最小花费；2.分解：dp[i][j] = min(dp[i-1][j],dp[i][j-1])+a[i-1][j-1]；注意第一行只能从左往右走，第一列只能从上往下走。3.矩阵dp右下角那个元素即为到达该地方的最小花费。
C++class Solution {
public:
/**
* @param matrix int整型vector<vector<>> the matrix
* @return int整型
*/
int minPathSum(vector<vector<int> >& matrix) {
// write code here
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (i == 1) {
dp[i][j] = dp[i][j - 1] + matrix[i - 1][j - 1];;
continue;
}
if (j == 1) {
dp[i][j] = dp[i - 1][j] + matrix[i - 1][j - 1];;
continue;
}
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i - 1][j - 1];
}
}
return dp[m][n];
}
};
7.8 把数字翻译成字符串，有一种将字母编码成数字的方式：'a'->1, 'b->2', ... , 'z->26'。现在给一串数字，返回有多少种可能的译码结果？ 思路：动态规划，step 1：用辅助数组dp表示前i个数的译码方法有多少种。tep 2：对于一个数，我们可以直接译码它，也可以将其与前面的1或者2组合起来译码：如果直接译码，则dp[i]=dp[i−1]；如果组合译码，则dp[i]=dp[i−2]。step 3：对于只有一种译码方式的，选上种dp[i−1]即可，对于满足两种译码方式（10，20不能）则是dp[i−1]+dp[i−2]。step 4：依次相加，最后的dp[length]即为所求答案。
C++class Solution {
public:
/**
* 解码
* @param nums string字符串 数字串
* @return int整型
*/
int solve(string nums) {
// write code here
//排除0
if (nums == "0")
return 0;
//排除只有一种可能的10 和 20
if (nums == "10" || nums == "20")
return 1;
//当0的前面不是1或2时，无法译码，0种
for (int i = 1; i < nums.length(); i++) {
if (nums[i] == '0')
if (nums[i - 1] != '1' && nums[i - 1] != '2')
return 0;
}
//辅助数组初始化为1
vector<int> dp(nums.length() + 1, 1);
for (int i = 2; i <= nums.length(); i++) {
//在11-19，21-26之间的情况
if ((nums[i - 2] == '1' && nums[i - 1] != '0') || (nums[i - 2] == '2' &&
nums[i - 1] > '0' && nums[i - 1] < '7'))
dp[i] = dp[i - 1] + dp[i - 2];
else
dp[i] = dp[i - 1];
}
return dp[nums.length()];
}
};
7.9 兑换零钱,给定数组arr，arr中所有的值都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数。 思路：step 1：可以用dp[i]表示要凑出i元钱需要最小的货币数。step 2：一开始都设置为最大值aim+1，因此货币最小1元，即货币数不会超过aim.step 3：初始化dp[0]=0。step 4：后续遍历1元到aim元，枚举每种面值的货币都可能组成的情况，取每次的最小值即可，转移方程为dp[i]=min(dp[i],dp[i−arr[j]]+1).step 5：最后比较dp[aim]的值是否超过aim，如果超过说明无解，否则返回即可。
C++#include <vector>
class Solution {
public:
/**
* 最少货币数
* @param arr int整型vector the array
* @param aim int整型 the target
* @return int整型
*/
int minMoney(vector<int>& arr, int aim) {
// write code here
if(aim < 1)return 0;
vector<int> dp(aim + 1, aim + 1);
dp[0] = 0;
for(int i = 1; i <= aim; i++){
for(int j = 0; j < arr.size(); j++){
if(arr[j] <= i){
dp[i] = min(dp[i], dp[i - arr[j]] + 1);
}
}
}
return dp[aim] > aim ? -1 : dp[aim];
}
};
7.10 最长上升子序列，给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。 思路：动态规划，step 1：用dp[i]表示到元素i结尾时，最长的子序列的长度，初始化为1，因为只有数组有元素，至少有一个算是递增。step 2：第一层遍历数组每个位置，得到n个长度的子数组。step 3：第二层遍历相应子数组求对应到元素i结尾时的最长递增序列长度，期间维护最大值。step 4：对于每一个到i结尾的子数组，如果遍历过程中遇到元素j小于结尾元素，说明以该元素结尾的子序列加上子数组末尾元素也是严格递增的，因此转移方程为dp[i]=dp[j]+1。
C++class Solution {
public:
/**
* 给定数组的最长严格上升子序列的长度。
* @param arr int整型vector 给定的数组
* @return int整型
*/
int LIS(vector<int>& arr) {
// write code here
if(arr.empty())return 0;
//设置数组长度大小的动态规划辅助数组
vector<int> dp(arr.size(), 1);
int res = 1;
for (int i = 1; i < arr.size(); i++) {
for (int j = 0; j < i; j++) {
//可能j不是所需要的最大的，因此需要dp[i] < dp[j] + 1
if (arr[i] > arr[j] && dp[i] < dp[j] + 1) {
//i点比j点大，理论上dp要加1
dp[i] = dp[j] + 1;
//找到最大长度
res = max(res, dp[i]);
}
}
}
return res;
}
};
7.11 最长回文子串， 思路： 方法一：中心扩散，每个字符都可以尝试作为中心点看，会出现两种情况：可能是类似 aba 的字符串，也可能是类似 abba 的情况；只需要分别计算出以一个和两个字符作为中心点的子串，取出较大的长度即可；从left到right开始向两边扩散、比较，如果相等则继续扩散比较；如果不相等则剪枝，不用再继续扩散比较；计算每次比较的回文子串长度，取最大；时间复杂度 O(N^2)，空间复杂度 O(1)；
C++#include <algorithm>
#include <string>
class Solution {
public:
/**
* @param A string字符串
* @return int整型
*/
int helper(string A, int left, int right) {
while (left >= 0 && right < A.length()) {
if (A[left] == A[right]) {
left--;
right++;
continue;
}
break;
}
// "+1"是因为通过下标计算子串长度
// "-2"是因为上边的while循环是当索引为left和right不想等才退出循环的
// 因此此时的left和right是不满足的，需要舍弃
return right - left + 1 - 2;
}
int getLongestPalindrome(string A) {
// write code here
int n = A.length();
if (n < 2)return n;
int res = 0;
for (int i = 0; i < n; i++) {
int len = max(helper(A, i, i), helper(A, i, i + 1));
res = max(res, len);
}
return res;
}
};
方法二：动态规划,1.维护一个布尔型的二维数组dp，dp[i][j]表示 i 到 j 的子串是否是回文子串; 2.从长度0到字符串长度n进行判断; 3.选定起始下标 i 和终止下标 j， i 和 j 分别为要比较的字符串的左右边界指针; 4.从左右边界字符开始判断，即 A.charAt(i) == A.charAt(j); 5.当相等时，还要判断当前长度 c 是否大于1，不大于则表明只有两个字符的字符串，一个或两个字符肯定是回文串，如“11”; 6.判断的长度大于1时，因为最左右的字符已经相等，因此取决于上一次的子串是否是回文子串, 如 “12121”; 7.更新回文串的最大长度;
C++#include <algorithm>
#include <string>
#include <vector>
class Solution {
public:
/**
* @param A string字符串
* @return int整型
*/
int getLongestPalindrome(string A) {
// write code here
int n = A.length();
vector<vector<bool>> dp(n, vector<bool>(n, false));
int max = 0;
// 字符串长度差 c = j-i，即当前要比较的字符串长度
for(int c = 0; c <= n + 1; c++){
for(int i = 0; i < n -c; i++){
int j = c + i;
if(A[i] == A[j]){
// c <= 1表示只有两个字符的字符串，一个或两个字符肯定是回文串
if(c <= 1)dp[i][j] = true;
else{
// 对于两个字符以上的字符串
// 因为最左右的字符已经相等，因此取决于内层的子串是否是回文子串
dp[i][j] = dp[i + 1 ][j - 1];
}
// 更新回文串的最大长度，c代表判断的子串长度，越来越大
if(dp[i][j])max = c + 1;
}
}
}
return max;
}
};
7.12 数字字符串转换成合法的ip地址。 方法一：枚举法，tep 1：依次枚举这三个点的位置。step 2：然后截取出四段数字。step 3：比较截取出来的数字，不能大于255，且除了0以外不能有前导0，然后才能组装成IP地址加入答案中。
C++#include <string>
#include <vector>
class Solution {
public:
/**
* @param s string字符串
* @return string字符串vector
*/
vector<string> restoreIpAddresses(string s) {
// write code here
vector<string> res;
int n = s.length();
for (int i = 1; i < 4 && i < n - 2; i++) {
for (int j = i + 1; j < i + 4 && j < n - 1; j++) {
for (int k = j + 1; k < j + 4 && k < n; k++) {
if (n - k >= 4) {
continue;
}
string a = s.substr(0, i);
string b = s.substr(i, j - i);
string c = s.substr(j, k - j);
string d = s.substr(k);
//IP每个数字不大于255
if (stoi(a) > 255 || stoi(b) > 255 || stoi(c) > 255 || stoi(d) > 255)
continue;
//排除前导0的情况
if ((a.length() != 1 && a[0] == '0') || (b.length() != 1 && b[0] == '0') ||
(c.length() != 1 && c[0] == '0') || (d.length() != 1 && d[0] == '0'))
continue;
//组装IP地址
string temp = a + "." + b + "." + c + "." + d;
res.push_back(temp);
}
}
}
return res;
}
};
7.13 给定两个字符串 str1 和 str2 ，请你算出将 str1 转为 str2 的最少操作数。 你可以对字符串进行3种操作： 1.插入一个字符 2.删除一个字符 3.修改一个字符。 思路：step 1：初始条件： 假设第二个字符串为空，那很明显第一个字符串子串每增加一个字符，编辑距离就加1，这步操作是删除；同理，假设第一个字符串为空，那第二个字符串每增加一个字符，编剧距离就加1，这步操作是添加。 step 2：状态转移： 状态转移肯定是将dp矩阵填满，那就遍历第一个字符串的每个长度，对应第二个字符串的每个长度。如果遍历到str1[i]和 str2[j]的位置，这两个字符相同，这多出来的字符就不用操作，操作次数与两个子串的前一个相同，因此有dp[i][j]=dp[i−1][j−1]；如果这两个字符不相同，那么这两个字符需要编辑，但是此时的最短的距离不一定是修改这最后一位，也有可能是删除某个字符或者增加某个字符，因此我们选取这三种情况的最小值增加一个编辑距离，即dp[i][j]=min(dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1]))+1。
C++class Solution {
public:
/**
* @param str1 string字符串
* @param str2 string字符串
* @return int整型
*/
int editDistance(string str1, string str2) {
// write code here
int n1 = str1.length();
int n2 = str2.length();
//dp[i][j]表示到str1[i]和str2[j]为止的子串需要的编辑距离
vector<vector<int> > dp(n1 + 1, vector<int>(n2 + 1, 0));
//初始化边界
for (int i = 1; i <= n1; i++)
dp[i][0] = dp[i - 1][0] + 1;
for (int i = 1; i <= n2; i++)
dp[0][i] = dp[0][i - 1] + 1;
//遍历第一个字符串的每个位置
for (int i = 1; i <= n1; i++)
//对应第二个字符串每个位置
for (int j = 1; j <= n2; j++) {
//若是字符相同，此处不用编辑
if (str1[i - 1] == str2[j - 1])
//直接等于二者前一个的距离
dp[i][j] = dp[i - 1][j - 1];
else
//选取最小的距离加上此处编辑距离1
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
return dp[n1][n2];
}
};
7.14 打家劫舍问题1，给定一个整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额(不能连着偷)。 思路，动态规划，step 1：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。 step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。 step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为 dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int rob(vector<int>& nums) {
// write code here
//dp[i]表示长度为i的数组，最多能偷取多少钱
vector<int> dp(nums.size() + 1, 0);
//长度为1只能偷第一家
dp[1] = nums[0];
for (int i = 2; i <= nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
return dp[nums.size()];
}
};
7.15 打家劫舍问题2，数组头尾视为相邻，给定一个长度为n的整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。 思路：动态规划，step 1：使用原先的方案是：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。 step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。 step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。 step 4：此时第一家与最后一家不能同时取到，那么我们可以分成两种情况讨论： 情况1：偷第一家的钱，不偷最后一家的钱。初始状态与状态转移不变，只是遍历的时候数组最后一位不去遍历。 情况2：偷最后一家的请，不偷第一家的钱。初始状态就设定了dp[1]=0，第一家就不要了，然后遍历的时候也会遍历到数组最后一位。 step 5：最后取两种情况的较大值即可。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int rob(vector<int>& nums) {
// write code here
//dp[i]表示长度为i的数组，最多能偷取多少钱
vector<int> dp(nums.size() + 1, 0);
//选择偷了第一家
dp[1] = nums[0];
//最后一家不能偷
for (int i = 2; i < nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
int res = dp[nums.size() - 1];
//清除dp数组，第二次循环
dp.clear();
//不偷第一家
dp[1] = 0;
//可以偷最后一家
for (int i = 2; i <= nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
//选择最大值
return max(res, dp[nums.size()]);
}
};
7.16 打家劫舍问题3，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root。除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。 思路：动态规划，我们可以用 f(o)表示选择 o节点的情况下，o节点的子树上被选择的节点的最大权值和；g(o)表示不选择 o节点的情况下，o节点的子树上被选择的节点的最大权值和；l和 r代表 o的左右孩子。当 o被选中时，o的左右孩子都不能被选中，故 o被选中情况下子树上被选中点的最大权值和为 l 和 r不被选中的最大权值和相加，即 f(o)=g(l)+g(r)。当 o不被选中时，o的左右孩子可以被选中，也可以不被选中。对于 o的某个具体的孩子 x，它对 o的贡献是 x被选中和不被选中情况下权值和的较大值。故 g(o)=max{f(l),g(l)}+max{f(r),g(r)}。至此，我们可以用哈希表来存 f和 g的函数值，用深度优先搜索的办法后序遍历这棵二叉树，我们就可以得到每一个节点的 f和 g。根节点的 f和 g的最大值就是我们要找的答案。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map <TreeNode*, int> f, g;
void dfs(TreeNode* node) {
if (!node) {
return;
}
dfs(node->left);
dfs(node->right);
f[node] = node->val + g[node->left] + g[node->right];
g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
}
int rob(TreeNode* root) {
dfs(root);
return max(f[root], g[root]);
}
};
8.字符串
8.1 字符串变形，对于一个长度为 n 字符串，我们需要对它做一些变形。首先这个字符串中包含着一些空格，就像"Hello World"一样，然后我们要做的是把这个字符串中由空格隔开的单词反序，同时反转每个字符的大小写。 比如"Hello World"变形后就变成了"wORLD hELLO"。 思路：step 1：遍历字符串，遇到小写字母，转换成大写，遇到大写字母，转换成小写，遇到空格正常不变。 step 2：第一次反转整个字符串，这样基本的单词逆序就有了，但是每个单词的字符也是逆的。 step 3：再次遍历字符串，以每个空间为界，将每个单词反转回正常。
C++class Solution {
public:
/**
* @param s string字符串
* @param n int整型
* @return string字符串
*/
string trans(string s, int n) {
// write code here
if (n == 0)
return s;
string res;
for (int i = 0; i < n; i++) {
//大小写转换
if (s[i] <= 'Z' && s[i] >= 'A')
res += s[i] - 'A' + 'a';
else if (s[i] >= 'a' && s[i] <= 'z')
res += s[i] - 'a' + 'A';
else
//空格直接复制
res += s[i];
}
//翻转整个字符串
reverse(res.begin(), res.end());
for (int i = 0; i < n; i++) {
int j = i;
//以空格为界，二次翻转
while (j < n && res[j] != ' ')
j++;
reverse(res.begin() + i, res.begin() + j);
i = j;
}
return res;
}
};
8.2 最长公共前缀，给你一个大小为 n 的字符串数组 strs ，其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀，返回这个公共前缀。 思路：step 1：处理数组为空的特殊情况。 step 2：因为最长公共前缀的长度不会超过任何一个字符串的长度，因此我们逐位就以第一个字符串为标杆，遍历第一个字符串的所有位置，取出字符。 step 3：遍历数组中后续字符串，依次比较其他字符串中相应位置是否为刚刚取出的字符，如果是，循环继续，继续查找，如果不是或者长度不足，说明从第i位开始不同，前面的都是公共前缀。 step 4：如果遍历结束都相同，最长公共前缀最多为第一个字符串。
C++class Solution {
public:
/**
* @param strs string字符串vector
* @return string字符串
*/
string longestCommonPrefix(vector<string>& strs) {
// write code here
int n = strs.size();
//空字符串数组
if (n == 0)
return "";
//遍历第一个字符串的长度
for (int i = 0; i < strs[0].length(); i++) {
char temp = strs[0][i];
//遍历后续的字符串
for (int j = 1; j < n; j++)
//比较每个字符串该位置是否和第一个相同
if (i == strs[j].length() || strs[j][i] != temp)
//不相同则结束
return strs[0].substr(0, i);
}
//后续字符串有整个字一个字符串的前缀
return strs[0];
}
};
8.3 验证IP地址是否有效 思路：step 1：写一个split函数（或者内置函数）。 step 2：遍历IP字符串，遇到.或者:将其分开储存在一个数组中。 step 3：遍历数组，对于IPv4，需要依次验证分组为4，分割不能缺省，没有前缀0或者其他字符，数字在0-255范围内。 step 4：对于IPv6，需要依次验证分组为8，分割不能缺省，每组不能超过4位，不能出现除数字小大写a-f以外的字符。
C++class Solution {
public:
/**
* 验证IP地址
* @param IP string字符串 一个IP地址字符串
* @return string字符串
*/
vector<string> split(string s, string spliter) {
vector<string> res;
int i;
//遍历字符串查找spliter
while ((i = s.find(spliter)) && i != s.npos) {
//将分割的部分加入vector中
res.push_back(s.substr(0, i));
s = s.substr(i + 1);
}
res.push_back(s);
return res;
}
int isIPv4(string IP) {
vector<string> s = split(IP, ".");
if (s.size() != 4)
return false;
for (int i = 0; i < s.size(); i++) {
//不可缺省，有一个分割为零，说明两个点相连
if (s[i].size() == 0)
return false;
//比较数字位数及不为零时不能有前缀零
if (s[i].size() < 0 || s[i].size() > 3 || (s[i][0] == '0' && s[i].size() != 1))
return false;
//遍历每个分割字符串，必须为数字
for (int j = 0; j < s[i].size(); j++)
if (!isdigit(s[i][j]))
return false;
//转化为数字比较，0-255之间
int num = stoi(s[i]);
if (num < 0 || num > 255)
return false;
}
return true;
}
int isIPv6(string IP) {
vector<string> s = split(IP, ":");
//IPv6必定为8组
if (s.size() != 8)
return false;
for (int i = 0; i < s.size(); i++) {
//每个分割不能缺省，不能超过4位
if (s[i].size() == 0 || s[i].size() > 4)
return false;
for (int j = 0; j < s[i].size(); j++) {
//不能出现a-fA-F以外的大小写字符
if (!(isdigit(s[i][j]) || (s[i][j] >= 'a' && s[i][j] <= 'f') ||
(s[i][j] >= 'A' && s[i][j] <= 'F')))
return false;
}
}
return true;
}
string solve(string IP) {
// write code here
if (IP.size() == 0)
return "Neither";
if (isIPv4(IP))
return "IPv4";
else if (isIPv6(IP))
return "IPv6";
return "Neither";
}
};
8.4 大数相加，以字符串的形式读入两个数字，编写一个函数计算它们的和，以字符串形式返回。 数据范围：s.length,t.length≤100000，字符串仅由'0'~‘9’构成 思路：模拟加法运算
C++class Solution {
public:
/**
* 计算两个数之和
* @param s string字符串 表示第一个整数
* @param t string字符串 表示第二个整数
* @return string字符串
*/
string solve(string s, string t) {
// write code here
//若是其中一个为空，返回另一个
if (s.empty())
return t;
if (t.empty())
return s;
//让s为较长的，t为较短的
if (s.length() < t.length())
swap(s, t);
//进位标志
int carry = 0;
//从后往前遍历较长的字符串
for (int i = s.length() - 1; i >= 0; i--) {
//转数字加上进位
int temp = s[i] - '0' + carry;
//转较短的字符串相应的从后往前的下标
int j = i - s.length() + t.length();
//如果较短字符串还有
if (j >= 0)
//转数组相加
temp += t[j] - '0';
//取进位
carry = temp / 10;
//去十位
temp = temp % 10;
//修改结果
s[i] = temp + '0';
}
//最后的进位
if (carry == 1)
s = '1' + s;
return s;
}
};
9.双指针
9.1 判断字符串是否是回文结构(即前序遍历和后序遍历是一样的) 思路：使用双指针，一个指针在队首，一个指针在队尾，比较，首指针往后走，尾指针往前走，判断，一直到队尾指针下标大于队尾指针下标。
C++class Solution {
public:
/**
* @param str string字符串 待判断的字符串
* @return bool布尔型
*/
bool judge(string str) {
// write code here
//首指针
int left = 0;
//尾指针
int right = str.length() - 1;
while(left < right){
if(str[left] != str[right])return false;
left++;
right--;
}
return true;
}
};
9.2 合并区间，给出一组区间，请合并所有重叠的区间。请保证合并后的区间按区间起点升序排列。 输入：[[10,30],[20,60],[80,100],[150,180]] 返回值：[[10,60],[80,100],[150,180]]
C++/**
* struct Interval {
* int start;
* int end;
* Interval(int s, int e) : start(start), end(e) {}
* };
*/
class Solution {
public:
/**
* @param intervals Interval类vector
* @return Interval类vector
*/
static bool cmp(Interval &a, Interval &b) {
return a.start < b.start;
}
vector<Interval> merge(vector<Interval>& intervals) {
// write code here
vector<Interval> res;
if(intervals.size() == 0){
return res;
}
//按照区间首排序
sort(intervals.begin(), intervals.end(), cmp);
//放入第一个区间
res.push_back(intervals[0]);
//遍历后续区间，查看是否与末尾有重叠
for(int i = 1; i < intervals.size(); i++){
//区间有重叠，更新结尾
if(intervals[i].start <= res.back().end)
res.back().end = max(res.back().end, intervals[i].end);
//区间没有重叠，直接加入
else
res.push_back(intervals[i]);
}
return res;
}
};
9.3 反转字符串
C++#include <string>
class Solution {
public:
/**
* 反转字符串
* @param str string字符串
* @return string字符串
*/
string solve(string str) {
// write code here
string res;
int len = str.length();
for(int i = 0; i < len; i++){
res += str[len - 1 - i];
}
return res;
}
};
9.4 最长无重复子数组,给定一个长度为n的数组arr，返回arr的最长无重复元素子数组的长度，无重复指的是所有数字都不相同。子数组是连续的，比如[1,3,5,7,9]的子数组有[1,3]，[3,5,7]等等，但是[1,3,7]不是子数组. 思路：step 1：构建一个哈希表，用于统计数组元素出现的次数。 step 2：窗口左右界都从数组首部开始，每次窗口优先右移右界，并统计进入窗口的元素的出现频率。 step 3：一旦右界元素出现频率大于1，就需要右移左界直到窗口内不再重复，将左边的元素移除窗口的时候同时需要将它在哈希表中的频率减1，保证哈希表中的频率都是窗口内的频率。 step 4：每轮循环，维护窗口长度最大值。
C++#include <map>
#include <unordered_map>
class Solution {
public:
/**
* @param arr int整型vector the array
* @return int整型
*/
int maxLength(vector<int>& arr) {
// write code here
// 哈希表内记录窗口内非重复的数字
unordered_map<int, int> mp;
int res = 0;
// 设置窗口左右界
for(int left = 0,right = 0; right < arr.size(); right++){
mp[arr[right]]++;
while(mp[arr[right]] > 1){
mp[arr[left++]]--;
}
res = max(res, right - left + 1);
}
return res;
}
};
9.5 盛水最多的容器，给定一个数组height，长度为n，每个数代表坐标轴中的一个点的高度，eight[i]是在第i点的高度，请问，从中选2个高度与x轴组成的容器最多能容纳多少水。
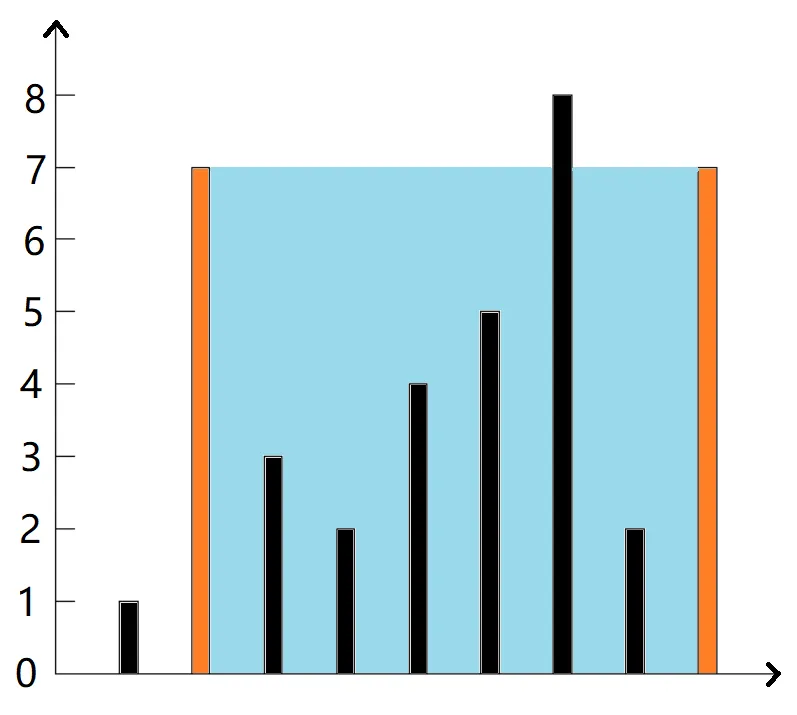思路：可以利用贪心思想：我们都知道容积与最短边长和底边长有关，与长的底边一定以首尾为边，但是首尾不一定够高，中间可能会出现更高但是底边更短的情况，因此我们可以使用对撞双指针向中间靠，这样底边长会缩短，因此还想要有更大容积只能是增加最短变长，此时我们每次指针移动就移动较短的一边，因为贪心思想下较长的一边比较短的一边更可能出现更大容积。
step 1：优先排除不能形成容器的特殊情况。
step 2：初始化双指针指向数组首尾，每次利用上述公式计算当前的容积，维护一个最大容积作为返回值。
step 3：对撞双指针向中间靠，但是依据贪心思想，每次指向较短边的指针向中间靠，另一指针不变。
C++class Solution {
public:
/**
* @param height int整型vector
* @return int整型
*/
int maxArea(vector<int>& height) {
// write code here
//排除不能形成容器的情况
if (height.size() < 2)
return 0;
int res = 0;
//双指针左右界
int left = 0;
int right = height.size() - 1;
//共同遍历完所有的数组
while (left < right) {
//计算区域水容量
int capacity = min(height[left], height[right]) * (right - left);
//维护最大值
res = max(res, capacity);
//优先舍弃较短的边
if (height[left] < height[right])
left++;
else
right--;
}
return res;
}
};
9.6 接雨水问题
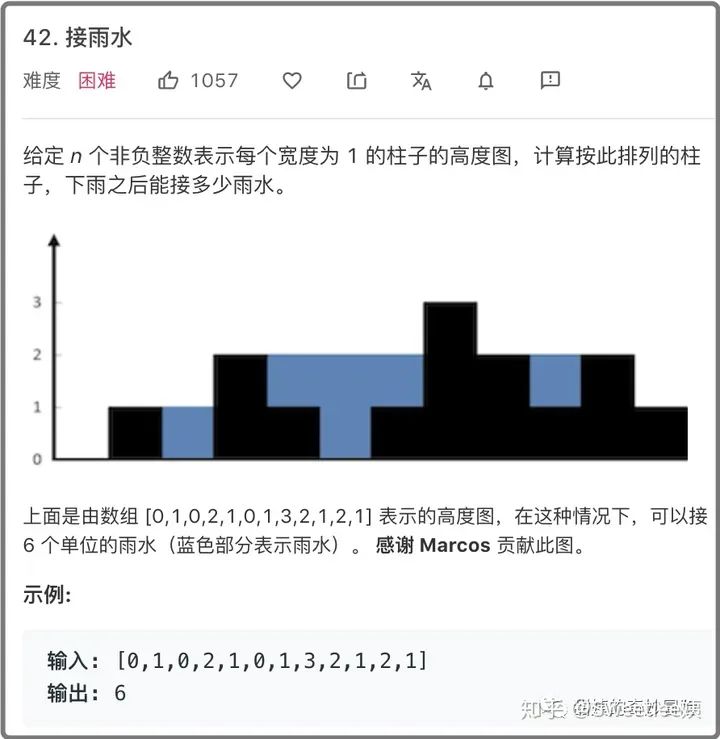
C++// 接雨水问题
#include<iostream>
using namespace std;
/*
*暴力法：每个柱子顶部可以储水的高度为：该柱子的左右两侧最大高度的较小者减去此柱子的高度。因此我们只需要遍历每个柱子，累加每个柱子可以储水的高度即可。
*/
int JieYuShui1(int height[], int len){
int res = 0;
// 遍历每个柱子
for (int i = 1; i < len - 1; i++) {
int leftMax = 0, rightMax = 0;
// 计算当前柱子左侧的柱子中的最大高度
for (int j = 0; j <= i; j++) {
leftMax = max(leftMax, height[j]);
}
// 计算当前柱子右侧的柱子中的最大高度
for (int j = i; j < len; j++) {
rightMax = max(rightMax, height[j]);
}
// 结果中累加当前柱子顶部可以储水的高度，
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
res += min(leftMax, rightMax) - height[i];
}
return res;
}
/*
*动态规划：对于每个柱子，我们都需要从两头重新遍历一遍求出左右两侧的最大高度，这里是有很多重复计算的，很明显最大高度是可以记忆化的，具体在这里可以用数组边递推边存储，也就是常说的动态规划，DP。
1定义二维dp数组 int[][] dp = new int[n][2]，其中，dp[i][0] 表示下标i的柱子左边的最大值，dp[i][1] 表示下标i的柱子右边的最大值。2分别从两头遍历height数组，为 dp[i][0]和 dp[i][1] 赋值。3同方法1，遍历每个柱子，累加每个柱子可以储水的高度。
*/
int JieYuShui2(int height[], int len){
int res = 0;
if (len == 0) {
return 0;
}
// 定义二维dp数组
// dp[i][0] 表示下标i的柱子左边的最大值
// dp[i][1] 表示下标i的柱子右边的最大值
int dp[len][2];
dp[0][0] = height[0];
dp[len - 1][1] = height[len - 1];
for (int i = 1; i < len; i++) {
dp[i][0] = max(height[i], dp[i - 1][0]);
}
for (int i = len - 2; i >= 0; i--) {
dp[i][1] = max(height[i], dp[i + 1][1]);
}
// 遍历每个柱子，累加当前柱子顶部可以储水的高度，
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
for (int i = 1; i < len - 1; i++) {
res += min(dp[i][0], dp[i][1]) - height[i];
}
return res;
}
/*
*双指针：在上述的动态规划方法中，我们用二维数组来存储每个柱子左右两侧的最大高度，但我们递推累加每个柱子的储水高度时其实只用到了 dp[i][0]和 dp[i][1] 两个值，因此我们递推的时候只需要用 int leftMax 和 int rightMax 两个变量就行了。
*/
int JieYuShui3(int height[], int len){
int res = 0;
int leftMax = 0, rightMax = 0, left = 0, right = len - 1;
while (left <= right) {
if (leftMax <= rightMax) {
leftMax = max(leftMax, height[left]);
res += leftMax - height[left++];
} else {
rightMax = max(rightMax, height[right]);
res += rightMax - height[right--];
}
}
return res;
}
int main(){
int arr[] = {0,1,0,2,1,0,1,3,2,1,2,1};
int len = sizeof(arr) / sizeof(arr[0]);
int res = JieYuShui3(arr, len);
cout<<res<<endl;
return 0;
}
10.贪心算法
10.1 主持人调度,有 n 个活动即将举办，每个活动都有开始时间与活动的结束时间，第 i 个活动的开始时间是 starti ,第 i 个活动的结束时间是 endi ,举办某个活动就需要为该活动准备一个活动主持人。 step 1: 利用辅助数组获取单独各个活动开始的时间和结束时间，然后分别开始时间和结束时间进行排序，方便后面判断是否相交。 step 2: 遍历n个活动，如果某个活动开始的时间大于之前活动结束的时候，当前主持人就够了，活动结束时间往后一个。 step 3: 若是出现之前活动结束时间晚于当前活动开始时间的，则需要增加主持人。
C++class Solution {
public:
/**
* 计算成功举办活动需要多少名主持人
* @param n int整型 有n个活动
* @param startEnd int整型vector<vector<>> startEnd[i][0]用于表示第i个活动的开始时间，startEnd[i][1]表示第i个活动的结束时间
* @return int整型
*/
int minmumNumberOfHost(int n, vector<vector<int> >& startEnd) {
vector<int> start;
vector<int> end;
//分别得到活动起始时间
for (int i = 0; i < n; i++) {
start.push_back(startEnd[i][0]);
end.push_back(startEnd[i][1]);
}
//分别对开始和结束时间排序
sort(start.begin(), start.end());
sort(end.begin(), end.end());
int res = 0;
int j = 0;
for (int i = 0; i < n; i++) {
//新开始的节目大于上一轮结束的时间，主持人不变
if (start[i] >= end[j])
j++;
else
//主持人增加
res++;
}
return res;
}
};
11.模拟
11.1 旋转数组，一个数组A中存有 n 个整数，在不允许使用另外数组的前提下，将每个整数循环向右移 M。 输入：6,2,[1,2,3,4,5,6] 返回值：[5,6,1,2,3,4] 思路，先整体反转，再两个局部部分反转。
C++class Solution {
public:
/**
* 旋转数组
* @param n int整型 数组长度
* @param m int整型 右移距离
* @param a int整型vector 给定数组
* @return int整型vector
*/
vector<int> solve(int n, int m, vector<int>& a) {
// write code here
// 取余，因为m可能比n大
m = m % n;
// 第一次全部反转
reverse(a.begin(), a.end());
// 反转开头m个
reverse(a.begin(), a.begin() + m);
// 反转开头n个
reverse(a.begin() + m, a.end());
return a;
}
};
11.2 顺时针旋转矩阵，有一个NxN整数矩阵，请编写一个算法，将矩阵顺时针旋转90度。给定一个NxN的矩阵，和矩阵的阶数N,请返回旋转后的NxN矩阵。 输入[[1,2,3],[4,5,6],[7,8,9]],3 返回[[7,4,1],[8,5,2],[9,6,3]] 思路：先对角线反转(行转列，列转行)，每一行反转
C++class Solution {
public:
/**
* @param mat int整型vector<vector<>>
* @param n int整型
* @return int整型vector<vector<>>
*/
vector<vector<int> > rotateMatrix(vector<vector<int> >& mat, int n) {
// write code here
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
swap(mat[i][j], mat[j][i]);
}
}
for(int i = 0; i < n; i++){
reverse(mat[i].begin(), mat[i].end());
}
return mat;
}
};
11.3 设计LRU缓存结构,设计LRU(最近最少使用)缓存结构，该结构在构造时确定大小，假设大小为 capacity ，操作次数是 n ，并有如下功能:
- Solution(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
- get(key)：如果关键字 key 存在于缓存中，则返回key对应的value值，否则返回 -1 。
- set(key, value)：将记录(key, value)插入该结构，如果关键字 key 已经存在，则变更其数据值 value，如果不存在，则向缓存中插入该组 key-value ，如果key-value的数量超过capacity，弹出最久未使用的key-value
思路：用一个双向链表，哈希表存key以及双向链表的迭代器。当需要插入新的数据项的时候，如果新数据项在链表中存在（一般称为命中），则把该节点移到链表头部，如果不存在，则新建一个节点，放到链表头部，若缓存满了，则把链表最后一个节点删除即可。在访问数据的时候，如果数据项在链表中存在，则把该节点移到链表头部，否则返回-1。这样一来在链表尾部的节点就是最近最久未访问的数据项。
C++#include <unordered_map>
class Solution {
list<pair<int, int>> dlist;//双向链表,pair是key-value的形式
unordered_map<int, list<pair<int, int>>::iterator> map;
int cap;
public:
Solution(int capacity) {
// write code here
cap = capacity;
}
int get(int key) {
// write code here
if (map.count(key)) {
//把这个放在头部，所以需要个tmp存着，然后删掉这个位置，再放到头部
auto tmp = *map[key];
dlist.erase(map[key]);
//map.erase(key);
dlist.push_front(tmp);//把它放在最前面
map[key] = dlist.begin();
//return tmp.second;
return dlist.front().second;
}
return -1;
}
void set(int key, int value) {
// write code here
if (map.count(key)) { //如果存在
dlist.erase(map[key]);//放在头部
//map.erase(key);
} else if (cap == dlist.size()) {
//先删掉末尾的
auto tmp = dlist.back();
map.erase(tmp.first);
dlist.pop_back();
}
dlist.push_front(pair<int, int>(key, value));
map[key] = dlist.begin(); //第一个迭代器
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* solution = new Solution(capacity);
* int output = solution->get(key);
* solution->set(key,value);
*/
11.4 设计LFU缓存结构，set(key, value)：将记录(key, value)插入该结构 get(key)：返回key对应的value值但是缓存结构中最多放K条记录，如果新的第K+1条记录要加入，就需要根据策略删掉一条记录，然后才能把新记录加入。这个策略为：在缓存结构的K条记录中，哪一个key从进入缓存结构的时刻开始，被调用set或者get的次数最少，就删掉这个key的记录；如果调用次数最少的key有多个，上次调用发生最早的key被删除这就是LFU缓存替换算法。实现这个结构，K作为参数给出 思路：但是我们还需要每次最快找到最久未使用的频率最小的节点，这时候我们可以考虑使用一个全局变量，跟踪记录最小的频率，有了最小的频率，怎样直接找到这个频率最小的节点，还是使用哈希表，key值记录各个频率，而value值就是后面接了一串相同频率的节点。如何保证每次都是最小频率的最久为使用，我们用双向链表将统一频率的节点连起来就好了，每次新加入这个频率的都在链表头，而需要去掉的都在链表尾。这样我们方法就是双哈希表。
C++class Solution {
public:
/**
* lfu design
* @param operators int整型vector<vector<>> ops
* @param k int整型 the k
* @return int整型vector
*/
//用list模拟双向链表，双向链表中数组第0位为频率，第1位为key，第2位为val
//频率到双向链表的哈希表
unordered_map<int, list<vector<int> > > freq_mp;
//key到双向链表节点的哈希表
unordered_map<int, list<vector<int> > ::iterator> mp;
//记录当前最小频次
int min_freq = 0;
//记录缓存剩余容量
int size = 0;
vector<int> LFU(vector<vector<int> >& operators, int k) {
// write code here
//记录输出
vector<int> res;
size = k;
//遍历所有操作
for (int i = 0; i < operators.size(); i++) {
auto op = operators[i];
if (op[0] == 1)
//set操作
set(op[1], op[2]);
else
//get操作
res.push_back(get(op[1]));
}
return res;
}
//调用函数时更新频率或者val值
void update(list<vector<int> >::iterator iter, int key, int value) {
//找到频率
int freq = (*iter)[0];
//原频率中删除该节点
freq_mp[freq].erase(iter);
//哈希表中该频率已无节点，直接删除
if (freq_mp[freq].empty()) {
freq_mp.erase(freq);
//若当前频率为最小，最小频率加1
if (min_freq == freq)
min_freq++;
}
//插入频率加一的双向链表表头，链表中对应：freq key value
freq_mp[freq + 1].push_front({freq + 1, key, value});
mp[key] = freq_mp[freq + 1].begin();
}
//set操作函数
void set(int key, int value) {
//在哈希表中找到key值
auto it = mp.find(key);
if (it != mp.end())
//若是哈希表中有，则更新值与频率
update(it->second, key, value);
else {
//哈希表中没有，即链表中没有
if (size == 0) {
//满容量取频率最低且最早的删掉
int oldkey = freq_mp[min_freq].back()[1];
//频率哈希表中删除
freq_mp[min_freq].pop_back();
if (freq_mp[min_freq].empty())
freq_mp.erase(min_freq);
//链表哈希表中删除
mp.erase(oldkey);
}
//若有空闲则直接加入，容量减1
else
size--;
//最小频率置为1
min_freq = 1;
//在频率为1的双向链表表头插入该键
freq_mp[1].push_front({1, key, value});
//哈希表key值指向链表中该位置
mp[key] = freq_mp[1].begin();
}
}
//get操作函数
int get(int key) {
int res = -1;
//查找哈希表
auto it = mp.find(key);
if (it != mp.end()) {
auto iter = it->second;
//根据哈希表直接获取值
res = (*iter)[2];
//更新频率
update(iter, key, res);
}
return res;
}
};
4.力扣top100
1.1每日温度，下一个更大元素。给一个数组，找到下一个比自身大的值在后面第几个。
输入：[73,74,75,71,69,72,76,73] 输出：[1,1,4,2,1,1,0,0] 思路一：暴力法，两层for循环。
C++class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int flag = 0;
vector<int> res;
int cnt = 0;
int len = temperatures.size();
for(int i = 0; i < len; i++){
for(int j = i + 1; j < len; j++){
if(temperatures[j] <= temperatures[i]){
cnt++;
}
if(temperatures[j] > temperatures[i]){
cnt++;
flag = 1;
break;
}
}
if(flag ==1 && cnt < len - i){
res.push_back(cnt);
}
else{
res.push_back(0);
}
cnt = 0;
flag = 0;
}
return res;
}
};
思路二：单调栈,空间换时间，定义一个栈存放数组元素的下标，遍历数组依次将数组元素的下标入栈，分三种情况考虑：
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
C++class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> st;
vector<int> result(temperatures.size(), 0);
st.push(0);
for (int i = 1; i < temperatures.size(); i++) {
// 情况一
if (temperatures[i] < temperatures[st.top()]) {
st.push(i);
}
// 情况二
else if (temperatures[i] == temperatures[st.top()]) {
st.push(i);
}
// 情况三
else {
while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
}
return result;
}
};
1.2 最大的正方形，在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。
思路：动态规划，用dp(i,j)表示以(i,j)为右下角，且只包含1的正方形的边长最大值。 如果该位置的值是0，则 dp(i,j)=0，因为当前位置不可能在由1组成的正方形中； 如果该位置的值是 1，则 dp(i,j)的值由其上方、左方和左上方的三个相邻位置的 dp值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 1，状态转移方程如下： dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1 此外，还需要考虑边界条件。如果 i和 j中至少有一个为 0，则以位置 (i,j)为右下角的最大正方形的边长只能是1，因此 dp(i,j)=1。
C++class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};
1.3实现Trie(前缀树)，前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。
请你实现 Trie 类：
- Trie() 初始化前缀树对象。
- void insert(String word) 向前缀树中插入字符串 word 。
- boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。
C++class Trie {
private:
bool isEnd;
Trie* next[26];
public:
Trie() {
isEnd = false;
memset(next, 0, sizeof(next));
}
void insert(string word) {
Trie* node = this;
for (char c : word) {
if (node->next[c-'a'] == NULL) {
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this;
for (char c : word) {
node = node->next[c - 'a'];
if (node == NULL) {
return false;
}
}
return node->isEnd;
}
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->next[c-'a'];
if (node == NULL) {
return false;
}
}
return true;
}
};
1.4课程优先学习问题，你这个学期必须选修 numCourses 门课程。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi]，表示如果要学习课程 ai 则必须先学习课程 bi。请你判断是否可能完成所有课程的学习？
思路：本题是一道经典的「拓扑排序」问题。我们将每一门课看成一个节点；如果想要学习课程 AAA 之前必须完成课程 BBB，那么我们从 B到 A连接一条有向边。这样以来，在拓扑排序中，B一定出现在 A的前面。我们可以将深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点。我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候，我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。
C++class Solution {
private:
vector<vector<int>> edges;
vector<int> visited;
bool valid = true;
public:
void dfs(int u) {
visited[u] = 1;
for (int v: edges[u]) {
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
else if (visited[v] == 1) {
valid = false;
return;
}
}
visited[u] = 2;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
visited.resize(numCourses);
for (const auto& info: prerequisites) {
edges[info[1]].push_back(info[0]);
}
for (int i = 0; i < numCourses && valid; ++i) {
if (!visited[i]) {
dfs(i);
}
}
return valid;
}
};
1.5除自身以外数组的乘积，可以使用数组元素所有相乘再除以每个值得到，只需要考虑一下0的问题即可。如果要求不使用除法，则用下面的方法做。
思路：我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。对于给定索引 i，我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。
- 初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
- 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]。
- 同理，对于数组 R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1]。
- 当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]。
C++class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
// L 和 R 分别表示左右两侧的乘积列表
vector<int> L(length, 0), R(length, 0);
vector<int> answer(length);
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
};
1.6最大乘积子数组，给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
思路：动态规划，如果我们用f(i) 来表示以第 i个元素结尾的乘积最大子数组的乘积，a表示输入参数 nums，那么很容易推导出这样的状态转移方程：f(i)=max{f(i−1)×ai,ai}，但是这里需要考虑负数的问题，考虑当前位置如果是一个负数的话，那么我们希望以它前一个位置结尾的某个段的积也是个负数，这样就可以负负得正，并且我们希望这个积尽可能「负得更多」，可以得到这样的动态规划转移方程： fmax(i)=max{fmax(i−1)×ai,fmin(i−1)×ai,ai} fmin(i)=min{fmax(i−1)×ai,fmin(i−1)×ai,ai}
C++class Solution {
public:
int maxProduct(vector<int>& nums) {
vector <int> maxF(nums), minF(nums);
for (int i = 1; i < nums.size(); ++i) {
maxF[i] = max(maxF[i - 1] * nums[i], max(nums[i], minF[i - 1] * nums[i]));
minF[i] = min(minF[i - 1] * nums[i], min(nums[i], maxF[i - 1] * nums[i]));
}
return *max_element(maxF.begin(), maxF.end());
}
};
1.7单词拆分，给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
思路：动态规划，我们定义 dp[i]表示字符串 s前 i个字符组成的字符串 s[0..i−1]是否能被空格拆分成若干个字典中出现的单词。我们需要枚举 s[0..i−1]中的分割点 j ，看 s[0..j−1]组成的字符串 s1和 s[j..i−1]组成的字符串 s2拼接成的字符串也同样合法。出如下转移方程：dp[i]=dp[j] && check(s[j..i−1])对于检查一个字符串是否出现在给定的字符串列表里一般可以考虑哈希表来快速判断。
C++class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
auto wordDictSet = unordered_set <string> ();
for (auto word: wordDict) {
wordDictSet.insert(word);
}
auto dp = vector <bool> (s.size() + 1);
dp[0] = true;
for (int i = 1; i <= s.size(); ++i) {
for (int j = 0; j < i; ++j) {
if (dp[j] && wordDictSet.find(s.substr(j, i - j)) != wordDictSet.end()) {
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
};
1.8最长连续序列的长度
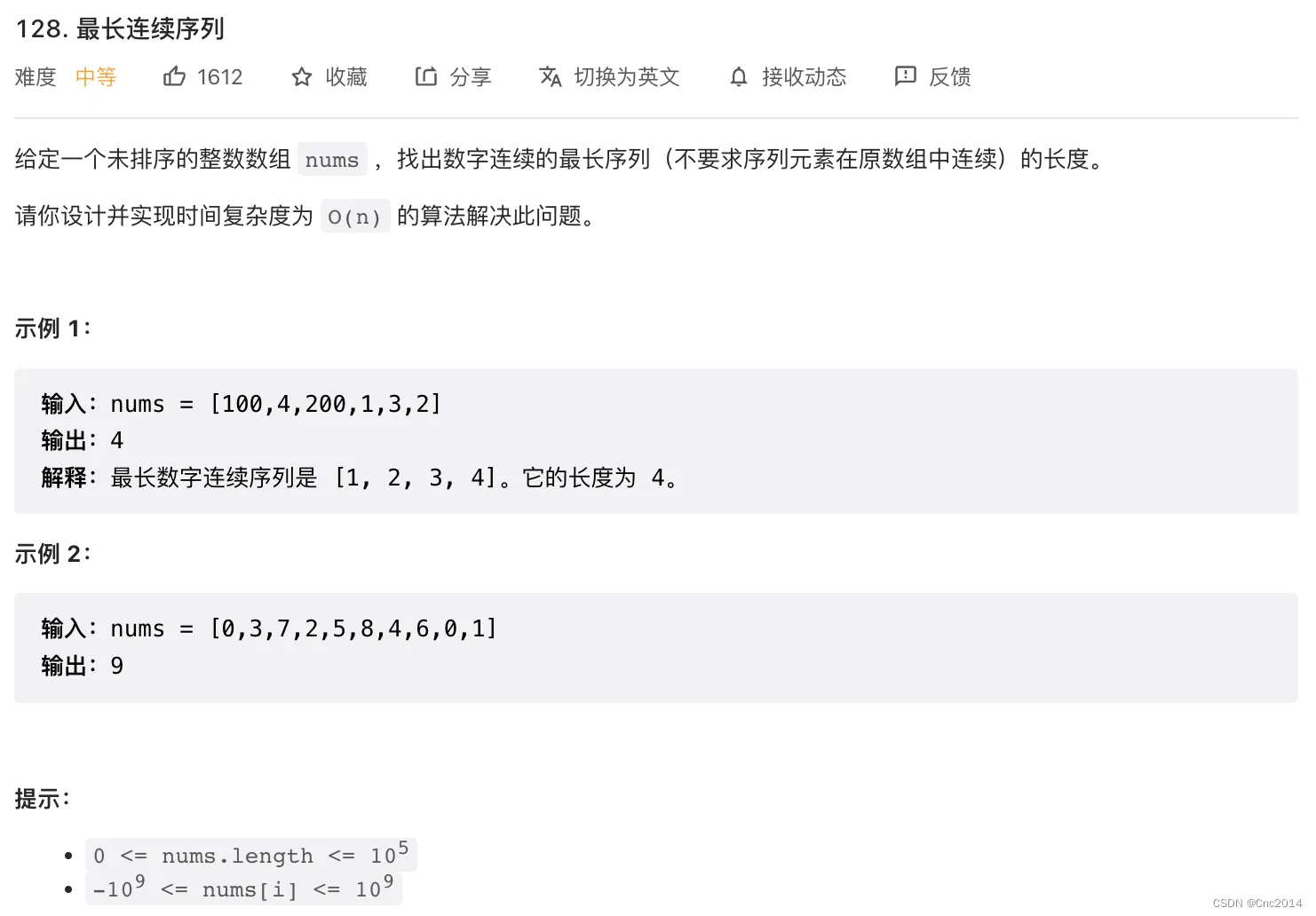思路：哈希表，考虑枚举数组中的每个数 xxx，考虑以其为起点，不断尝试匹配 x+1,x+2,⋯是否存在，假设最长匹配到了 x+y，那么以 x为起点的最长连续序列即为 x,x+1,x+2,⋯ ,x+y其长度为 y+1，我们不断枚举并更新答案即可。仔细分析这个过程，我们会发现其中执行了很多不必要的枚举，如果已知有一个 x,x+1,x+2,⋯ ,x+y的连续序列，而我们却重新从 x+1，x+2或者是 x+y处开始尝试匹配，那么得到的结果肯定不会优于枚举 x为起点的答案，因此我们在外层循环的时候碰到这种情况跳过即可。
那么怎么判断是否跳过呢？由于我们要枚举的数 x一定是在数组中不存在前驱数 x−1的，不然按照上面的分析我们会从 x−1开始尝试匹配，因此我们每次在哈希表中检查是否存在 x−1即能判断是否需要跳过了。
C++class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> num_set;
for (const int& num : nums) {
num_set.insert(num);
}
int longestStreak = 0;
for (const int& num : num_set) {
if (!num_set.count(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.count(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = max(longestStreak, currentStreak);
}
}
return longestStreak;
}
};
1.9二叉树的最大路径和，二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。路径和 是路径中各节点值的总和。
输入：root = [1,2,3] 输出：6 解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6 思路：递归，实现一个简化的函数 maxGain(node)，该函数计算二叉树中的一个节点的最大贡献值，具体而言，就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径，使得该路径上的节点值之和最大。根据函数 maxGain 得到每个节点的最大贡献值之后，如何得到二叉树的最大路径和？对于二叉树中的一个节点，该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，如果子节点的最大贡献值为正，则计入该节点的最大路径和，否则不计入该节点的最大路径和。维护一个全局变量 maxSum 存储最大路径和，在递归过程中更新 maxSum 的值，最后得到的 maxSum 的值即为二叉树中的最大路径和。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int maxSum = INT_MIN;
public:
int maxGain(TreeNode* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时，才会选取对应子节点
int leftGain = max(maxGain(node->left), 0);
int rightGain = max(maxGain(node->right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node->val + leftGain + rightGain;
// 更新答案
maxSum = max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node->val + max(leftGain, rightGain);
}
int maxPathSum(TreeNode* root) {
maxGain(root);
return maxSum;
}
};
1.10目标和，给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
思路： 方法一、回溯，数组 nums的每个元素都可以添加符号 +或 -，因此每个元素有 2 种添加符号的方法，n个数共有 2^n种添加符号的方法，对应2^n种不同的表达式。当 n个元素都添加符号之后，即得到一种表达式，如果表达式的结果等于目标数 target，则该表达式即为符合要求的表达式。
C++class Solution {
public:
int count = 0;
int findTargetSumWays(vector<int>& nums, int target) {
backtrack(nums, target, 0, 0);
return count;
}
void backtrack(vector<int>& nums, int target, int index, int sum) {
if (index == nums.size()) {
if (sum == target) {
count++;
}
} else {
backtrack(nums, target, index + 1, sum + nums[index]);
backtrack(nums, target, index + 1, sum - nums[index]);
}
}
};
方法二、动态规划，记数组的元素和为 sum，添加 -号的元素之和为 neg，则其余添加 +的元素之和为 sum−neg，得到的表达式的结果为(sum−neg)−neg=sum−2⋅neg=target即neg=(sum−target)/2;若上式成立，问题转化成在数组 nums中选取若干元素，使得这些元素之和等于 neg，计算选取元素的方案数。我们可以使用动态规划的方法求解。
C++class Solution {
public:
int count = 0;
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int& num : nums) {
sum += num;
}
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int n = nums.size(), neg = diff / 2;
vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int num = nums[i - 1];
for (int j = 0; j <= neg; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= num) {
dp[i][j] += dp[i - 1][j - num];
}
}
}
return dp[n][neg];
}
};
1.11汉明距离，两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
方法一、使用内置函数，大多数编程语言都内置了计算二进制表达中 111 的数量的函数。在工程中，我们应该直接使用内置函数。
C++class Solution {
public:
int hammingDistance(int x, int y) {
return __builtin_popcount(x ^ y);
}
};
方法二、移位实现位计数，具体地，记 s=x⊕y，我们可以不断地检查 s的最低位，如果最低位为1，那么令计数器加一，然后我们令 s整体右移一位，这样 s的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0为止。这样计数器中就累计了 s的二进制表示中 1的数量。
C++class Solution {
public:
int hammingDistance(int x, int y) {
int s = x ^ y, ret = 0;
while (s) {
ret += s & 1;
s >>= 1;
}
return ret;
}
};
1.12找到数组中所有消失的数字，
思路：我们可以用一个哈希表记录数组 nums中的数字，由于数字范围均在 [1,n]中，记录数字后我们再利用哈希表检查 [1,n]中的每一个数是否出现，从而找到缺失的数字。由于数字范围均在 [1,n]中，我们也可以用一个长度为 n的数组来代替哈希表。这一做法的空间复杂度是 O(n)的。我们的目标是优化空间复杂度到 O(1)。由于 nums的数字范围均在 [1,n]中，我们可以利用这一范围之外的数字，来表达「是否存在」的含义。具体来说，遍历 nums，每遇到一个数 x，就让 nums[x−1]增加 n。由于 nums中所有数均在 [1,n]中，增加以后，这些数必然大于 n。最后我们遍历 nums，若 nums[i]未大于 n，就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。
C++class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n = nums.size();
for (auto& num : nums) {
int x = (num - 1) % n;
nums[x] += n;
}
vector<int> ret;
for (int i = 0; i < n; i++) {
if (nums[i] <= n) {
ret.push_back(i + 1);
}
}
return ret;
}
};
1.13找到字符串中所有字母异位词，给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。 思路：滑动窗口法，根据题目要求，我们需要在字符串 s 寻找字符串 p 的异位词。因为字符串 p 的异位词的长度一定与字符串 p 的长度相同，所以我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口，并在滑动中维护窗口中每种字母的数量；当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时，则说明当前窗口为字符串 p 的异位词。
C++class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int sLen = s.size(), pLen = p.size();
if (sLen < pLen) {
return vector<int>();
}
vector<int> ans;
vector<int> sCount(26);
vector<int> pCount(26);
for (int i = 0; i < pLen; ++i) {
sCount[s[i] - 'a']++;
pCount[p[i] - 'a']++;
}
if (sCount == pCount) {
ans.push_back(0);
}
for (int i = 0; i < sLen - pLen; ++i) {
sCount[s[i] - 'a']--;
sCount[s[i + pLen] - 'a']++;
if (sCount == pCount) {
ans.push_back(i + 1);
}
}
return ans;
}
};
1.14 路径总和2，给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
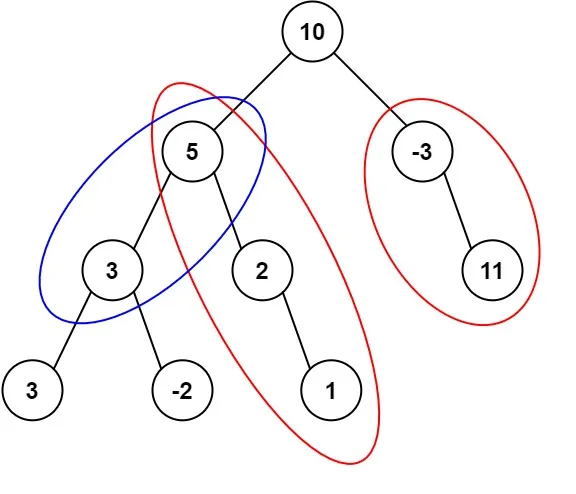
思路：深度优先搜索，我们首先想到的解法是穷举所有的可能，我们访问每一个节点 node，检测以 node为起始节点且向下延深的路径有多少种。我们递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rootSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = 0;
if (root->val == targetSum) {
ret++;
}
ret += rootSum(root->left, targetSum - root->val);
ret += rootSum(root->right, targetSum - root->val);
return ret;
}
int pathSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root->left, targetSum);
ret += pathSum(root->right, targetSum);
return ret;
}
};
1.15分割等和子集，给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
思路：动态规划，给定一个只包含正整数的非空数组 nums[0]，判断是否可以从数组中选出一些数字，使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0−1背包问题」。这道题与传统的「0−1背包问题」的区别在于，传统的「0−1背包问题」要求选取的物品的重量之和不能超过背包的总容量，这道题则要求选取的数字的和恰好等于整个数组的元素和的一半。类似于传统的「0−1 背包问题」，可以使用动态规划求解。 创建二维数组 dp，包含 nnn 行 target+1列，其中 dp[i][j]表示从数组的 [0,i][0,i][0,i] 下标范围内选取若干个正整数（可以是 0个），是否存在一种选取方案使得被选取的正整数的和等于j。初始时，dp中的全部元素都是 false。
C++class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return false;
}
int sum = accumulate(nums.begin(), nums.end(), 0);
int maxNum = *max_element(nums.begin(), nums.end());
if (sum & 1) {
return false;
}
int target = sum / 2;
if (maxNum > target) {
return false;
}
vector<vector<int>> dp(n, vector<int>(target + 1, 0));
for (int i = 0; i < n; i++) {
dp[i][0] = true;
}
dp[0][nums[0]] = true;
for (int i = 1; i < n; i++) {
int num = nums[i];
for (int j = 1; j <= target; j++) {
if (j >= num) {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n - 1][target];
}
};
1.16根据身高重建队列，假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。
思路：从低到高考虑
C++class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](const vector<int>& u, const vector<int>& v) {
return u[0] < v[0] || (u[0] == v[0] && u[1] > v[1]);
});
int n = people.size();
vector<vector<int>> ans(n);
for (const vector<int>& person: people) {
int spaces = person[1] + 1;
for (int i = 0; i < n; ++i) {
if (ans[i].empty()) {
--spaces;
if (!spaces) {
ans[i] = person;
break;
}
}
}
}
return ans;
}
};
1.17除法求值，给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。
思路：广度优先搜索，我们可以将整个问题建模成一张图：给定图中的一些点（变量），以及某些边的权值（两个变量的比值），试对任意两点（两个变量）求出其路径长（两个变量的比值）。 因此，我们首先需要遍历 equations数组，找出其中所有不同的字符串，并通过哈希表将每个不同的字符串映射成整数。 在构建完图之后，对于任何一个查询，就可以从起点出发，通过广度优先搜索的方式，不断更新起点与当前点之间的路径长度，直到搜索到终点为止。
C++class Solution {
public:
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
int nvars = 0;
unordered_map<string, int> variables;
int n = equations.size();
for (int i = 0; i < n; i++) {
if (variables.find(equations[i][0]) == variables.end()) {
variables[equations[i][0]] = nvars++;
}
if (variables.find(equations[i][1]) == variables.end()) {
variables[equations[i][1]] = nvars++;
}
}
// 对于每个点，存储其直接连接到的所有点及对应的权值
vector<vector<pair<int, double>>> edges(nvars);
for (int i = 0; i < n; i++) {
int va = variables[equations[i][0]], vb = variables[equations[i][1]];
edges[va].push_back(make_pair(vb, values[i]));
edges[vb].push_back(make_pair(va, 1.0 / values[i]));
}
vector<double> ret;
for (const auto& q: queries) {
double result = -1.0;
if (variables.find(q[0]) != variables.end() && variables.find(q[1]) != variables.end()) {
int ia = variables[q[0]], ib = variables[q[1]];
if (ia == ib) {
result = 1.0;
} else {
queue<int> points;
points.push(ia);
vector<double> ratios(nvars, -1.0);
ratios[ia] = 1.0;
while (!points.empty() && ratios[ib] < 0) {
int x = points.front();
points.pop();
for (const auto [y, val]: edges[x]) {
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;
points.push(y);
}
}
}
result = ratios[ib];
}
}
ret.push_back(result);
}
return ret;
}
};
1.18字符串解码，给定一个经过编码的字符串，返回它解码后的字符串。编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。
输入：s = "3[a]2[bc]" 输出："aaabcbc"
输入：s = "3[a2[c]]" 输出："accaccacc"
思路：栈操作，本题中可能出现括号嵌套的情况，比如 2[a2[bc]]，这种情况下我们可以先转化成 2[abcbc]，在转化成 abcbcabcbc。我们可以把字母、数字和括号看成是独立的 TOKEN，并用栈来维护这些 TOKEN。具体的做法是，遍历这个栈： 如果当前的字符为数位，解析出一个数字（连续的多个数位）并进栈 如果当前的字符为字母或者左括号，直接进栈 如果当前的字符为右括号，开始出栈，一直到左括号出栈，出栈序列反转后拼接成一个字符串，此时取出栈顶的数字（此时栈顶一定是数字，想想为什么？），就是这个字符串应该出现的次数，我们根据这个次数和字符串构造出新的字符串并进栈 重复如上操作，最终将栈中的元素按照从栈底到栈顶的顺序拼接起来，就得到了答案。注意：这里可以用不定长数组来模拟栈操作，方便从栈底向栈顶遍历。
C++class Solution {
public:
string getDigits(string &s, size_t &ptr) {
string ret = "";
while (isdigit(s[ptr])) {
ret.push_back(s[ptr++]);
}
return ret;
}
string getString(vector <string> &v) {
string ret;
for (const auto &s: v) {
ret += s;
}
return ret;
}
string decodeString(string s) {
vector <string> stk;
size_t ptr = 0;
while (ptr < s.size()) {
char cur = s[ptr];
if (isdigit(cur)) {
// 获取一个数字并进栈
string digits = getDigits(s, ptr);
stk.push_back(digits);
} else if (isalpha(cur) || cur == '[') {
// 获取一个字母并进栈
stk.push_back(string(1, s[ptr++]));
} else {
++ptr;
vector <string> sub;
while (stk.back() != "[") {
sub.push_back(stk.back());
stk.pop_back();
}
reverse(sub.begin(), sub.end());
// 左括号出栈
stk.pop_back();
// 此时栈顶为当前 sub 对应的字符串应该出现的次数
int repTime = stoi(stk.back());
stk.pop_back();
string t, o = getString(sub);
// 构造字符串
while (repTime--) t += o;
// 将构造好的字符串入栈
stk.push_back(t);
}
}
return getString(stk);
}
};
1.19 前 K 个高频元素，给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
思路：粗暴排序法但是时间复杂度高，基于快速排序可以实现(内部找到)
C++class Solution {
public:
void qsort(vector<pair<int, int>>& v, int start, int end, vector<int>& ret, int k) {
int picked = rand() % (end - start + 1) + start;
swap(v[picked], v[start]);
int pivot = v[start].second;
int index = start;
for (int i = start + 1; i <= end; i++) {
// 使用双指针把不小于基准值的元素放到左边，
// 小于基准值的元素放到右边
if (v[i].second >= pivot) {
swap(v[index + 1], v[i]);
index++;
}
}
swap(v[start], v[index]);
if (k <= index - start) {
// 前 k 大的值在左侧的子数组里
qsort(v, start, index - 1, ret, k);
} else {
// 前 k 大的值等于左侧的子数组全部元素
// 加上右侧子数组中前 k - (index - start + 1) 大的值
for (int i = start; i <= index; i++) {
ret.push_back(v[i].first);
}
if (k > index - start + 1) {
qsort(v, index + 1, end, ret, k - (index - start + 1));
}
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
// 获取每个数字出现次数
unordered_map<int, int> occurrences;
for (auto& v: nums) {
occurrences[v]++;
}
vector<pair<int, int>> values;
for (auto& kv: occurrences) {
values.push_back(kv);
}
vector<int> ret;
qsort(values, 0, values.size() - 1, ret, k);
return ret;
}
};
1.20 买卖股票的最佳时机，给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0。
思路：一次遍历，一直记录最小值，然后当前值和最小值作差。
C++class Solution {
public:
int maxProfit(vector<int>& prices) {
int inf = 1e9;
int minprice = inf, maxprofit = 0;
for(int i = 0; i < prices.size(); i++){
maxprofit = max(maxprofit, prices[i] - minprice);
minprice = min(prices[i], minprice);
}
return maxprofit;
}
};
1.21，戳气球，有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。求所能获得硬币的最大数量。
思路：为了方便处理，我们对 nums数组稍作处理，将其两边各加上题目中假设存在的 nums[−1]和 nums[n]，并保存在 val数组中，即 val[i]=nums[i−1]。之所以这样处理是为了处理 nums[−1]，防止下标越界。我们观察戳气球的操作，发现这会导致两个气球从不相邻变成相邻，使得后续操作难以处理。于是我们倒过来看这些操作，将全过程看作是每次添加一个气球。我们定义方法 solve，令 solve(i,j)表示将开区间 (i,j)内的位置全部填满气球能够得到的最多硬币数。由于是开区间，因此区间两端的气球的编号就是 i和 j，对应着 val[i]和 val[j]。
C++class Solution {
public:
vector<vector<int>> rec;
vector<int> val;
int solve(int left, int right) {
if (left >= right - 1) {
return 0;
}
if (rec[left][right] != -1) {
return rec[left][right];
}
for (int i = left + 1; i < right; i++) {
int sum = val[left] * val[i] * val[right];
sum += solve(left, i) + solve(i, right);
rec[left][right] = max(rec[left][right], sum);
}
return rec[left][right];
}
int maxCoins(vector<int>& nums) {
int n = nums.size();
val.resize(n + 2);
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
val[0] = val[n + 1] = 1;
rec.resize(n + 2, vector<int>(n + 2, -1));
return solve(0, n + 1);
}
};
1.22买卖股票的最佳时机，含冷冻期，用户可以多次买卖股票，卖出股票后一天不能卖出(冷冻期)。
思路：动态规划，
class Solution { public: int maxProfit(vector<int>& prices) { if (prices.empty()) { return 0; } int n = prices.size(); // f[i][0]: 手上持有股票的最大收益 // f[i][1]: 手上不持有股票，并且处于冷冻期中的累计最大收益 // f[i][2]: 手上不持有股票，并且不在冷冻期中的累计最大收益 vector<vector<int>> f(n, vector<int>(3)); f[0][0] = -prices[0]; for (int i = 1; i < n; ++i) { f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]); f[i][1] = f[i - 1][0] + prices[i]; f[i][2] = max(f[i - 1][1], f[i - 1][2]); } return max(f[n - 1][1], f[n - 1][2]); } };
1.23删除无效括号,给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。返回所有可能的结果。答案可以按 任意顺序 返回。
思路：
C++class Solution {
public:
vector<string> res;
vector<string> removeInvalidParentheses(string s) {
int lremove = 0;
int rremove = 0;
for(char c : s){
if(c == '('){
lremove++;
}
else if(c == ')'){
if(lremove == 0)rremove++;
else lremove--;
}
}
helper(s, 0, lremove, rremove);
return res;
}
void helper(string str, int start, int lremove, int rremove){
if(lremove == 0 && rremove == 0){
if(isValid(str))res.push_back(str);
return;
}
for(int i = start; i < str.size(); i++){
if(i != start && str[i] == str[i - 1])continue;
// 如果剩余的字符无法满足去掉的数量要求，直接返回
if (lremove + rremove > str.size() - i) {
return;
}
// 尝试去掉一个左括号
if (lremove > 0 && str[i] == '(') {
helper(str.substr(0, i) + str.substr(i + 1), i, lremove - 1, rremove);
}
// 尝试去掉一个右括号
if (rremove > 0 && str[i] == ')') {
helper(str.substr(0, i) + str.substr(i + 1), i, lremove, rremove - 1);
}
}
}
inline bool isValid(const string & str){
int cnt = 0;
for(int i = 0; i < str.size(); i++){
if(str[i] == '(')cnt++;
else if(str[i] == ')'){
cnt--;
if(cnt < 0)return false;
}
}
return cnt == 0;
}
};
1.24 思路：
5.笔试经历
1.1 美团实习笔试第一题，小美入职美团后。特别喜欢meituan里的 mt这2个字符。他想写一份代码找到字符串里所有的'mf，"MT"。"mT"或者“Mt”。然后把他们都变成$$。请你写一份代码帮助也实现。
C++#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
getline(cin, s);
for (size_t i = 0; i < s.length() - 1; ++i) {
if (s[i] == 'm' || s[i] == 'M') {
if (s[i + 1] == 't' || s[i + 1] == 'T') {
s.replace(i, 2, "$$");
i++;
}
}
}
cout << s << endl;
return 0;
}
1.2 美团实习笔试第二题，小美拿到了一个n×n 的矩阵，其中每个元素是 0 或者 1。小美认为一个矩形区域是完美的，当且仅当该区域内 0 的数量恰好等于 1 的数量。现在，小美希望你回答有多少个i×i的完美矩形区域。
输入
4 1010 0101 1100 0011
输出
0 7 0 1
C++#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000;
int n;
char str[N][N];
int m[N][N], s[N][N];
int ans[N];
int GetPreSub(int x1, int y1, int x2, int y2) {
return s[x2 + 1][y2 + 1] - s[x1][y2 + 1] - s[x2 + 1][y1] + s[x1][y1];
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> str[i];
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
if (str[i][j] == '1') {
m[i + 1][j + 1] = 1;
} else {
m[i + 1][j + 1] = 0;
}
}
}
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + m[i][j];
}
}
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
for (int k = 0; k < n; k ++) {
if(i + k >= n || j + k >= n) {
break;
}
int sub = GetPreSub(i, j, i + k, j + k);
if (sub * 2 == (k + 1) * (k + 1)) {
ans[k] ++;
}
}
}
}
for (int i = 0; i < n; i ++) cout << ans[i] << endl;
return 0;
}
1.3 美团机器人招聘题1：第一行输入一个正整数n，代表菜品总数。第二行输入n个正整数ai,代表每道菜的价格。第三行输入两个正整数x和y,x代表满减的价格，y代表红包的价格。计算订单总价。
C++/*第一行输入一个正整数n，代表菜品总数。第二行输入n个正整数ai,代表每道菜的价格。
第三行输入两个正整数x和y,x代表满减的价格，y代表红包的价格。计算订单总价。
输入：
4
10 20 10 20
25 10
输出：
25
*/
#include <iostream>
using namespace std;
int main()
{
int n,a = 0,sum = 0;
int manjian,hongbao;
cin>>n;
for(int i = 0;i < n; i++){
cin>>a;
sum = sum + a;
}
cin>>manjian;
cin>>hongbao;
cout << sum - manjian - hongbao << endl;
return 0;
}
1.4 美团机器人招聘题2：定义以下三种单词是合法的:1.所有字母都是小写。例如: good。2.所有字母都是大写。例如。
3.第一个字母大写，后面所有字母都是小写。例如
。 现在小美拿到了一个单词，她每次操作可以修改任意一个字符的大小写。小美想知道最少操作几次可以使得单词变成合法的?C++/*小美定义以下三种单词是合法的:1.所有字母都是小写。例如: good。2.所有字母都是大写。例如:APP。
3.第一个字母大写，后面所有字母都是小写。例如:Alice。
现在小美拿到了一个单词，她每次操作可以修改任意一个字符的大小写。小美想知道最少操作几次可以使得单词变成合法的?
*/
#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
getline(cin, s);
int l = 0, h = 0;
for(int i = 0; i < s.size(); i++){
if(s[i] - 'a' >= 0)l++;
else h++;
}
int opt = min(l,h);
if((s[0] - 'a')<0)opt = min(opt,h - 1);
cout<<opt;
return 0;
}
1.5 美团机器人招聘题3：拿到了一个数组，她每次操作会将除了第x个元素的其余元素翻倍，一共操作了q次。请你帮小美计算操作结束后所有元素之和。
由于答案过大，请对1e9+7取模。
C++/*小美拿到了一个数组，她每次操作会将除了第x个元素的其余元素翻倍，一共操作了q次。请你帮小美计算操作结束后所有元素之和。
由于答案过大，请对1e9+7取模。
输入：
4 2
1 2 3 4
1 2
输出：
34
*/
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
int val,q,xi;
long sum=0;
const int MOD = 1e9 + 7;
cin >> n;
cin>>q;
vector<int> aa;
vector<int> bb;
for(int i = 0;i < n; i++){
cin>>val;
aa.push_back(val);
bb.push_back(val);
}
for(int i = 0; i < q; i++){
cin>>xi;
xi--;
for(int j = 0; j < n; j++){
if(j == xi)continue;
else{
bb[j] = bb[j] * 2 % MOD;
}
}
}
for(int i = 0; i < bb.size(); i++)sum+=bb[i];
std::cout<<sum % MOD;
return 0;
}
1.6 美团机器人招聘题4：求区间众数和
C++/*求区间众数和
第一行输入一个正整数n。第二行输入n个正整数，1<n<200000,1<=a<=2
输入
3
2 1 2
输出
9
*/
#include <cstdio>
#include <iostream>
#include <algorithm>
typedef long long LL;
const int N = 200010;
int n;
int a[N], tr[N * 2];
int sum[N];
int lowbit(int x) {
return x & -x;
}
void modify(int x, int k) {
for (int i = x; i <= 2 * n + 5; i += lowbit(i)) tr[i] += k;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
LL ans = 0;
modify(0 + n + 1, 1);
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1];
if (a[i] == 1) sum[i] += 1;
else sum[i] -= 1;
ans += query(sum[i] + n + 1) + (i - query(sum[i] + n + 1)) * 2;
modify(sum[i] + n + 1, 1);
}
printf("%lld", ans);
return 0;
}
1.7 美团机器人招聘题5：
C++#include<iostream>
#include<vector>
using namespace std;
const int N=200000;
void merge__(vector<int>& arr, vector<int>& tmp, int l, int mid, int r, int& ret) {
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (arr[i] > arr[j]) {
tmp[k++] = arr[j++];
ret += (mid - i + 1);
}
else {
tmp[k++] = arr[i++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= r) {
tmp[k++] = arr[j++];
}
for (k = 0, i = l; i <= r; ++i, ++k) {
arr[i] = tmp[k];
}
}
void merge_sort__(vector<int>& arr, vector<int>& tmp, int l, int r, int& ret) {
if (l >= r) {
return;
}
int mid = l + ((r - l) >> 1);
merge_sort__(arr, tmp, l, mid, ret);
merge_sort__(arr, tmp, mid + 1, r, ret);
merge__(arr, tmp, l, mid, r, ret);
}
int InversePairs(vector<int>& nums) {
// write code here
int ret = 0;
// 在最外层开辟数组
vector<int> tmp(nums.size());
merge_sort__(nums, tmp, 0, nums.size() - 1, ret);
return ret;
}
int main()
{
vector<int> q;
int n,a;
cin >> n;
int result;
for(int i=0;i<n;i++){
cin >>a;
q.push_back(a);
}
for(int i=0;i<n;i++){
q[i] = -q[i];
result = InversePairs(q);
cout << result<< ' ';
q[i] = -q[i];
}
return 0;
}
1.8美团删除数组问题小美有一个长度为 n 的数组 a1,a2,.·,an ，他可以对数组进行如下操作:
C++/*
问题描述：
小美有一个长度为 n 的数组 a1,a2,.·,an ，他可以对数组进行如下操作:
1.删除第一个元素 a1，同时数组的长度减一，花费为x
2.删除整个数组，花费为k*MEX(a)，其中MEX(a)表示a中未出现过的最小非负整数。例如[0,1,2,4]的 MEX为3。
小美想知道将 a 数组全部清空的最小代价是多少。
输入描述：
每个测试文件均包含多组测试数据。第一行输入一个整数T代表数据组数，每组测试数据描述如下第二行输入三个正整数：n,k,x
代表数组中的元素数量、删除整个数组的花费系数、删除单个元素的花费。第三行输入n个整数 a1, a2,...,an表示数组元素。
除此之外，保证所有的a之和不超过 2x105.
*/
/*
思路：动态规划+维护最小未出现的整数
dp[i]表示从i往后考虑的最小花费，最后的最小花费就是dp[0]和直接删除后续所有元素的最小值
对于删除后续所有的元素的选项，我们必须要知道mex是多少，可以在更新dp的过程中，用一个变量不断的更新当前的最小未出现的整数
虽然这里出现了两次循环的嵌套，但是并不会重置参数，因此复杂度是O(n)
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;
int main() {
int T;
cin >> T; // 读取测试数据组数
while (T--) {
long long n, k, x;
cin >> n >> k >> x;
vector<long long> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
// 动态规划数组dp[i]表示从i往后考虑的最小花费，最后最小花费就是dp[0]或者直接删除后续所有元素
vector<long long> dp(n + 1, LLONG_MAX);
dp[n] = 0;
int suffix_mex = 0;
set<int> vst;
for (int i = n-1; i >= 0; --i) {
vst.insert(a[i]);
while(vst.count(suffix_mex)){
suffix_mex++;
}
dp[i] = min(dp[i + 1] + x, k * suffix_mex);
}
// 输出最小花费
cout << dp[0] << endl;
}
return 0;
}
1.9大疆根据层序遍历字符串重建二叉树并找最大路径和
C++/*
问题描述：
题目描述:
二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次。该路径 至少包含一个节点，目不一定经过根节点。路径和 是路径中各节点值的总和，以先序遍历给定一个二叉树的根节点root，返回其最大路径和。
输入描述：
输入：[1,2,3,4,5]
输出：11
*/
#include <bits/stdc++.h>
using namespace std;
#define emp -1
int maxSum = 0;
struct Node{
int value;
Node* left;
Node* right;
};
Node* createNode(){
Node* root = new Node();
root->left = nullptr;
root->right = nullptr;
return root;
}
void createFullBT_DFS(Node *&root, vector<int> &numbers, int len, int i) {
if(i <= len) {
root->value = numbers[i - 1];
if(2 * i <= len && numbers[2 * i - 1] != emp) {
root->left = createNode();
createFullBT_DFS(root->left, numbers, len, 2 * i);
}
if((2 * i + 1) <= len && numbers[2 * i] != emp) {
root->right = createNode();
createFullBT_DFS(root->right, numbers, len, 2 * i + 1);
}
}
}
int maxGain(Node* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时，才会选取对应子节点
int leftGain = max(maxGain(node->left), 0);
int rightGain = max(maxGain(node->right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node->value + leftGain + rightGain;
// 更新答案
maxSum = max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node->value + max(leftGain, rightGain);
}
void preOrder(Node *root) {
if(root != NULL) {
cout << root->value << " ";
preOrder(root->left);
preOrder(root->right);
}
}
int main(){
string str = "[1,2,3,4,5]";
string str_update = str.substr(1, str.length()-2);
char* str_input = (char*)str_update.c_str();
vector<int> nums;
int val = 0;
while(*str_input != '\0'){
if(*str_input != ','){
val = val * 10 + (*str_input - '0');
}
else{
nums.push_back(val);
val = 0;
}
str_input++;
}
nums.push_back(val);
Node* root = createNode();
createFullBT_DFS(root, nums, nums.size(), 1);
// preOrder(root);
maxGain(root);
cout << maxSum <<endl;
return 0;
}
1.10一个完整的软件项目往往会包含很多由代码和文档组成的源文件可能需要按照依赖关系来依次编译每个源文件。
C++/*
问题描述：
题目描述:
一个完整的软件项目往往会包含很多由代码和文档组成的源文件。编译器在编译整个项目的时候，可能需要按照依赖关系来依次编译每个源文件。比如，A.cpp 依赖 B.cpp，那么在编译的时候，编译器需要先编译 B.cpp，才能再编译 A.cpp。 假设现有 0，1，2，3 四个文件，0号文件依赖1号文件，1号文件依赖2号文件，3号文件依赖1号文件，则源文件的编译顺序为 2,1,0,3 或 2,1,3,0。现给出文件依赖关系，如 1,2,-1,1，表示0号文件依赖1号文件，1号文件依赖2号文件，2号文件没有依赖，3号文件依赖1号文件。请补充完整程序，返回正确的编译顺序。注意如有同时可以编译多个文件的情况，按数字升序返回一种情况即可，比如前述案例输出为：2,1,0,3
输入例子1:
"1,2,-1,1"
输出例子1:
"2,1,0,3"
*/
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
string compileSeq(string input) {
//首先完成有向无环图的构建
//统计图中各节点的个数 并标记头节点为-1
//使用优先队列 按照先小后大的顺序遍历输出节点值
int len = input.size();
/*********构建有向无环图(指向关系)*********/
map<int, vector<int>> mp;//first为先 second为后， 也就是second依赖于first
string tmp;
int idx = 0;
for(auto& s:input){
if(s != ',')
tmp += s;
else{
mp[stoi(tmp)].push_back(idx++);
string().swap(tmp);//清空string
}
}
if(!tmp.empty())
mp[stoi(tmp)].push_back(idx++);
/**********统计各节点个数 并保存头节点***********/
vector<int> indexcount(len, 0);//统计各节点个数
priority_queue<int, vector<int>, greater<>> pq;//保存节点
for(auto& m:mp){
if(m.first == -1){
for(auto& a:m.second){
pq.push(a);
indexcount[a] = -1;
}
}else{
for(auto& a:m.second)
++indexcount[a];
}
}
/************根据指向关系遍历图 并按照优先队列输出结果********/
vector<int> ans;
while(!pq.empty()){
int node = pq.top();
pq.pop();//输出了就需要从优先队列中弹出
ans.push_back(node);
for(auto& m:mp[node]){
if(--indexcount[m] == 0)//如果该节点是最后一次在图中出现 则放入队列中
pq.push(m);
}
}
/***********输出结果************/
string res;
for(auto& i:ans){
res += to_string(i);
res.push_back(',');
}
if(!res.empty())
res.pop_back();
return res;
}
};
int main(){
Solution OnecompileSeq;
string res = OnecompileSeq.compileSeq("1,2,-1,1");
cout << res << endl;
return 0;
}
1.11并查集模板
C++/*
问题描述：
并查集模板
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 100; // 节点数量
int f[N];
int init() {
// 初始化
for (int i=0; i<N; i++)
f[i] = i;
}
int getFather(int x) {
// 查询所在团伙代表人
return f[x]==x ? x : getFather(f[x]);
}
int merge(int a, int b) {
// 合并操作
f[getFather(a)] = getFather(b);
}
bool query(int a, int b) {
// 查询操作
return getFather(a) == getFather(b);
}
int main() {
init();
merge(3, 1); // 3和1是亲戚
merge(1, 4); // 1和4是亲戚
cout << getFather(3) << endl; // 输出3的团伙代表人+换行
cout << query(3, 1) << endl; // 输出3和1是否是亲戚+换行
}
1.12有向无环图节点的所有祖先
C++/*
问题描述：
有向无环图中一个节点的所有祖先。
给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。
给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。
如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。
*/
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
vector<unordered_set<int>> anc(n); // 存储每个节点祖先的辅助数组
vector<vector<int>> e(n); // 邻接表
vector<int> indeg(n); // 入度表
// 预处理
for (const auto& edge: edges) {
e[edge[0]].push_back(edge[1]);
++indeg[edge[1]];
}
// 广度优先搜索求解拓扑排序
queue<int> q;
for (int i = 0; i < n; ++i) {
if (!indeg[i]) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v: e[u]) {
// 更新子节点的祖先哈希表
anc[v].insert(u);
for (int i: anc[u]) {
anc[v].insert(i);
}
--indeg[v];
if (!indeg[v]) {
q.push(v);
}
}
}
// 转化为答案数组
vector<vector<int>> res(n);
for (int i = 0; i < n; ++i) {
for (int j: anc[i]) {
res[i].push_back(j);
}
sort(res[i].begin(), res[i].end());
}
return res;
}
};
int main(){
Solution test;
int n = 8;
//[[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
vector<vector<int>> nums = {{0,3},{0,4},{1,3},{2,4},{2,7},{3,5},{3,6},{3,7},{4,6}};
vector<vector<int>> res = test.getAncestors(n, nums);
for(int i = 0; i < res.size(); i++){
for(int j = 0; j < res[i].size(); j++){
cout << res[i][j];
}
cout << endl;
}
return 0;
}
1.13滑动窗口找元素相加最接近某个值的，可以选择最多的元素数
c++/*
从数组中选择尽可能多的元素，只能连续选择，使得相加小于m，求最多可以选择几个数。输入为一个个数为n的数组和一个整数，输出为最多选择元素的个数。
*/
#include <iostream>
#include <vector>
using namespace std;
int maxConsecutiveElementsUnderSum(const std::vector<int>& nums, int m) {
int n = nums.size();
int max_count = 0; // 最多选择的元素个数
int current_sum = 0; // 当前窗口内元素的和
int left = 0; // 左指针
// 遍历数组，用右指针表示窗口的右端
for (int right = 0; right < n; ++right) {
current_sum += nums[right]; // 增加当前右指针对应的元素
// 当当前窗口和大于 m 时，收缩左边界
while (current_sum > m && left <= right) {
current_sum -= nums[left]; // 减去左指针的元素
left++; // 左指针右移
}
// 更新最多选择的元素个数
max_count = std::max(max_count, right - left + 1);
}
return max_count;
}
int main() {
vector<int> nums;
int n,m;
cin>>n>>m;
int val;
for(int i = 0; i < n; i++){
cin >> val;
nums.push_back(val);
}
int result = maxConsecutiveElementsUnderSum(nums, m);
cout << result << endl;
return 0;
}
1.14拼多多笔试1数组划分为k段，调整k段判断是否升序
c++/*
多多有一个长度为n的数组，依次采用如下策略对数组从小到大进行排序
1.将数组划分为k个非空子串(每个子串为原数组中连续数字组成的子序列)
2.调整k个子串的顺序，每个子串内元素顺序不变
3.将k个子串首尾相连，组成一个新的数组
以上策略不保证最终得到的数组有(单调递增)请你计算一下，对于给定的数组与划分数k，能否最终得到一个有序递增的序列
输入描述：
第一行一个数字T(T < 5)，代表测试用例个数
对于每组测试用例:第一行两个数字:n,k，代表数组长度与划分子串个数，0<k<n<1e5
第二行n个数字a1,a2,…,an，0≤|ai|;≤ 1e14，保证数组内元素各不相同
输出描述：
对于每个测试用例，如果能够得到有序序列，输出“Tue"(不含引号)，否则输出“False(不含引号)
示例：
输入：
3
5 3
8 12 7 -6 5
4 2
2 3 -6 4
5 5
10 6 8 -5 -10
输出：
True
False
True
思路 排序的同时也对原来的需要排序，然后判断块应该分割的次数，如果小于等于K则可以
*/
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
while(T--){
long long n, k;
cin >> n >> k;
vector<long long> arr(n);
for(auto &x : arr)cin >> x;
//Create a vector of pairs(value, original index)
vector<pair<long long, long long>> sorted_arr(n);
for(long long i = 0; i < n; i++){
sorted_arr[i] = {arr[i], i+1};//1-based indexing
}
// Sort the array based on values
sort(sorted_arr.begin(), sorted_arr.end());
// Count the number of blocks where indices are consecutive
long long m = 1;// At least one block
for(long long i = 1; i < n; i++){
if(sorted_arr[i].second != sorted_arr[i-1].second +1){
m++;
}
}
// If number of blocks <=k, it's possible
if(m <= k){
cout <<"True\n";
}
else{
cout<<"False\n";
}
}
}
1.15百度笔试时钟秒针转的圈数
c++/*
第一个的文字：小A的寝室里放着一个时钟。时钟有时针，分针，秒针三种指针。在某些时刻，时钟会记录下当前时间，格式为hh:mm:ss。
时钟上看不出日期，每天零点，三根指针都会归零。现在小A得到了一系列被记录的时间，且这些时间是按照先后顺序被记录的。
小A想让你算算，每两个时间点之间，秒针至少转了多少圈。注:一天有 24 个小时，1 小时有 60 分钟，1分钟有 60 秒，秒针一分钟转一圈。
输入描述：第一行一个整数 n(2 ≤n < 10e5)，代表时间序列中时间点的个数。第二行n个字符串，每个字符串代表一个时间点，格式为hh:mm:ss(0 ≤ hh< 24, 0≤ mm< 60, 0 ≤ ss < 60).
输出描述:n -1个数，第i个数表示第i到i十1时间点秒针转过的圈数。输出结果和答案的绝对误差或相对误差不超过 10e-5 即被认为正确。
*/
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <iomanip>
using namespace std;
// Helper function to convert time in "hh:mm:ss" format to total seconds from midnight
int timeToSeconds(const string& time) {
int hh = stoi(time.substr(0, 2));
int mm = stoi(time.substr(3, 2));
int ss = stoi(time.substr(6, 2));
return hh * 3600 + mm * 60 + ss;
}
int main() {
int n;
cin >> n;
vector<string> times(n);
// Input all time points
for (int i = 0; i < n; ++i) {
cin >> times[i];
}
// Calculate and print the number of full rotations of the second hand between consecutive time points
for (int i = 1; i < n; ++i) {
int t1 = timeToSeconds(times[i - 1]);
int t2 = timeToSeconds(times[i]);
// If t2 is smaller, it means the time passed to the next day
if (t2 < t1) {
t2 += 24 * 3600; // add 24 hours in seconds
}
int secondsDiff = t2 - t1;
double rotations = secondsDiff / 60.0; // calculate the full rotations
printf("%.*f", 10, rotations);
// cout << setprecision(10) << rotations << endl; // print the result
}
return 0;
}
1.16百度笔试2正整数A包含B表示按位或运算
c++/*
我们称正整数A包含B，当且仅当(A|B)= A, |表示按位或运算，即B中的所有为1的二进制位，在A中都为1。现在给定n个正整数Ai，请你从中选出尽量少的整数，使得所有Ai，都至少被一个你选出来的整数包含。显然任何一个数总是包含其自身，即选择全部的数必定为一组合法答案(但不一定是最少的)。
输入描述：
第一行一个正整数n，接下来一行n个整数，第i个整数表示Ai。0≤ Ai< 262144, 1 ≤n≤2x1e5
输出描述：
一行一个整数，表示至少需要选出几个数字。
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
unordered_set<int> uniqueSet;
// Read input and add to the set to remove duplicates
for (int i = 0; i < n; ++i) {
cin >> a[i];
uniqueSet.insert(a[i]);
}
// Convert set back to vector
vector<int> uniqueNumbers(uniqueSet.begin(), uniqueSet.end());
// Sort in descending order to apply the greedy strategy
sort(uniqueNumbers.rbegin(), uniqueNumbers.rend());
int selectedCount = 0;
vector<bool> covered(uniqueNumbers.size(), false);
// For each number, see if it is necessary to cover the others
for (size_t i = 0; i < uniqueNumbers.size(); ++i) {
if (!covered[i]) {
selectedCount++;
for (size_t j = i + 1; j < uniqueNumbers.size(); ++j) {
if ((uniqueNumbers[i] | uniqueNumbers[j]) == uniqueNumbers[i]) {
covered[j] = true;
}
}
}
}
cout << selectedCount << endl;
return 0;
}
1.17得物笔试1字符串操作变成另外一个字符串
c++/*
c++实现以下问题：
小红一开始有 s串，s串是空串。她想获得一个字符串 t。
小红有四种操作:
1.在s串的开头添加一个字符，花费为p。
2.在s串的末尾添加一个字符，花费为p。
3.在s串的开头添加一个s串的子串，花费为 q。
4.在s串的末尾添加一个s串的子串，花费为 q。
每次操作都是基于当前的s串，有对应的花费。
小红想知道从s串变到t串的最小花费，你能帮帮她吗?
输入描述:
第一行输入一个字符串t，仅包含小写字符。
第二行输入两个正整数 p,q。
示例 1
输入
bbcabc
3 1
输出
11
说明：
s串先变成"c”,目前花费为3.
s串变成"bc",目前花费为6。
s串变成”bca”,目前花费为9.
s串变成"bcabc",目前花费为10.
s串变成“bbcabc",目前花费为11.
因此输出11。
*/
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main() {
// 读取输入
string t;
cin >> t;
int p, q;
cin >> p >> q;
int n = t.size();
vector<int> dp(n + 1, INT_MAX); // dp数组，初始为最大值
dp[0] = 0; // 空串到空串的花费为0
// 进行动态规划计算
for (int i = 1; i <= n; ++i) {
// 操作1和操作2: 添加一个字符
dp[i] = dp[i - 1] + p;
// 操作3和操作4: 添加一个子串
for (int j = 0; j < i; ++j) {
// 如果t的子串t[j:i]可以在s中形成，花费为q
string sub = t.substr(j, i - j);
if (t.substr(0, j).find(sub) != string::npos || t.substr(0, i - sub.size()).find(sub) != string::npos) {
dp[i] = min(dp[i], dp[j] + q);
}
}
}
// 输出最小花费
cout << dp[n] << endl;
return 0;
}
1.18 虹软笔试温控报警程序寄存器操作移位
c++/*
描述:编写一个温控报警程序，根据给定的三个32位寄存器的值reg1、reg2、reg3，以及报警调值 alarm 进行判
断，其中，reg1的第八位为状态位，状志位置1，表示传感器失效，reg2的0~3位为高位，reg3 的第 24~31位为
:位。温度寄存器的精度为0.1，范围为[-204, 204],需要计算温度的值，并判断温度是否大于报警调值，如果大于报
警闯值，则输出tue，否则输出false。状态位置1，直接输出ture
输入:reg1、reg2、reg3 的值(无符号32位整数，16进制表示)，以及报警阈值alam(32 位有符号整数，10进
制表示)。输出:布尔值，表示温度是否大于报警值。
输入:88 18000A1F 12345678 120
解释:根据给定的奇存器值，可以提取温度的高位为0x，低位为0x12，计算得到温度值为181.8、由于温度值大于输出:tue报警阈值 120，因此输出 tue.
输入:88 12000a1a df12fe2d 120解释;根据给定的寄存器值，可以提取温度的高位为0xa，低位为0xd，计算得到温度值为74.3。由于温度值小于编出:false报警國值 120，因此输出false。
*/
#include <bits/stdc++.h>
using namespace std;
int main() {
unsigned int reg1,reg2,reg3;
cin >> hex >> reg1 >> hex >> reg2 >> hex >> reg3;
int alarm;
cin >> dec >> alarm;
if(reg1 & 0x100){
cout << "true" << endl;
cout << "111" << endl;
}
else{
reg2 &= 0x0f;
reg3 &= 0xff000000;
reg3 = reg3 >> 24;
reg2 = reg2 << 8;
unsigned int tmp = (reg2 + reg3);
unsigned int tmp2 = tmp - 0x7f8;
if(tmp2 > alarm*10)cout << "true" << endl;
else cout << "false" << endl;;
}
return 0;
}
1.19华为云笔试软件安装顺序
c++#
# wukun 华为云笔试
# 软件安装工具
# 有一个比较复杂的软件系统需要部署到客户提供的服务器上。该软件系统的安装过程非常繁琐，为了降低操作成本，需要开发一个工具实现自动化部署。软件的安装过程可以分成若干个小步骤，某些步骤间存在依赖关系，被依赖的步骤必须先执行完，才能执行后续的安装步骤。满足依赖条件的多个步骤可以并行执行。请你开发一个调度程序，以最短的时间完成软件的部署。
# 输入：
# 第一行:总步骤数 N(0<N<=10000)
# 第二行:N个以空格分隔的整数，代表每个步骤所需的时间。该行所有整数之和不大于int32
# 第三行开始的N行:表示每个步骤所依赖的其它步骤的编号(编号从1开始，行号减2表示步骤的编号)，如果依赖多个步骤，用空格分隔。-1表示无依赖测试用例确保各个安装步骤不会出现循环依赖。
# 输出：
# 1个数字，代表最短执行时间。
# 样例1
# 输入:4
# 6 2 1 2
# -1
# 1
# 3
# 输出:9
# 样例2：
# 输入：4
# 1 2 3 4
# 2 3
# 3
# -1
# 1
# 输出：10
from collections import defaultdict, deque
def func(N, step_times, dependencies):
# 构建图和入度计数
graph = defaultdict(list)
in_degree = [0] * N
time_to_complete = [0] * N
# 填充依赖关系
for i in range(N):
for dep in dependencies[i]:
if dep != -1:
graph[dep - 1].append(i)
in_degree[i] += 1
# 使用队列处理入度为0的步骤
queue = deque()
for i in range(N):
if in_degree[i] == 0:
queue.append(i)
time_to_complete[i] = step_times[i]
# 进行拓扑排序
while queue:
current = queue.popleft()
current_completion_time = time_to_complete[current]
for neighbor in graph[current]:
in_degree[neighbor] -= 1
time_to_complete[neighbor] = max(time_to_complete[neighbor], current_completion_time + step_times[neighbor])
if in_degree[neighbor] == 0:
queue.append(neighbor)
return max(time_to_complete)
if __name__ == "__main__":
# 输入示例
N = int(input())
step_times = list(map(int, input().split()))
print(step_times)
dependencies = []
for _ in range(N):
deps = list(map(int, input().split()))
dependencies.append(deps)
# 输出最短执行时间
print(func(N, step_times, dependencies))
1.20经纬恒润笔试1-n整数十进制1出现的次数
c++/*
问题描述：
输入一个整数n，求1~n这n个整数的十进制表示中1出现的次数
例如，1~13中包含1的数字有1、10、11、12、13因此其出现6次
*/
#include <iostream>
using namespace std;
// 函数用于计算从1到n中'1'出现的次数
int countDigitOne(int n){
int count = 0;
long long factor = 1;// 用来表示当前分析的位(个位、十位、百位等)
while(n / factor > 0){
long long lower= n - (n / factor) * factor;// 当前位以下的数字
long long current=(n / factor) % 10;
long long higher=n / (factor * 10);
if(current == 0){
count += higher * factor;
}
else if(current == 1){
count += higher * factor + lower + 1;
}
else {
count +=(higher + 1) * factor;
}
factor *= 10;// 进入到下一位
}
return count;
}
int main(){
int n;
cin >> n;
cout<< countDigitOne(n)<<endl;
return 0;
}
1.21小米笔试最多可以装入多少件行李
c++/*
小米共有m个箱子用于打包行李，每个箱子承重为w。现有n件行李排成一行，重量为ai，
小米将从左向右开始打包。如果当前箱子装入该行李不会超重则优先装在当前箱子，
如果会超重则将当前箱子密封，将该行李装入下一个新的箱子中。小米更偏爱放在右边的行李，
所以为了能装入更多行李，他会选择从最左边开始连续地舍弃一些行李，以保证剩下的行李可以全部装完。
现在想知道，他最多可以装入多少件行李?
输入：
5 2 8
6 3 2 5 3
输出：
4
*/
#include <stdio.h>
int main(){
int n, m;
long long w;
scanf("%d %d %lld",&n,&m, &w);
long long weights[n];
for(int i=0;i<n; ++i)scanf("%lld",&weights[i]);
int boxcount =1;
long long currentweight =0;
int rightIndex=n-1;
while(rightIndex>=0){
if(currentweight + weights[rightIndex]<=w){
currentweight += weights[rightIndex];
} else {
boxcount++;
currentweight = weights[rightIndex];
}
rightIndex--;
if(boxcount>m){
rightIndex++;
break;
}
}
int itemsPacked=n - (rightIndex + 1);
printf("%d\n",itemsPacked);
return 0;
}
1.22滴滴笔试无向图依次删除节点求连通块的个数
c++/*
小A正在玩游戏，在游戏中一共有n个不同星球，星球间共有m条双向航道，小A的任务是摧毁这些星球。若有多个星球间两两可达，则我们称它们属于同一个联盟。特别的，若一个星球与其他星球间都没有航道，则也称其为一个联盟。小A将按照星球的编号从小到大依次摧毁各个星球，当一个星球被摧毁后，与之相连的航道也将相继被摧毁，现在小A想知道在每个星球被摧毁时还剩下多少个联盟。不同星球间可能有多条航道，但每条航道连接的两个星球必然不同。上述题意可以被简化为，给定n个点，m条边的无向图，按照编号大小依次删去各个节点，请问在每个节点被删去时，还剩下多少个连通块。保证给定图无自环，但可能有重边，
输入描述
第一行两个正整数n,m，表示星球数与航道数。接下来m行，每行2个正整数u,v，表示两星球间有一条航道。1<n,m<5e4
输出描述
输出一行n个正整数，表示答案。
样例输入
5 6
1 2
2 3
3 1
4 5
5 1
2 4
样例输出
1 2 1 1 0
*/
#include <stdio.h>
#define MAXNUM 1000
int Group[MAXNUM]; //记录图中节点是否被访问过
int dist[MAXNUM][MAXNUM]; //通过邻接矩阵保存图
void DFS(int i, int n);
int main()
{
int n, m, p, q, k = 0;
for (int i = 0; i < MAXNUM; i++)
{
for (int j = 0; j < MAXNUM; j++)
dist[i][j] = 0; //初始化邻接矩阵，初始值为0
Group[i] = 0; //同上
}
scanf("%d%d", &n, &m); //获取图的节点数n，和边数m
for (int i = 0; i < m; i++)
{
scanf("%d%d", &p, &q);
dist[p-1][q-1] = 1; //如果节点1和节3相连 则另dist[1][3]和dist[3][1]的值为1
dist[q-1][p-1] = 1;
}
for(int zz = 1; zz <= n; zz++){
for(int j = 1; j <= n; j++){ // 删除节点zz相连的边
p = zz;
q = j;
dist[p-1][q-1] = 0;
dist[q-1][p-1] = 0;
}
for (int i = 0; i < MAXNUM; i++) // 清零
{
Group[i] = 0;
}
for (int i = 0; i < n; i++)
{
if (Group[i] != 1)
{
DFS(i, n);
k++; //执行一次DFS就是k的值自增1,
}
}
printf("%d", k - zz); // k为删除边但没有删除节点的连通数 zz表示每次删除一个节点
k = 0;
}
return 0;
}
void DFS(int i,int n)
{
Group[i] = 1;
for (int j = 0; j < n; j++)
{
if (dist[i][j] == 1)
if (Group[j] != 1)
DFS(j, n);
}
}
1.23华为走迷宫防护服问题
c++/*
c++实现以下问题：
有一个 N x N 大小的迷宫。初始状态下，配送员位于迷宫的左上角，他希望前往迷宫的右下角。配送员只能沿若上下左右四个方向移动，从每个格子移动到相邻格子所需要的时间是 1个单位，他必须用最多 K 个(也可以少于 K 个)单位时间到达右下角格子。迷宫的每个格子都有辐射值，配送员必须穿着防护能力不低于相应辐射值的防护服，才能通过该格子。他希望知道，防护服的防护能力最少要达到多少，他才能顺利完成任务。注意:配送员需要通过迷宫的左上角和右下角，因此防护服的防护能力必须大于等于这两个格子的辐射值。
解答要求:
时间限制: C/C++1000ms,其他语言:2000ms内存限制: C/C++256MB,其他语言:512MB
输入:
前两行各包含一个正整数，分别对应 N 和 K后 N 行各包含 N 整数，以空格分隔，表示地图上每个位置的辐射值,2≤N≤100。 K≥2N-2，以保证题目有解。所有辐射值都是非负整数，绝对值不超过 1e4
输出:
一个整数，表示配送员穿着防护服的最低防护能力。
样例1
输入:
2
2
1 3
2 1
输出:2
解释:配送员可以选择通过左下角(辐射值为2)的路线，耗费2单位时间。
样例2
输入:
5
12
0 0 0 0 0
9 9 3 9 0
0 0 0 0 0
0 9 5 9 9
0 0 0 0 0
输出:3
解释:最优路线:往右2格，往下2格，往左2格，往下2格，往右4格，耗费12单位时间，经过格子的最大辐射值为3。
另外，在地图不变的情况下，如果K=16，输出为0;如果K=8，输出为5。
*/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = 1e9; // 定义一个足够大的值表示不可达
int N, K;
vector<vector<int>> radiation;
// 四个方向的移动
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
// 判断是否可以在指定的防护能力下从 (0,0) 到 (N-1,N-1)
bool canReach(int limit) {
if (radiation[0][0] > limit || radiation[N-1][N-1] > limit) {
return false;
}
vector<vector<bool>> visited(N, vector<bool>(N, false));
queue<pair<int, int>> q;
q.push({0, 0});
visited[0][0] = true;
int time = 0;
while (!q.empty()) {
int qsize = q.size();
if (time > K) return false; // 时间超过 K
while (qsize--) {
int x = q.front().first;
int y = q.front().second;
q.pop();
if (x == N-1 && y == N-1) {
return true; // 成功到达终点
}
for (int i = 0; i < 4; ++i) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < N && ny >= 0 && ny < N && !visited[nx][ny] && radiation[nx][ny] <= limit) {
visited[nx][ny] = true;
q.push({nx, ny});
}
}
}
++time; // 每次扩展一层，时间增加
}
return false; // 没有在 K 时间内到达终点
}
int main() {
// 读入 N 和 K
cin >> N >> K;
radiation.resize(N, vector<int>(N));
// 读入迷宫的辐射值
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
cin >> radiation[i][j];
}
}
// 二分查找防护能力
int low = 0, high = 1e4, ans = INF;
while (low <= high) {
int mid = (low + high) / 2;
if (canReach(mid)) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
// 输出结果
cout << ans << endl;
return 0;
}
DPDK相关知识
1.概念
DPDK（Data Plane Development Kit）是一个由Intel开发的开源软件库，它提供了一系列用于快速数据包处理的工具和驱动程序。VPP（Vector Packet Processing）则是由思科开发的高性能、模块化、可扩展的网络数据包处理框架。结合DPDK和VPP可以实现高性能的网络功能，如防火墙、路由器、负载均衡器等。 DPDK与VPP的结合
DPDK提供了底层的数据包处理加速能力，而VPP则在此基础上提供了丰富的网络功能。VPP运行在用户空间，支持多种收包方式，常用的是DPDK。VPP平台可以用于构建任何类型的数据包处理应用程序，它的架构允许通过插件的形式轻松扩展新功能。
- VPP: 高性能、模块化、可扩展的网络数据包处理框架
- OvS: open virtual switch 开源的虚拟交换机，旨在通过支持可编程扩展来实现大规模的网络自动化。
- DDOS：分布式拒绝服务攻击(英文意思是Distributed Denial of Service，简称DDoS)是指处于不同位置的多个攻击者同时向一个或数个目标发动攻击，或者一个攻击者控制了位于不同位置的多台机器并利用这些机器对受害者同时实施攻击。由于攻击的发出点是分布在不同地方的，这类攻击称为分布式拒绝服务攻击，其中的攻击者可以有多个。
- SDN: SDN字面意思是软件定义网络，其试图摆脱硬件对网络架构的限制，这样便可以像升级、安装软件一样对网络进行修改，便于更多的APP（应用程序）能够快速部署到网络上。
- 多队列网卡：一个网卡有多个接收通道并可能每个通道对应一个cpu中断
2.面向的岗位
面向的岗位有：网络工程师、存储网络工程师、SDN工程师（虚拟网络）
3. 七层网路模型
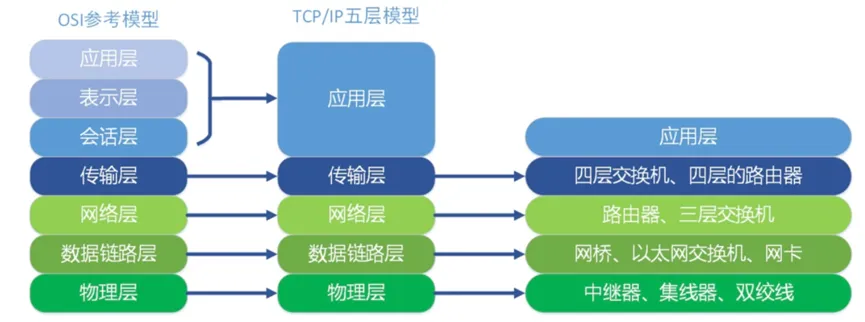
4.dpdk主要学习的东西
-
网络协议栈：arp地址解析协议，根据ip地址获取物理地址、ethernet以太网协议 ip icmp用于验证网络是否畅通，比如常用的ping命令 udp tcp
-
组件：mp多核中间的接口、acl（Access Control List）访问控制列表，是由多条“deny|permit”（拒绝|允许）语句组成，每一条都是一条规则，用于控制网络流量的进出。、KNI(Kernel Net Interface)是DPDK为用户态和内核协议栈交互提供的一种机制。本质上就是在内核注册一个虚拟网口，使用队列机制和用户态进行报文交换，和其他虚拟口的实现差不多。Timer定时器、bpf、mbuf/mempool
-
经典项目：dns、网关getway、nat网络地址映射、firewall防火墙、switch交换机、pktgen能够以10Gbit的线速率生成64字节帧的流量，并且可以作为发送器或接收器进行线速操作。
-
dpdk框架：vpp（c/c++）、ovs、nff-go(golang )、snabb(lua)、spdk(c)
-
dpdk源码：内核驱动（igb_uio、vdio、kni）、内存（mbuf、mempool）、协议（ipsec、bpf、pci、flow_classify）、虚拟化（vhost、virtio）、cpu(affinity侵和性把两个逻辑内核(CPU core)模拟成两个物理芯片、rcu(Read-copy update)、schedule)、安全（security、cryptodev、compresseddev）、性能（吞吐量bps、拆链和建链pps、并发、时延、丢包率）、测试方法（测试用例、vpp的sandbox、perf3灌包、rfc2544）、测试工具（perf3、trex、testpmd、pkegen-dpdk）
-
dpdk环境搭建
bashexport RTE_SDK=/home/zzw/share/dpdk-stable-19.08.2
export RTE_TARGET=x86_64-native-linux-gcc
5.windows向指定的网卡添加路由
- 查看网络信息找到网卡的Idx：netsh i i show in
- 添加：netsh -c i i add neighbors 19 192.168.0.106 00-0c-29-6b-32-b2
- 查看是否有相应的路由：arp -a
6.网络协议栈数据格式
- 以太网(位于数据链路层)数据帧格式：目的地址(6Byte)+源地址(6Byte)+类型(2Byte)+数据(46~1500Byte)+帧校验序列(4Byte)。其中地址为MAC地址、类型表示上层用的什么协议。
- TCP协议(位于传输层)，头部+数据部分，头部如果没有可选项的话固定是20个字节：源端口号(16b)+目标端口号(16b)+序列号(32b)+确认号(32b)+首部长度(4b)+保留位(6b)+控制位(6b)+窗口大小(16b)+校验和(16b)+紧急指针(16b)+可选项(0-40Byte)。序列号和确认号用于保证消息传输完整性，在TCP发送一个数据包时，会将这个数据包放到重发队列中，同时启动定时器，如果收到了这个包的确认消息，便将这个数据包从队列中删除。如果计时器超时，则重新发送该数据包。序列号保证所有数据按照正常顺序重组。窗口大小是在发送数据前，设备间协商以最小单位发送数据。三次握手：A发送连接+B响应并发起连接+A回应。四次挥手：A请求断开+B确认信息+B请求断开+A收到请求。
- UDP协议(位于传输层)，8Byte头部+数据。头部为：源端口(2B)+目的端口(2B)+UDP长度(2B)+UDP校验和(2B)。常见的UDP应用：TFTP协议、DNS协议、NTP协议、DHCP协议。
- ICMP协议(位于网络层和传输层之间)是网络控制消息协议，在传输ICMP协议时先封装ICMP头部，在封装IP头部，再交给数据链路层：
- ip(位于网络层)数据帧格式：固定部分20Byte+可选部分0-40Byte(一般没有)。固定部分的20个Byte分为4部分，每个部分4Byte。具体为：版本(4b)+固定部分长度(4b)+优先级与服务类型(8b)+总长度(16b)+标识符(16b)+标志(3b)+段偏移(13b)+TTL(8b)+协议号(8b)+固定部分校验和(16b)+源地址(32b)+目的地址(32b)。其中版本表示ipv4还是ipv6、总长度表示固定部分和可选部分总长、标志段偏移是将拆开的数据包进行组合、TTL是生命值经过一台路由器就减一、协议号1表示ICMP协议6表示TCP协议7表示 是UDP协议。
- arp协议(位于网络层)，基于目标IP获得目标的MAC地址，从而完成数据帧的二层头部封装，实现消息的快速转发。数据帧共28个字节：硬件类型(2B)+协议类型(2B)+硬件地址长度(1B)+协议地址长度(1B)+OP(2B)+发送端以太网地址(6)+发送端ip地址(4)+目的地以太网地址(6)+目的ip地址(4)。
7.协议栈架构设计优化
接收到数据后放到buffer队列里面，发送的时候从buffer队列里面取。要用两个ringbuffer，开线程去处理。（分层分离架构思想）
ring数据结构
三个线程夹两个ring_buf
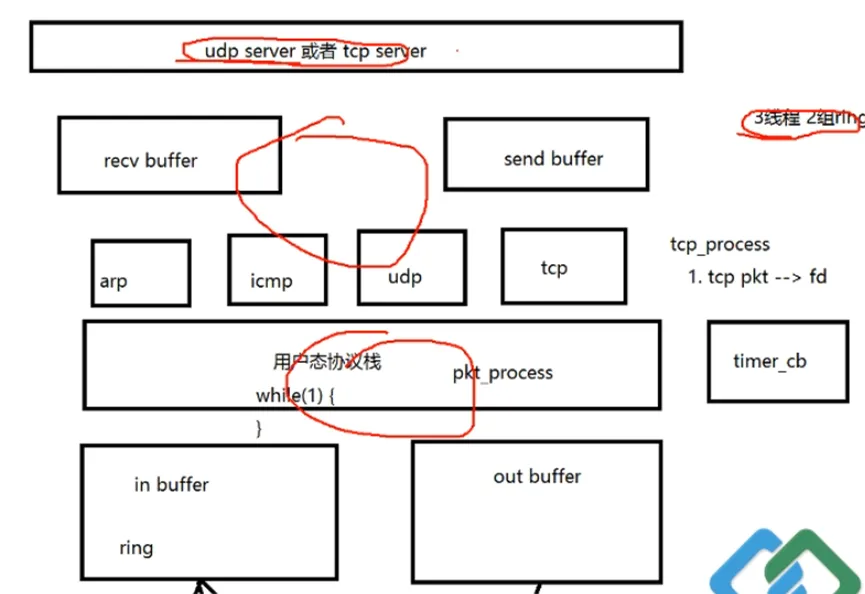
8.一些网络的命令
- 抓某个网卡的xxx包：tshark eth0 xxx
- 测试dns性能：dnsperf
9.VPP: 高性能、模块化、可扩展的网络数据包处理框架
9.1概念：
- 数据面：所有产生的数据
- 控制面：数据分发给谁这种控制
- Vpp的开发为了简化协议栈控制栈相当于一个包，vpp的开发就是开发vpp plugin，开发好的产品以插件的形式存在vpp之上。写plugin和写驱动模块类似。每个plugin有多个node，每个node可以作为一个小功能，比如vpn,ddos攻击等。
- Vpp的作用：1.为数据面的开发提供了完整的数据开发方案。2.以plugin和node组成，是可拆卸的。
- Vpp的缺陷：1.不带持久化。
开发plugin的流程：1.init_plugin：将plugin插入到vpp框架中。2.set_command：设置plugin命令，以便在vpp中调用这个命令准备启动这个plugin。 3.function：每个数据来的时候，plugin要执行的操作。
Linux内核精讲
1.linux系统概括
1.操作系统的结构
2.操作系统的工作方式:
- 把操作系统从用户态 切换到 内核态(用户应用程序 到 内核的流程)
- 实现操作系统的系统调用(操作系统服务层)
- 应用操作系统提供的底层函数，进行功能实现
- 操作系统的驱动结构
- 退出后从内核态切换到用户态
3.操作系统内核中各级模块的相互关联
- Linux内核的整体模块:进程调度模块 、内存管理模块、文件系统模块、进程间通信模块、驱动管理模块
- 每个模块间的关系(互相调用)
- 内存管理和驱动管理模块 虚拟内存的缓存和回存机制
- VFS 虚拟文件系统 把硬件当成文件来进行使用
4.操作系统结构的独立性
- 管理层，只负责管理。
- 实现层，负责具体代码实现。
5.高低版本的内核之间的区别：
- 多的是内核驱动的种类，内核驱动的管理模式并没有巨大的改变(一段时间3个阶段的跳段 零散型 分层型 设备树)。
- 进程的调度算法发生了改变，进程的管理方式并没有巨大的改变。
2.Linux中断机制
分类：硬件中断和软件中断；
linux内核0.11版本：
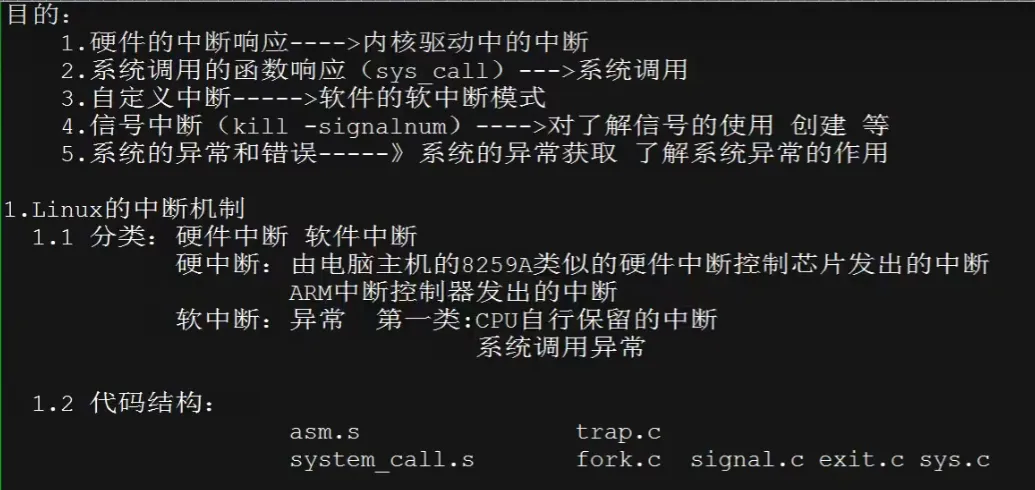
中断的工作流程(入栈 执行 出栈)：
- CPU工作模式的转化(arm有7种工作模式，快中断、慢中断···)。
- 进行寄存器的拷贝和压栈，保存当前上下文。
- 中断异常向量表种找到对应的中断向量。
- 保存正常运行的函数返回地址。
- 调转到对应的中断服务函数上运行。
- 进行模式复原以及寄存器的复原。
- 跳转回正常工作的函数地址继续运行。
3.进程管理
1.进程的运转方式：
jiffies：系统滴答，CPU内部有一个RTC时钟，会在上电的时候调用mktime函数算出从1970年1月1日0时开始到当前开机点所过的秒数。给mktime函数传来的时间结构体是由初始化时从rtc或者cmos中读出的参数，转化为时间存入全局变量中，并且会为jiffies所用。
jiffies是系统的一个滴答，一个滴答是10ms。每个滴答引发一个中断：
- 首先进行jiffies自加；
- 调用do_timer函数：
- 计算用户/内核运行时间；
- 判断定时器链表中有没有事件满足，如果有就执行；
- 事件片调度，counter最大的进程先执行，执行完所有进程后进行新一轮的时间片分配(0.11版本内核是优先级时间片轮转调度算法)；
2.如何进行创建一个新的进程
前置知识：
task_struct进程结构体(状态、时间片、优先级、tss结构体等；)：
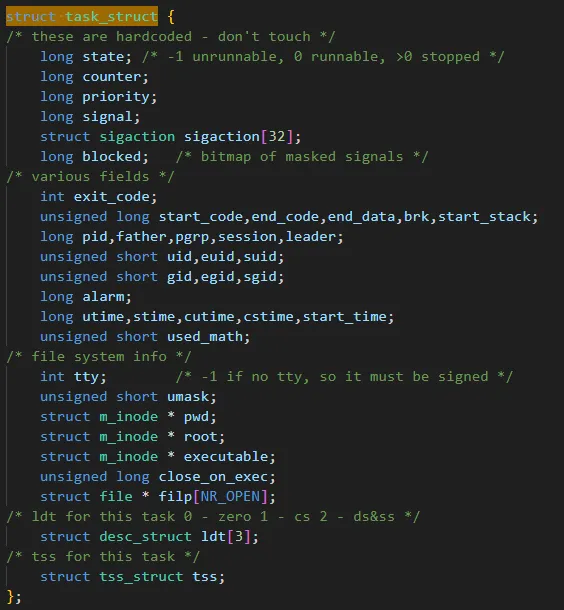
内存：
- LDT(局部描述符)段：代码段+数据段；
- TSS段：每个进程都有这样一个结构体，用于保存当前进程寄存器的值和结果；
- 堆栈：栈存放局部变量，向下生长；堆由用户分配释放；
上电进行一些初始化之后会执行init/main.c中的main函数，里面进行内存的拷贝(引导)、内存初始化、trap初始化、块设备驱动初始化、字符设备驱动初始化、调度初始化(初始化task链表)、软盘初始化，然后转移到用户态，因为此处不能被抢占，进程在内核态运行是不能被抢占的。然后创建0号进程，进程执行打开标准输入/输出/错误控制台，然后再创建1号进程打开/etc/rc文件，并执行shell(后面用另外一种方式又打开了一下避免没有被打开)。最后运行for(;;) pause();在没有其他进程运行时，运行0号进程。
进程的创建是系统的调用(中断)：
给当前要创建的进程分配一个进程号find_empty_process()。然后就是对0号进程或者当前进程的task_struct和栈堆复制copy_process()。
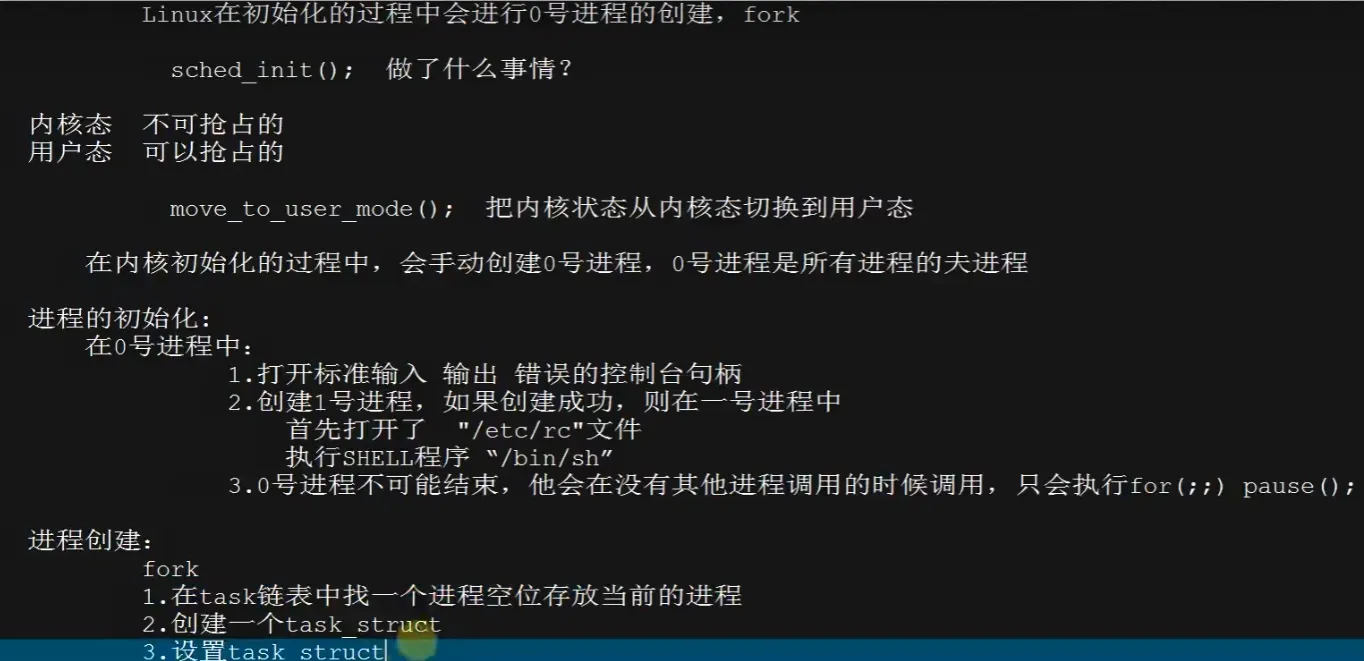
3.进程调度
进程状态：
调度代码(优先级时间片轮转调度算法)：
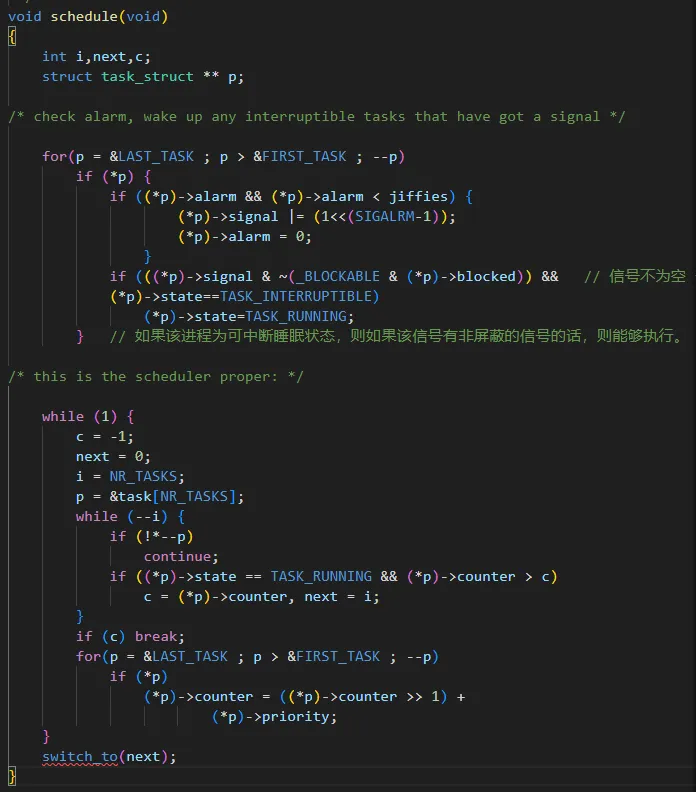
进程切换switch_to():
- 将需要切换的进程赋值给当前进程指针；
- 进行进程的上下文切换(切换tss段为新进程的值+新进程堆栈的值)；
sleep_on() // 休眠任务链表，等待资源
wake_up() // 从不可中断状态变为运行状态
4.进程的退出/销毁
do_exit销毁函数释放进程的代码段和数据段和堆栈段；- 关闭进程打开的所有文件，对当前的目录和i节点进行同步(文件操作)；
- 如果当前要销毁的进程有子进程，那么就让1号进程作为新的父进程(init进程创建的)；
- 如果当前进程是一个会话头进程，则会终止会话中的所有进程;
- 改变当前进程的运行状态，变成TASK ZOMBIE僵死状态，并且向其父进程发送SIGCHLD信号。
- 父进程在运行子进程的时候 一般都会运行wait waitpid这两个函数(父进程等待某个子进程终止),当父进程收到SIGCHLD信号时父进程会终止僵死状态的子进程;
- 首先父进程会把子进程的运行时间累加到自己的进程变量中;
- 把对应的子进程的进程描述结构体进行释放，置空任务数组中的空槽;
内核代码：
kill信号：
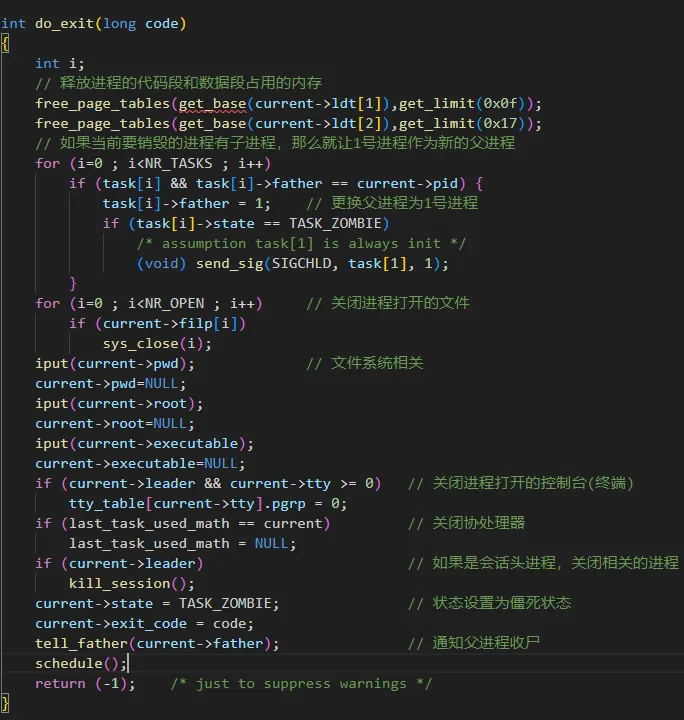
5.进程间通信IPC
- 管道，单向通信，是内存的数据，是看不见的，无法根据文件系统查看。
- 命名管道，单向通信，相当于一个文件，文件系统可以看到。
- 消息队列，属于内核的一个组件，进程A把消息提交给消息队列，通过内核通知把消息通知到进程B。
- 信号量，父子进程之间通信的，只作为一个flag，一个标识。
- 共享内存，两个进程共享一块内存，共同使用一个指针地址指向该块内存。
4.Linux操作系统的引导
BIOS/Bootloader:
由PC机的BIOS(0xFFFFO是BIOS存储的总线地址)把bootsect从在磁盘拿到了内存中的0x7c00地址，并且进行了一系列的硬件初始化和参数设置。
bootsect.s：磁盘引导块程序，在磁盘的第一个扇区中的程序(0磁道 0磁头 1扇区)，被BIOS加载到0x7c00地址后，自己将自己剪切到0x9000地址处。
作用:首先将后续的setup.s代码从磁盘中加载到紧接着bootsect.s的地方 在显示屏上显示loading system 再将system(内核代码)模块加载到0x1000的地方最后跳转到setup.s中去运行。
setup.s:解析BIOS/BOOTLOADER传递来的参数（光标位置/显存大小/显示参数/硬盘参数/根文件系统），设置系统内核运行的LDT和IDT(中断描述符寄存器)和GDT全局描述符寄存器。设置中断控制芯片，进入保护模式运行，跳转到system模块的最前面的代码运行（head.s）。
head.s:加载内核运行时的各数据段寄存器，重新设置中断描述符表，开启内核正常运行时的协处理器资源，设置内存管理的分页机制，跳转到main.c开始运行。
main.c:
上电进行一些初始化之后会执行init/main.c中的main函数，里面进行内存的拷贝(引导)、内存初始化、trap初始化、块设备驱动初始化、字符设备驱动初始化、调度初始化(初始化task链表)、软盘初始化，然后转移到用户态，因为此处不能被抢占，进程在内核态运行是不能被抢占的。然后创建0号进程(init()函数)，进程执行打开标准输入/输出/错误控制台，然后再创建1号进程打开/etc/rc文件，并执行shell(后面用另外一种方式又打开了一下避免没有被打开)。最后运行for(;;) pause();在没有其他进程运行时，运行0号进程。
init()函数：
操作系统的移植过程：
- 进行操作系统初始化的适配，让main能在板卡上跑起来(设置内存分配、硬件初始化用到的参数)；
- 进程驱动的移植；
总结:
- machine desc结构体，用于linux做设备板子的识别结构体，这些结构体被限定在了内存的某一片区域。
- 并且通过UBO0T传过来的参数进行该结构体的配置(通过检索taglist(存放硬件参数)的方式来设置)。
- 并且在移植Linux的时候 也要对结构体的变量进行赋值。
- 并且在之后的启动或其他函数中对该结构体的变量进行调用。
硬件的信息存放在machine_desc结构体中。
3.x版本内核的引导过程从以下三个角度分析：
- 内核如何进行多平台的适配，在内核中是如何认识这些板子的?结构体machine_desc。
- 内核启动的整体流。
- 认识一种高效的编程结构(代码段)。
链接脚本：vmlinux.lds.S指定了代码段。
宏定义：#define MACHINE_START(_type, _name) xxxx,为了从代码段中获得硬件架构信息。
结构体machine_desc，用于Linux做设备板子的识别结构体，这些结构体被限定在了内存的某一块区域，并且通过UBOOT传过来的参数进行该结构体的配置，并且在移植Linux的时候，也要对结构体的变量进行赋值，并且在之后的启动或其他函数中对结构体的变量进行调用。
lookup_processor_type_data
__mmap_switched:将旧的地址转化为虚拟地址(代码重定义)。
setup_arch:创建CPU指令集描述结构体、从指定的内存中获取到该描述结构体、将获取到的GPU名字赋值给一个全局变量、使用当前函数进行UBOOT的taglist的参数解析、找到一个移植Linux时写的最适合的machine_desc结构体，并且返回。
static noinline int init_post(void)：系统运行的第一个应用程序(根文件系统的挂接)。
5.Linux文件系统
概念：是磁盘管理的目录、是Linux中操作所有硬件设备的方式、系统的功能机制。
也是一个应用程序，Linux内核初始化之后，运行的第一个应用程序。
文件系统作用：
- 提供磁盘管理服务；
- glibc设备节点，就是mknod挂载硬件设备的驱动；
- 配置文件/etc/init.d/rcS，配置了开机运行什么软件，载入什么界面，执行什么命令；还有/sys/中开机要挂载的设备节点，eg: USB、光驱等。
- 应用程序shell命令(所有shell命令都在文件系统中)；
Android就是Linux多了个文件系统，实际上是多了lib和framework，包括glibc、OpenGL图形化库、media_framework媒体框架库、虚拟机、架构代码(对多种服务进行封装)。
busybox文件系统：
new_init_action()
run_actions()
__setup_param()
UBOOT传入了很多的参数，tagglist，被解析为多个setup段，存放在.init.setup的代码段中，形式为CMD字符串和命定对应的处理函数。在两个函数obsolete_checksetup(处理early为0的)和do_early_param(处理early不为0的)中进行了所有存放在.init.setup代码段的命令执行。针对各种setup段的CMD进行全局变量的赋值。
内核启动文件系统后，文件系统的工作流程：
内核启动的第一个应用程序是根文件系统，根文件系统首先在init_main()函数设置了一些信号，即使用run_actions执行某些信号，如重启、关机等。内核一般调用文件系统的时候不传入参数，就会运行parse_inittab()函数来解析inittab。如果永和自己定义了就打开，如果没有配置就执行默认的配置(new_init_action())，这里做的事情就是创建init_action结构体节点，并且把inittab中所有的配置项解析的init_action节点形成一个init_action_list，每一个节点都是inittab的一个配置项，每个配置项都有自己的action和命令脚本。后面做的事情就是执行这些命令(有的执行一次 有的等待 有的一直运行...)，最后根文件系统执行的就是shell一直循环等待用户的命令。
一个最小文件系统都需要什么东西：
- /dev/console
- run_init_process()linuxrc程序(init_main()函数)
- /etc/init.d/rcs--脚本
- shell命令所用到的函数--busybox
- busybox的响应函数运行，需要标准库支持，所以要有glibc
Linux中使用文件系统都分那几个部分
- 有关Linux中高速缓冲区的管理程序 buffer.c,文件系统一般跟高速缓冲区打交道，高速缓冲区再和硬盘。比如分页机制，一页4k。
- 文件系统的底层通用函数(对于硬盘的读写 分配 释放 目录节点管理inode 内存与磁盘的映射)
- 对文件数据进行读写操作的模块(VFS虚拟文件系统 硬件驱动和文件系统的关系 pipe 块设备的读取)
- 文件系统与其他程序的接口实现(fopen close create等)
文件系统的基本概念
磁盘中要有目录的映射，我们把磁盘分成盘片
每一个盘片都有一个文件系统的子系统(章节目录)，由以下几部分组成:
- 引导块:用来引导设备的，可以为空，但要空出来位置
- 超级块:是该文件子系统的描述符(记录盘片的逻辑块位图/i节点位图的地址，通过设备号可以获得)
- i节点位图:每一位对应inode节点的使用情况
- 逻辑块位图:每一位对应一个逻辑块的使用情况
- inode节点:一个结构体，存储文件的索引点、属性、文件名、修改时间、对应的磁盘块(即目录与磁盘的桥接+属性)
- 逻辑块数据区:存储数据的
6.Linux高速缓冲区
高速缓冲区的管理要素
- 映射关系，和磁盘之间的映射关系
- 应用程序与高速缓冲区的交互API，fopen、read、write
- 高速缓冲区与磁盘的交互API(循环链表+哈希表+单链表)
高速缓冲区工作流程
高速缓冲区中存储着对应的块设备驱动的数据，当从块设备中读取数据的时候，OS首先会从高速缓冲区中进行检索，如果没有则从块设备中读出数据，如果有并且是最新的，就直接和该高速缓冲区进行数据交互。
高速缓冲区和磁盘块一一对应
缓冲区可以分为低区和高区，低区(buffer_head结构体)的某一块也对应高区的某一块，类似inode节点位图和i节点。
假如我们来写一个buffer.c
- 分配一个buffer_head,
getblk() - 设置该buffer_head指向空闲缓冲区的一个有效buffer_head,
get_hash_table() - 更新该buffer_head里的所有设置项
- 把该buffer_head从空闲中出链
- 算出该buffer_head对应的散列序号并把它加入到对应的散列项链表尾部
7.inode节点
文件与磁盘的映射结构
每一个盘片都有一个文件系统的子系统(章节目录)，由以下几部分组成:
- 引导块:用来引导设备的，可以为空，但要空出来位置
- 超级块:是该文件子系统的描述符(记录盘片的逻辑块位图/i节点位图的地址，通过设备号可以获得)
- i节点位图:每一位对应inode节点的使用情况，1024 * 8 = 8192个(实际8191，0位不用)
- 逻辑块位图:每一位对应一个逻辑块的使用情况
- inode节点:一个结构体，存储文件的索引点、属性、文件名、修改时间、对应的磁盘块(即目录与磁盘的桥接+属性)
- 逻辑块数据区:存储数据的，是从第一个引导块开始计数的块号
扇区：是一个长度为512B的数据块
在不同的文件系统中，扇区和盘块对应关系是不同的，0.11内核是两个扇区对应一个盘块，最大的文件系统为：1024B * 1024 * 8 = 8M；8M * 8 = 64M，当前linux最大支持64M的块设备大小
不管读取什么磁盘上的资源，都是先getblk(获取该资源对应的设备和块号的高速缓冲区)，然后再bread(确认有效数据的高速缓冲区)，最后进行区域内存的拷贝从从bh(buffer_head)的b_data数据区域拷贝到要用到数据的内存中(buffe(hd read(char * source char * desbuf uint size))
source --> bh->b_data
desbuf --> 硬盘
_bmap(struct m_inode * inode,int block,int create): 对文件进行磁盘映射，也就是给m_inode结构体中的unsigned short i_zone[9] inode节点的磁盘块映射。i_zone前7个存放的是逻辑块号(7K内存)，第八个是一次间接块号(前面是指针，这里就是指针的指针)，指向一个存放512(1个逻辑块号是1k，short类型是2B，所以有512个)个逻辑块号的数组。第九个是二次间接块号(指针的指针的指针)，指向512个一次间接块号。
从磁盘读写数据 信息 inode 等的流程：
- 找到指定的dev
- 通过dev找到设备的super_block
- 通过super_block返回值sb中的信息计算要读的块号
- 调用bread将其读取或写入到高速缓冲区
- 读: 将高速缓冲区的b_data读到你要读的内存地址放高速缓冲区, 写: 将要写入的数据写入高速缓冲区的b_data，并设置dirt修改标志位，等待系统的sys_sync进行写盘,释放高速缓冲区
super.c作用：
- 对设备的超级块进行操作(获取
get_super读取read_supper释放put_supper) - 因为超级块是设备文件系统的映射(代码中的类)，超级块的操作关系到设备的文件系统操作 文件系统的加载/卸载
sys_mountsys_umount - 根文件系统的加载( / )
mount_root
namei.c作用：根据输入字符进行文件目录的建立、删除、打开 节点建立 删除。
namei.c目的：文件系统中的文件操作(打开、权限、属性)、了解文件系统的命令操作(如chmod chown mknod)、c语言中内存区域的检索和管理。
链接文件在内核中就是给已存在的文件，添加一个dir_entry：
- 找到已存在文件的Inode
- 在制定的文件路径中创建一个新的dir_entry
- 把新的dir_entry映射到老的inode上去
8.Linux内存管理
学习目的：
- Linux内存的管理机制(分段 分页)
- 虚拟内存和物理内存的映射方式
- 内存与磁盘的交互(分页机制 缺页重读机制 用时拷贝机制)
- 应用程序如何高效使用内存和高级程序的设计方法
Linux内存使用情况(用户内存和内核内存分开)：
| 内核内存 | 高速缓冲区(包括提供给BIOS的和显存) | [虚拟盘]主内存(用户内存) |
|---|
内存管理名词：
- 逻辑地址：程序员看到的地址，Linux操作系统分配给每一个进程的独立的地址。
- 线性地址：总线地址(=逻辑地址+段基地址)
- 物理地址：物理内存的地址，CPU总线的直接地址
虚拟内存的好处：
- 安全
- 能够提供给进程比物理内存大的多的多的内存空间
- 能够有效管理物理内存，并把零散的内存也映射给完整的虚拟内存
虚拟内存映射到物理内存的方式：
- 分页：包括页目录表(一级页表)和页表(二级页表)，实现从线性地址到物理地址的转换。
- 分段：通过GDT(全局描述符，一个操作系统一张，在setup.S中创建)，每个段有一个段基地址，实现从逻辑地址到线性地址的转换。
GDT从底向上依次为：null->代码段(内核的)->数据段(内核的)->系统段->状态段tss0(任务0)->局部表ldt0(任务0)->状态段tss1(任务1)->局部表ldt1(任务1)->状态段tss2->局部表ldt2......
分段：
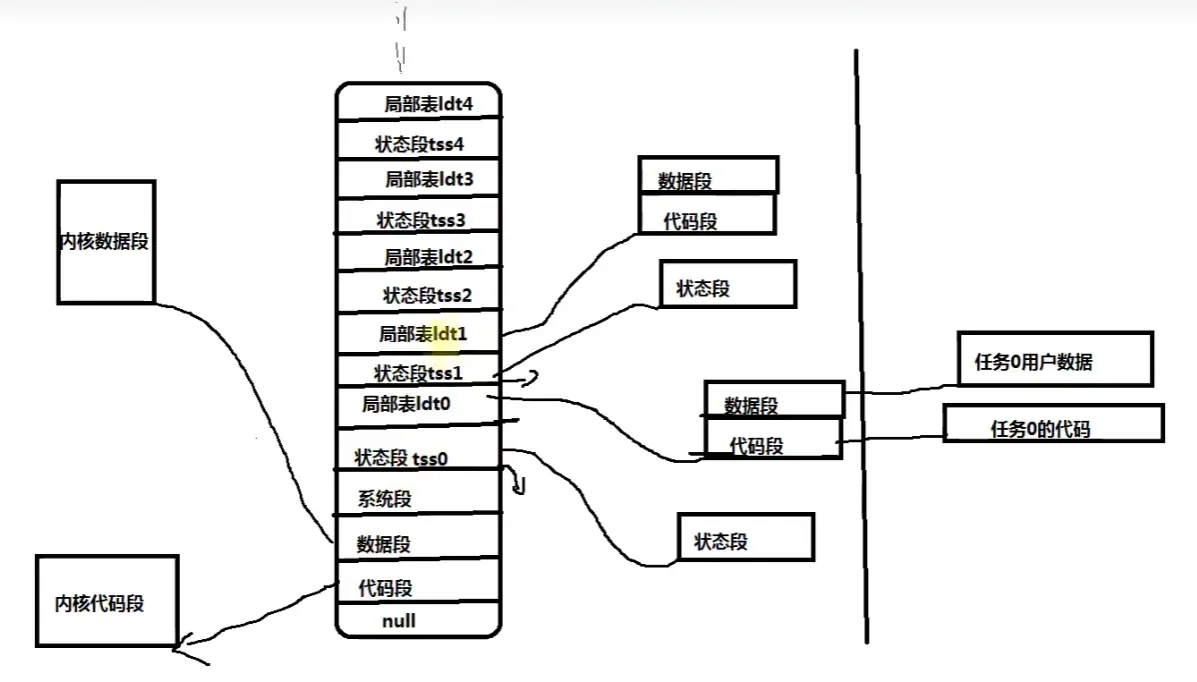
分页：
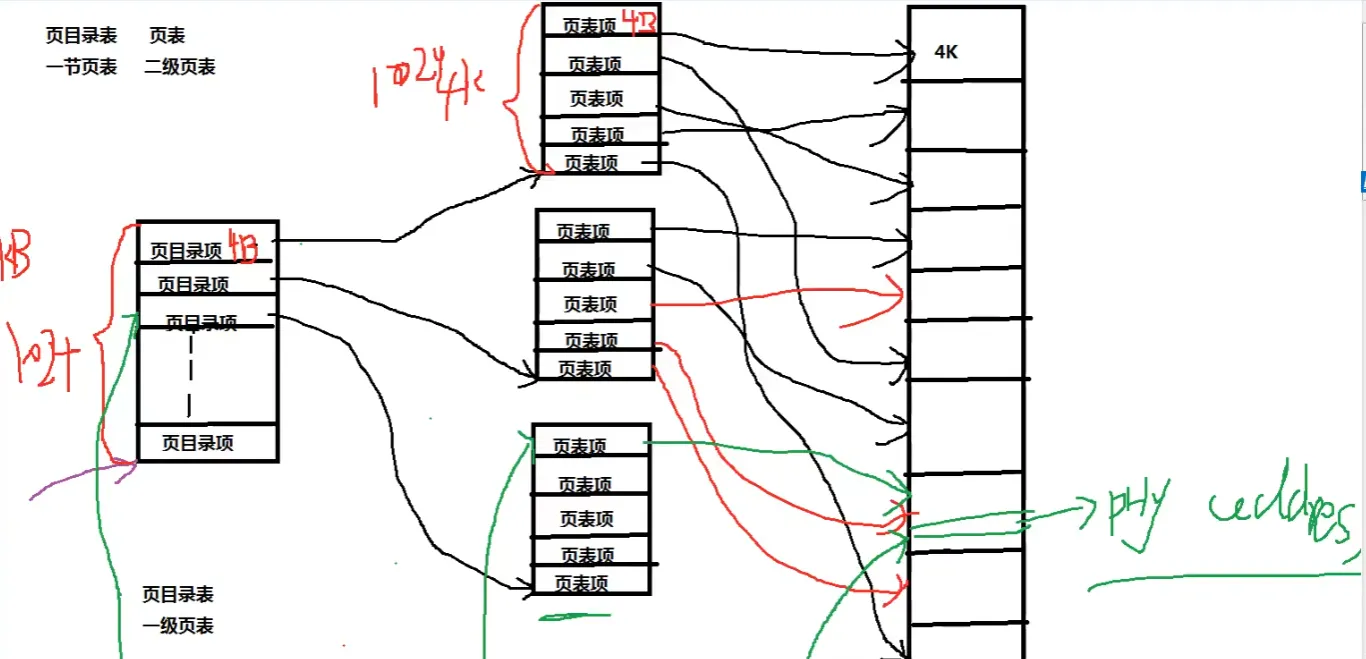
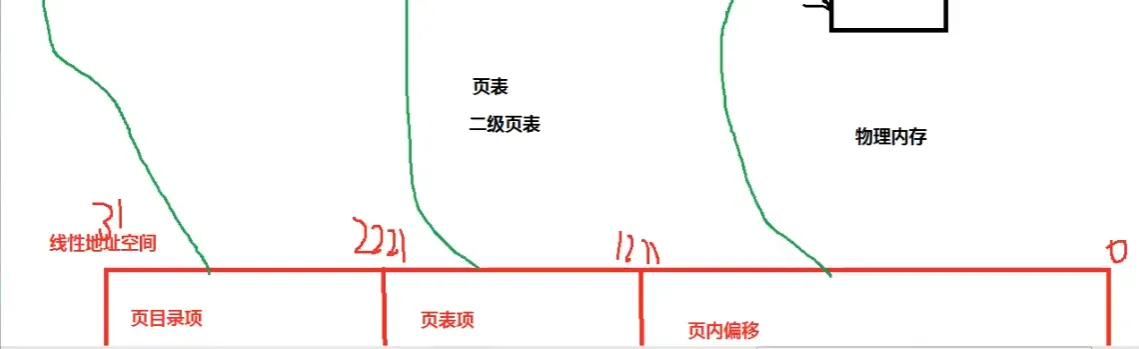
内存管理主要实现了两个重要方式：
-
分页机制：缺页重读，在页目录和页表表项结构中，10位用于页目录寻址，10位用于页表寻址，其余12位的长度供其他权限使用，其中最低位P位是存在位，当P=1的时候该项可用，当目录表项或二级页表表项的P=0时，表示该项无效，通过这种机制实现了我的程序不用全部加载到内存，当用到的时候引发缺页中断再写进内存。倒数第二位R/W表示读还是写，倒数第三位U/S表示用户能用还是super权限能用。倒数第六位是Accessed位表示允不允许访问。倒数第7位表示Dirt位，如果置写了那么会执行同步操作
-
内存读写权限：用时拷贝。在A进程fork() B进程后，只是把A的虚拟内存copy给B，但此时A和B共用一段物理内存，并且把当前的共享内存设置为只读内存。一旦有A或B对这块内存进行写操作时，就会引发页面出错异常
page_fault。在该异常的中断服务函数中，就会首先取消共享内存的操作，并且给写进程复制一个新的物理页面(写多少复制多少)，此时A和B就各自有一块要写的内存，然后设置该内存为可读写状态，然后返回重新进行刚才的写操作。
以上内存分段分页机制是在主内存中，也就是用户内存，在内核内存是不进行分段分页机制的。内核内存结构：
| 向量表 |
|---|
| vmalloc(连续的堆空间) |
| DMA+常规区域映射区(比如kmalloc也是在这里分配，以页为单位，所以内存可能不连续) |
| 高端内存映射区(上面不够了从这里借) |
| 内核模块(xx.ko) |
slab 内存池：适合用在分配大量小对象的情景下(使用buddy算法管理)。创建kmem_cache_create();
ioremap: 物理地址映射为虚拟地址，建立了一个虚拟的页目录 页表等，把指定的物理地址放入建立好的页表关系中。
iounmap: 销毁掉ioremap建立的映射关系。IO读写中专门做寄存器读写的函数：readb readw readl writeb writel，前面函数都是带内存屏蔽的，也就是这行代码等待前面代码执行完再执行(编译乱序情况下)，不带内存屏蔽的是readb_relaxed。
mmap: 做了内存和设备的关联，将用户空间的一段内存与设备关联，当用户访问这段内存的时候就会自动转化为对这段物理内存的访问。
munmap： 取消mmap做的内存和设备的关联。
程序在硬盘到执行做的处理：
- 在运行程序之前，首先从硬盘中把程序的头通过高速缓冲区读到内存(通过fork函数)
- fork-->copy_process(拷贝到栈空间中)-->创建ldt和tss
- 程序运行之前要传入参数和环境变量，创建参数和环境变量的存储页面(在代码段上面)(使用
copy_strings()函数)，设置新函数的sp，重新调整代码段
9.Linux驱动
字符设备驱动
字符设备驱动程序调用过程：用户app->Linux系统调用->虚拟文件系统->具体硬件操作。
写的.c驱动程序添加到sourceinsight中，写.c驱动程序的时候就可以基于内核提供的一些函数，编写代码会有代码补充什么的比较方便。与.c驱动文件在一块的还有个Makefile编译文件，一般结构为：
makefileKERN_DIR = （内核根目录）
all:
make -C $(KERN_DIR) M='pwd' modules
clean:
make -C $(KERN_DIR) M='pwd' modules clean
rm -rf modules.order
#生成char_drv_1.o文件 m表示不加入内核中 如果是y则表示加入内核中
obj-m += char_drv_1.o
Makefile文件在编译时，会通过根目录下的.config文件传入参数，编译的时候会生成auto.conf和autoconf.h文件，auto.conf是给编译用的表示要将那些程序编译到内核镜像中，autoconf.h是给c程序用的， 里面其实添加的宏定义。
写驱动的方法：
- 直接用file_operations写驱动程序，然后register_chrdev注册，参照http://blog.futurezxt.work/post/28 的代码1 2 3。缺点是一个major只能对应一个fops。(2.x版本的内核)
- 3.x版本的内核是每个major对应很多cdev，每个cdev对应minor~minor+size对应一个fops。
- 注册cdev: char_dev_struct;
- 分配cdev：register_chrdev_region(分配第2 3 4个的时候用)和alloc_chrdev_region(分配第一个的时候用)
- cdev_init()对cdev结构体进行清空，设置cdev设备树对象，并和fops绑定。
- cdev_add()把cdev加到所属major的region中
SMP概念：SMP是Symmetric Multi Processing的简称，意为对称多处理系统，内有许多紧耦合多处理器，这种系统的最大特点就是共享所有资源。在这种技术的支持下，一个服务器系统可以同时运行多个处理器，并共享内存和其他的主机资源。一个CPU的多个核可能运行着不同的进程，各种进程之间通信是一个需要解决的复杂问题，有以下几种解决方式：
- 内存屏蔽 barrier
- 中断屏蔽，注册一个中断
request_irq();取消free_irq();定义一个工作队列struct work_struct kindlemem_work();(是把所有的中断下半部放在一个线程中。还有线程中断threaded_irq是把每个中断下半部都作为一个线程)。 - 原子操作：对整形临界区的保护(原理是在操作时对总线进行监控)，相关函数：
atomic_t atomic_a = ATOMIC_INIT(int i)atomic_set(atomic_a, int i)atomic_a = atomic_read(atomic_a)atomic_add()atomic_sub()atomic_inc()atomic_dec()atomic_inc_and_test()atomic_dec_and_test()atomic_sub_and_test()atomic_add_return()set_bit()clear_bit()change_bit()test_bit()test_and_set_bit()。缺点：只能对int做操作。 - 自旋锁spin_lock，定义
spinlock_t lock;初始化spin_lock_init(spinlock_t *lock);锁定/获取锁spin_lock(spinlock_t *lock);释放锁spin_unlock(spinlock_t *lock);锁之间不允许被调度出去，所以要关开中断。 - 自旋锁衍生 读写自旋锁，读写锁优点是可以有多个进程去读，只能有一个进程去写。定义
rwlock_t my_rwlock;初始化rwlock_init(my_rwlock);读锁定read_lock();读解锁read_unlock();写锁定write_lock();写解锁write_unlock();尝试获得write_trylock()。 - 读写自旋锁衍生 顺序自旋锁，优点：多个进程读的时候也能写，判断读完数据有没有变化，如果有变化重读。定义
seqlock_t *my_seqlock;初始化seqlock_init()获得顺序锁write_seqlock()读开始read_seqbegin()重读函数read_seqretry()。 - RCU 读复制更新，专门用于链表操作，保护链表结构体中的结构体对象安全与不发生竞态。读锁定
rcu_read_lock();读解锁rcu_read_unlock();替换list_replace_rcu();更新synchronize_rcu();(阻塞函数) 释放复制的节点kfree();。 - 互斥体，互斥体定义
struct mutex kindle_mutex;初始化mutex_init();获取mutex_lock();释放mutex_unlock();。与锁的区别是允许有进程切换和临界区较大的时候。 - 互斥锁mutex_lock，
- 完成量，一个执行单元执行完之后另外一个才能执行。定义
struct completion kindlemem_completion;也允许上下文切换，等待的任务放在等待队列中。初始化init_completion();等待完成量wait_for_completion()唤醒第一个节点completion();唤醒等待队列所有节点completion_all(); - 信号量，多用于PV操作(生产资源消费资源)同步，定义
struct semaphore kindlemem_semaphore;初始化sema_init()获取down()down_interruptible()释放up()。
DMB: 数据内存屏蔽：保证所有DMB之前的内存访问行为完成。
DSB：数据同步屏蔽：保证DSB之前的所有指令完成操作。
ISB：指令同步屏蔽：刷新CACHE。
子系统驱动
设计思想：同类型的子系统开发一个核心层代码，以输入子系统为例，主要涉及input_dev和input_handler。
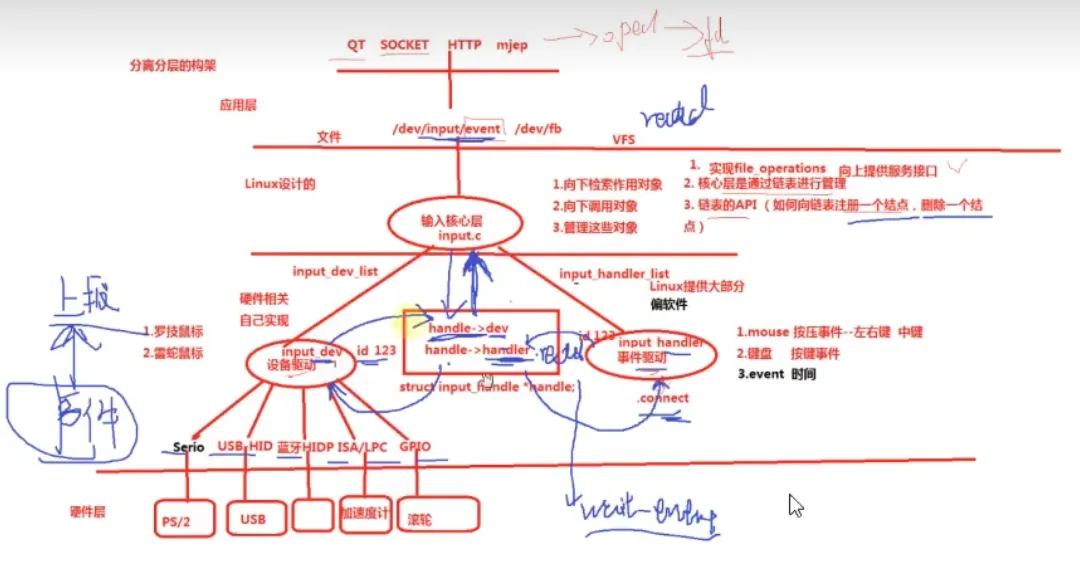
不同鼠标键盘的驱动向核心层注册input_dev和input_handler，最终用户调用read/write一级一级的找到目标硬件设备的驱动。
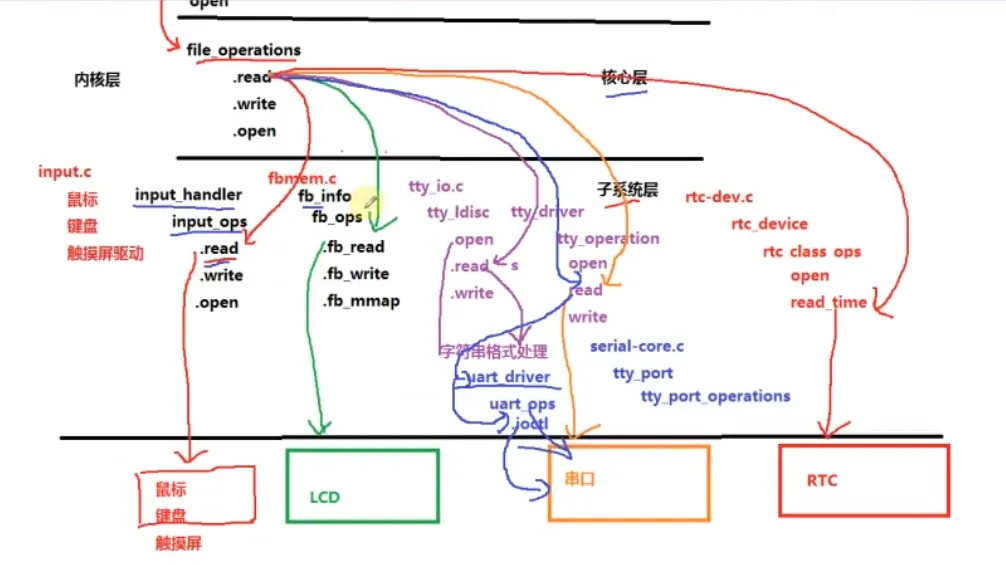
输入子系统驱动
定时器使用方法
- 初始化定时器
init_timer(struct timer_list xx_timer) - 设置定时器的中断函数
xx_timer.function=(void *)xx_timer_handle - 把定时器提交给系统定时器链表
add_timer(&xx_timer) - 触发定时器
mod_timer(&xx_timer,jiffies+HZ/100)
MISC和platform驱动
MISC(多种多样的设备驱动)子系统，是Linux预留的分层结构，在写驱动时如果没有对应的核心层时所使用的，主设备号为10，从设备号可自定义。
对于platform驱动在platform_device中对用到的资源进行描述(IO/中断/mem/DMA)，指定个名字，与platform_driver指定的名字匹配后执行platform_driver的probe函数，进行资源初始化给定fops等。
LCD驱动：核心层fmmem.c
触摸屏驱动：核心层input.c(input_dev和input_handler)，事件驱动。优化：
- 按一个点跳动很大，进行延迟优化，比如按键的去抖动，机械会产生震动。
- 当等待ADC转化的时候，(ADC还没有转化完)但是此时笔已经拍起来了。ADC转化完进行判断，如果此时笔已经抬起来了，丢弃这个点并且转化到等待笔抬起来状态。
- 多次测量取平均，进行精度优化，在ADC的完成中断中 多次触发ADC中断，进行多次测量取平均值。
- 去除在平稳运行中的毛刺点，用数字滤波技术(过滤功能和纠正功能)，比如差分滤波、中值滤波
linux项目-电子相框(Kindle系统构架)
-
硬件设计
- 由客户和系统架构师提出硬件参数需求(CPU 内存 硬盘 外设)
- 硬件原理图工程师设计原理图、Layout工程师设计PCB、硬件选型需要和嵌入式工程师沟通，嵌入式工程师首先和客户沟通，如果客户不懂行凭借自己的经验、公板的demo、评价任务选择。
-
系统构建
- hello world测试看能不能跑(串口能不能用 cpu能不能 能跑几个等，如果有问题找硬件工程师)(bist测试)
- 进行BOOTLOADER的移植，一般用uboot，让uboot提供下载和正常的启动过程。
- 操作系统的移植(选一个合适的Linux内核版本)：系统级别的移植(CPU的适配 内核裁剪(不需要的架构、用不到的驱动等) 分区 兼容性 节能性)。
- 驱动的移植：不仅要考虑硬件，还要考虑操作系统版本(找到芯片的裸板驱动demo，了解相关Linux版本的对应芯片的驱动框架，然后将裸板demo中的硬件操作加入框架中)。
-
底层高级驱动设计
- 设计所有需要使用的硬件驱动，将原芯片demo移植到当前linux内核版本中。主要是熟悉对应芯片的驱动框架，读懂demo怎么控制的硬件。
-
应用层设计
- 应用层库系统构建，如freetype tslib mjpeg socket qt(都是基于根文件系统)
- 库函数编程：通用方法
- 应用程序系统的构架：分层分离设计、顶层设计、模块设计
一、需求确定：
- 显示公司L0G0和显示开机画面
- 读取配置文件，并且按要求加载配置的需求进程
- 人机交互界面的及对话框的设计(前端)
- 电子书的操作
- 菜单 进行书签
- 后台，数据存储方式控制处理 通信
二、设计框架
- 人机交互进程:
- tslib线程:得到触摸上报数据，并上报给事件监听线程
- 按键线程:得到按键上报数据，并上报给事件监听线程
- 事件监听线程:得到底层驱动读写线程的数据后，进行事件的封装
- 事件上报线程:把事件上报给主控线程(添加事件队列的方式)
- 主控线程:把事件队列里面的事件用socket发给后台控制进程
- 后台控制进程:
- SOCKET监听线程:接收其他进程发来的事件
- 主页线程:控制当前LCD显示什么
- 向上线程:准备向上点击后的显示数据，并准备DMA
- 设置线程:
- 存了菜单的图片数据，和多种设置存储线程
- 主控线程:进行事件解析并分发调用其它各种线程
- 网络传输进程
- 文件管理存储进程等等都可以添加
内核信号项目-写一个自己的信号
也是一种中断，所以在system_call.s中会出现。
do_signal不是接受信号然后判断信号值，在中断中执行对应的函数，而是将对应的信号处理程序句柄插入到用户的堆栈中(具体的函数实现代码在文件系统中)。
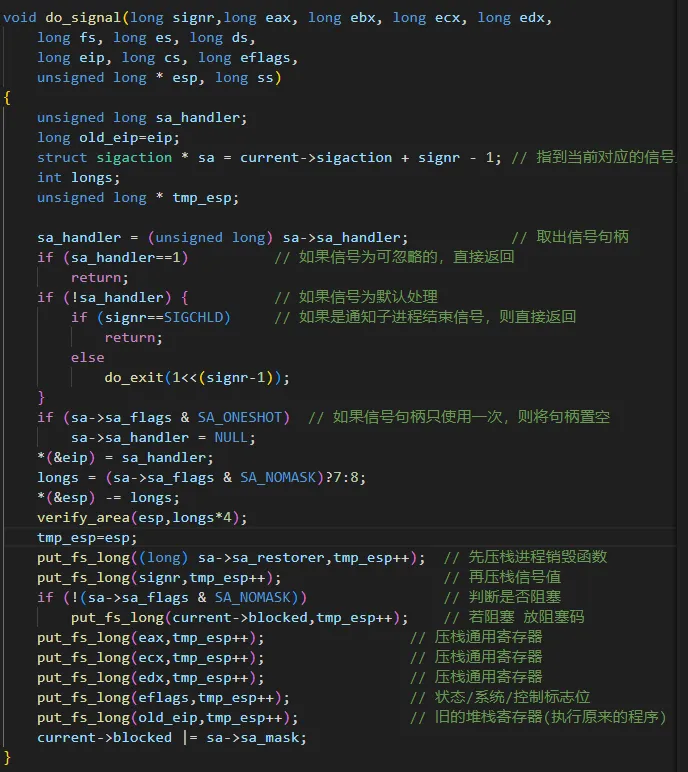
u-boot移植项目
uboot负责设置系统时钟、关闭中断、设置到svc32模式(超级保护模式，复位/软件中断进入)、初始化硬件、进行uboot代码的重定义、给内核进行参数配置(放到tagglist中)、做内核代码的重定义、启动内核。(如果bootloader比较大，做重定位到SDRAM)
在source insight中add代码，尤其arm架构中的只add和单板相关的代码：
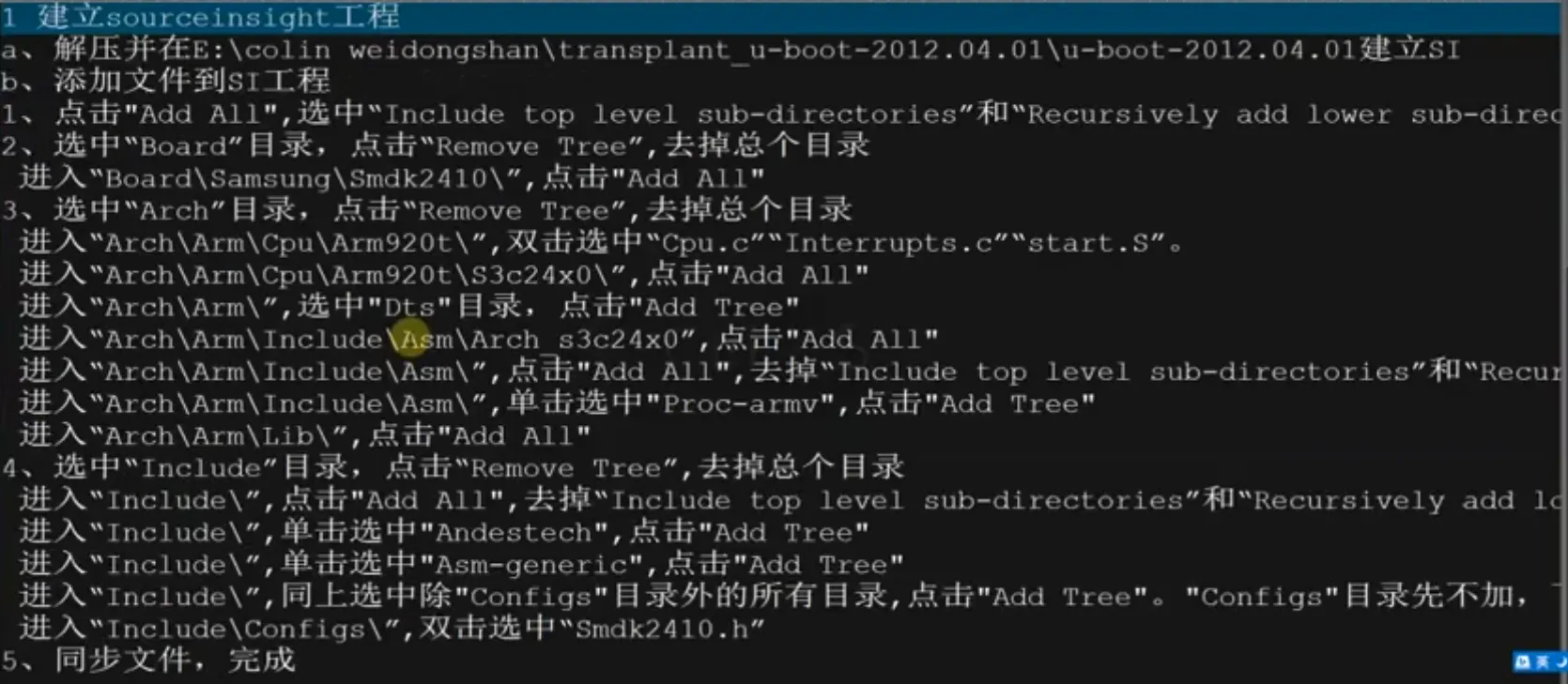
uboot使用过程：
- 根据自己单板的配置文件执行
make xxx_config，会生成config.mk给makefile编译使用，生成config.h给c语言使用。 - 然后编译
make(依赖u-boot.lds文件生成u-boot.bin)
执行的时候程序先执行start.S：
- 定义中断异常向量表
- set the cpu to svc32 mode
- turn off the watchdog
- mask all IROs
- 设置时钟分频系数
- cpu_init_crit()刷新v3/v4cache v4TLB、失能MMU，跳转lowlevel_init()
- 设置了栈
call_board_init_f()运行nand flash的初始化操作 - 把bootloader拷贝到SDRAM上(全部的bootloader)
移植过程：
- 先找一个同型号或者型号相差不大的Demo
- 比如移植smdk2440，先找smdk2410那里出现了
grep "smdk2410" * -nR:
basharch/arm/include/asm/mach-types.h:1645:# define machine_is_smdk2410() (machine_arch_type == MACH_TYPE_SMDK2410)
arch/arm/include/asm/mach-types.h:1647:# define machine_is_smdk2410() (0)
board/samsung/smdk2410/Makefile:8:obj-y := smdk2410.o
boards.cfg:72:Active arm arm920t s3c24x0 samsung - smdk2410 David Müller <d.mueller@elsoft.ch>
有以下文件：mach-types.h:1645、mach-types.h:1647、Makefile:8、boards.cfg:72。
-
boards.cfg是板子配置表(名字、arch、cpu、soc等)，复制粘贴一个目标板卡的，其他文件修改类似。最后配置一下
make smdk2440然后编译make。大概看看错误，下面从头开始修改代码。 -
start.s 修改设置svc32模式(cpsr寄存器定义)，看门狗寄存器位，失能中断，时钟分频，总线模式，启动ICACHE，SDRAM。
虚拟化
通过虚拟化技术可以将一个物理计算机分割为多个虚拟计算机，提高硬件的利用率。
目前全球排名前5的虚拟化软件公司: VMware、微软、红帽(RedHat) 、Oracle等
虚拟机由虚拟化层、虚拟层和管理层三部分组成。
C++智能指针
作用：动态内存管理，动态分配对象之后自动释放资源，防止内存泄漏。
- unique_ptr定义在
<memory>中的一个智能指针，对对象有独有权，两个unique_ptr不能指向一个对象，不能进行复制操作只能进行移动操作。 - shared_ptr是C++标准库中的一个智能指针，共享对一个控制块的访问权限，通过引用计数表示有几个指针指向该对象，计数为0的时候，控制块删除内存资源和自身。
- weak_prt定义在
<memory>中的一个智能指针，协助shared_ptr，解决shared_ptr指针循环引用问题。
unique_ptr和shared_ptr两个智能指针的区别：
- 所有权管理方式：unique_ptr独占式，某一个指针拥有所有权，shared_ptr是共享式，可以好几个指针共同指向某块内存进行控制。
- 内存管理方式不一样：unique_ptr所有权转移方式，shared_ptr使用引用计数的方式。
- 性能：shared_ptr在一个堆上引用计数，构造和赋值比unique_ptr慢，也涉及额外的线程的开销。
Linux客户端与服务端应用
服务器端使用API函数流程:
socket()-->bind()-->listen()-->accept() -->recv ()-->close()
客户端流程使用API函数流程:
socket()-->connect()-->send ()-->close()
select模型：可以同时监听多个文件描述符上的IO事件，从而实现高效地处理并发IO操作。IO多路复用select函数，通过将需要监听的文件描述符以位图的形式传递给select函数，并设置超时时间，当有任何一个文件描述符上的IO事件发生时，select函数返回，开发者可以遍历所有文件描述符来处理就绪事件。可用于网络编程、高并发服务器、IO密集型应用等。
Linux进程管理
ARM64处理器内核地址空间布局
ARM64处理器异常级别
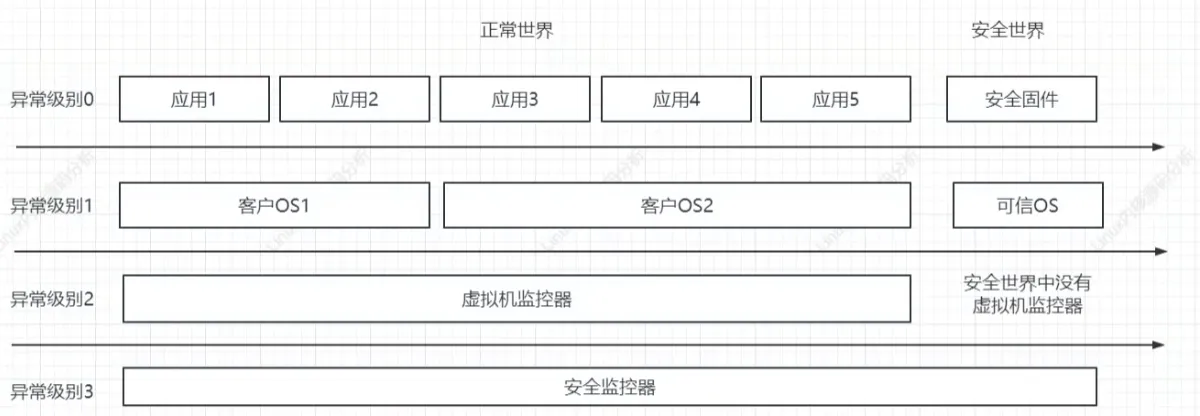
支持虚拟化的异常切换
同步异常：执行指令时生成的异常。
异步异常：中断IRQ、快速中断FIQ、系统错误SE。
异常处理：
- 保存处理器状态到寄存器SPSP_EL1(程序状态寄存器，Saved program status register)
- 保存返回地址在寄存器ELR_EL1(异常链接寄存器)中。
- 把处理器状态的DAIF(debug system irq frq)这4个异常掩码位都设置为1。
- 如果是同步异常或系统错误异常，将异常类别存放到ESR_EL1寄存器中。
- 如果是同步异常，把错误地址保存在寄存器FAR_EL1(错误地址寄存器)。
- 如果处理器处于用户模式(异常级别0)，那么把异常级别提升到1。
- 根据向量基准地址寄存器VBAR_EL1、异常类型和生成异常的异常级别计算出异常向量虚拟地址，执行向量。
CFS调度器
Linux内核作为一个通用操作系统，包括实时进程、交互式进程、批处理进程。
- 交互式进程:与人机交互的进程，比如和鼠标、触摸屏、键盘等相关的应用。vi编辑器、vim编辑器、gedit编辑器。此类进程系统响应时间越块越好，否则用户就会报怨系统卡顿状态。
- 批处理进程:可能会占用比较多的系统资源，例如编译代码等。
- 实时进程:有些应用对整体时延有严格要求，例如现在非常火的VR设备。
操作系统一些命令
shell# 显示file文件的前10行
head -n 10 file
# 显示file文件的后10行
tail -n 10 file
# 合并文件
cat file1 file2 > file3
# 显示大文件时用more，一次显示两行
more -2 file
# 显示当前登录用户的所有信息
who -a
# 显示当前操作系统的信息
uname -a
# 寻求帮助，用于查看命令/函数/文件的帮助信息
man
# 改变文件所有权(chown/chgrp)
chown [] 用户名 文件名称
# 更改文件所有者
chown -R 用户名 文件名
# 更改文件属于的组
chgrp 用户名 文件名
# 修改文件权限
chmod 777 文件名/文件夹
# 创建软链接(快捷方式)
ln 源文件 新文件
# 查看文件的i_node，如果两个文件是软链接关系的话，i_node值一样
ls -li 文件名
# 输入输出重定向(</>)
# '>'将程序的标准输出或标准错误输出重定向到指定的文件或设备
# '<'将标准输入流从键盘改为来自其他文件或其他命令的输出
# ubuntu软件包管理
apt-get
# 查看软件安装位置
dpkg -L 名称
# 或
which 名称
# 查看系统已经安装的包
dpkg --get-selections
# 硬盘发展IDE/SCSI/SATA
# linux文件系统常用的3种类型Ext2/Ext3/Ext4/XFS/JFS
# swap交换分区，类似虚拟内存，当内存不足时，把一部分硬盘虚拟为内存使用
# 挂载文件系统
mount [-t 文件系统类型] [-o 挂载选项，如读写权限访问控制等] 设备文件名 挂载点
# fsck检查及修改文件系统
fsck -C -t 文件系统名
# 在磁盘创建文件系统
mkfs --help
# 建立磁盘分区表
fdisk
# 压缩工具gzip(直接将原文件替换)
gzip 文件名
gzip -r 目录
# 解压
gzip -d 文件名
# 打包压缩工具tar
tar -cvf 生成的文件名.tar file1 file2 目录1 目录2
# 解压
tar -xf 生成的文件名.tar -C 保存的目录
# 其他压缩工具：bzip2/zip
# 显示当前用户执行过的命令历史记录
history
# 管理用户账号，比如修改账号名
usermod -l 新名字 原名字
# 查看用户信息： id命令
id 用户名
# 用户之间切换： su命令
su 用户名
# 监视进程 ps命令，显示当前所有在线用户和运行状态等
ps -aux
# 显示某一个用户的进程
ps -u 用户名
# 即使跟踪进程：top命令
top
# 向进程发送信号 kill向进程发送终止操作
kill PID号
# 调整进程的优先级nice/renice
# 使用ps命令查看进程nice值并降序排列
ps axo pid,comm,nice --sort=-nice
# eth和 ens 区别:一个物理网卡，一个是虚拟网络会话。
# 启动和关闭指定网卡
ifconfig 网卡名 up/down
# 配置IP地址
ifconfig 网卡名 地址
# 报告CPU统计数据： iostat命令，监控系统磁盘IO活动情况，读写速率等。
# I/O监控：iotop命令，内核输出的I/O使用情况，每个进程线程的带宽
# 报告CPU统计数据： mpstat命令
# 虚拟内存统计，使用情况、进程活动、磁盘I/O和CPU使用率
vmstat -a
嵌入式笔记
RTOS
内核态，用户态的区别
区别：运行级别，是否可以操作硬件
用户态->内核态：系统调用、异常、外围设备中断
进程、线程
概述区别
- 地址
- 进程是资源分配的最小单位，线程是CPU调度的最小单位，进程有独立分配的内存空间，线程共享进程空间
- 真正在cpu上运行的是线程
- 开销
- 进程切换开销大，线程轻量级
- 并发性
- 进程并发性差
- 崩溃
-
线程的崩溃不一定导致进程的崩溃
-
线程在进程下行进（单纯的车厢无法运行）
-
一个进程可以包含多个线程（一辆火车可以有多个车厢）
-
不同进程间数据很难共享（一辆火车上的乘客很难换到另外一辆火车，比如站点换乘）
-
同一进程下不同线程间数据很易共享（A车厢换到B车厢很容易）
-
进程要比线程消耗更多的计算机资源（采用多列火车相比多个车厢更耗资源）
-
进程间不会相互影响，一个线程挂掉将导致整个进程挂掉（一列火车不会影响另外一列火车，但如果一列火车上中间的一节车厢着火了，将影响到所有车厢）
-
进程可以拓展到多机，进程最多适合多核（不同火车可以开在多个轨道上，同一火车的车厢不能在行进的不同的轨道上）
-
进程使用的内存地址可以上锁，即一个线程使用某些共享内存时，其他线程必须等它结束，才能使用这一块内存。（比如洗手间）－"互斥锁"
-
进程使用的内存地址可以限定使用量（比如火车上的餐厅，最多只允许多少人进入，如果满了需要在门口等，等有人出来了才能进去）－“信号量”
- 资源占用：每个进程都有独立的内存空间，包括代码、数据、堆栈等，而线程共享所属进程的内存空间。因此，在创建、切换和销毁进程时，涉及到较大的资源开销，而线程切换和创建时的开销较小。
- 并发性：进程是独立运行的执行单位，多个进程之间可以并发，每个进程都有自己的执行状态、程序计数器和堆栈指针等。线程是进程内的执行流，多个线程共享进程的资源，在同一进程中的多个线程可以并发执行。
- 通信和同步：进程间的通信比较复杂，需要通过特定的机制（如管道、消息队列、等）进行数据的传递和共享。而线程之间共享进程的资源，通信相对容易，可以直接访问共享的内存变量。在多线程编程中，线程之间需要通过同步机制（如锁、信号量、条件变量等）来保证数据的一致性和正确性。
- 安全性：由于线程共享进程的资源，多个线程之间对共享数据的访问需要进行同步控制，否则可能会出现竞争条件（Race Condition）和数据不一致的问题。相比之下，进程间的数据相对独立，每个进程拥有独立的内存空间，更加安全。
什么时候使用进程与线程
多进程：
- 优点：进程独立，不影响主程序稳定性，可多CPU运行
- 缺点：逻辑复杂，IPC通信困难，调度开销大
多线程：
- 优点：线程间通信方便，资源开销小，程序逻辑简单
- 缺点：线程间独立互斥困难，线程崩溃影响进程
选择：频繁创建的用线程，CPU密集用进程，IO密集用线程
总结：安全稳定选进程，快速频繁选线程
为什么进程切换比线程切换慢
所需保存的上下文不同
- 进程切换涉及到页表的切换，页表的切换实质上导致TLB的缓存全部失效，这些寄存器里的内容需要全部重写。而线程切换无需经历此步骤。
- 线程切换涉及到线程栈
进程可以创建线程数量
（可用虚拟空间和线程的栈的大小共同决定）一个进程可用虚拟空间是2G，默认情况下，线程的栈的大小是1MB，所以理论上最多只能创建2048个线程
TCB与PCB
线程控制块与进程控制块
PCB：
- 进程ID
- 进程状态寄存器
- 锁、信号量等同步机制与上下文信息
- 进程优先级、等待时间等其他内存
- 内存空间范围
- 线程状态
- 文件描述符
TCB：
- 线程ID
- 线程状态寄存器
- 锁、信号量等同步机制与上下文信息
- 线程优先级
进程上下文切换保存的数据
PCB、CPU通用寄存器、浮点寄存器、用户栈、内核数据结构（页表、进程表、文件表）
线程上下文切换保存的内容
- TCB信息
- 寄存器状态：如R0-R3、SP、LR、PC等
- 程序状态字：如程序处于中断、用户态、内核态等标志位
- 堆栈：线程执行期间所用的变量等信息
- 浮点FPU寄存器
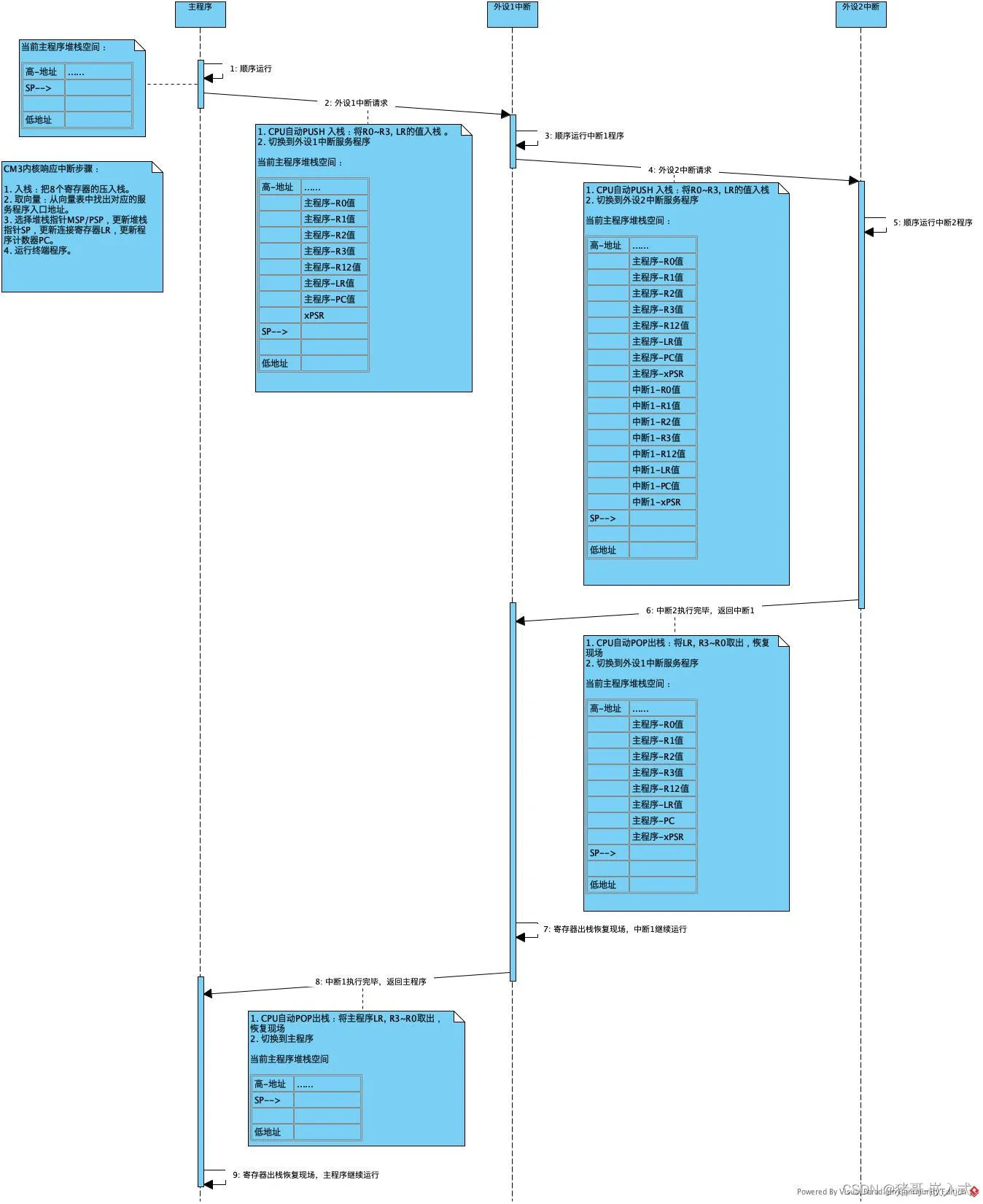
TLB（Translation Lookaside Buffer）
页表的cache，也称为快表，属于MMU的一部分
TLB、页表、Cache、主存之间的访问关系
首先，程序员应该给出一个逻辑地址。通过逻辑地址去查询TLB和页表（一般是同时查询，TLB是页表的子集，所以TLB命中，页表一定命中；但是页表命中，TLB不一定命中），以确定该数据是否在主存中。因为只要TLB和页表命中，该数据就一定被调入主存。如果TLB和页表都不命中，则代表该数据就不在主存，所以必定会导致Cache访问不命中。现在，假设该数据在主存中，那么Cache也不一定会命中，因为Cache里面的数据仅仅是主存的一小部分。
任务调度
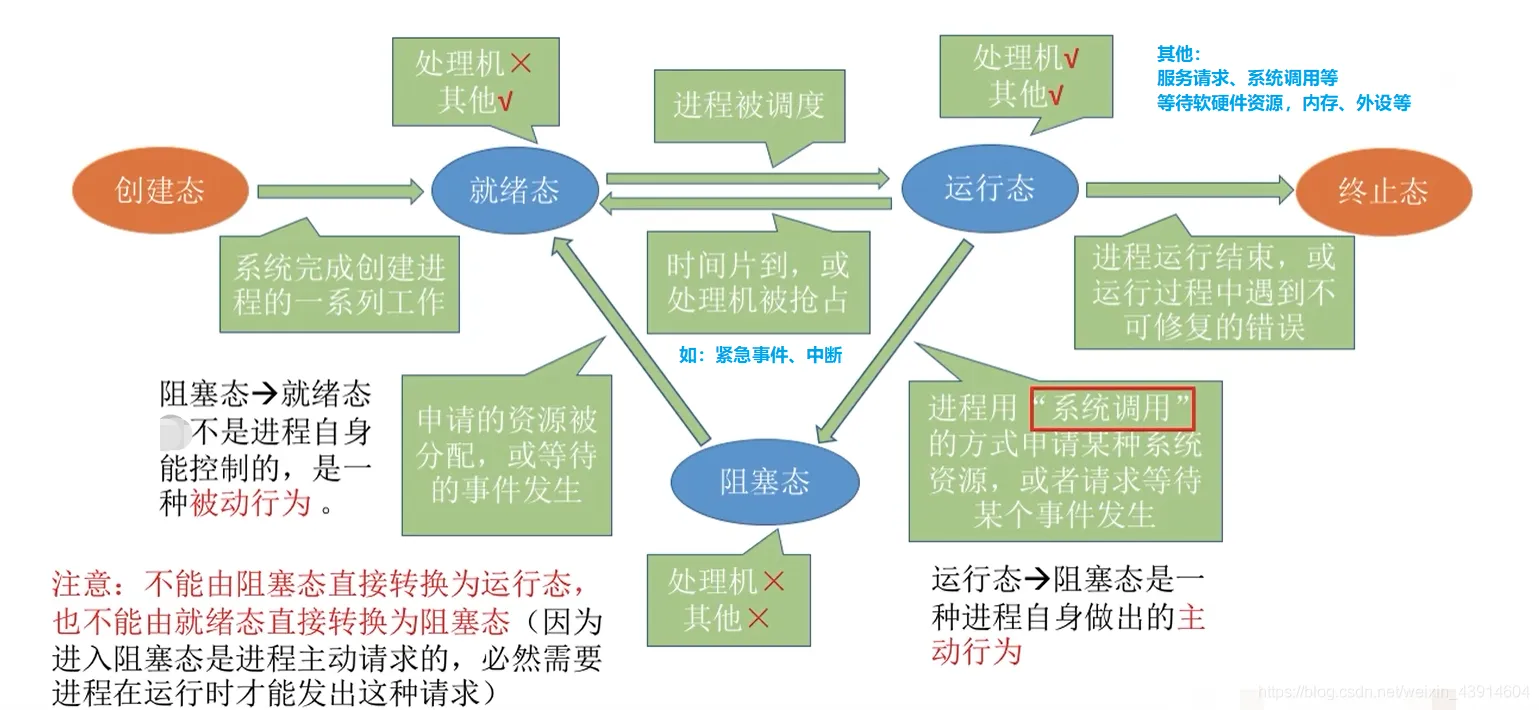
父子进程、僵尸、孤儿
子进程：父进程执行fork()系统调用，复制出一个和自身基本一致的进程为子进程，随后执行exec()系统调用，父进程执行其他任务
孤儿进程： 父进程生成子进程，但是父进程比子进程先结束，系统在子进程结束后回收资源
僵尸进程：子进程已经退出，但是没有父进程回收它的资源
fork()：建立一个新的子进程。其子进程会复制父进程的数据与堆栈空间，并继承已打开的文件代码、工作目录和资源限制等
死锁的原因、条件
两个或两个以上的进程在，因争夺资源而造成的一种互相等待的现象
原因：资源不足、分配不当、推进顺序不合适
条件：
（1） 互斥条件：一个资源每次只能被一个进程使用。 （2） 不剥夺条件：进程已获得的资源，在末释放前，不能强行剥夺。 （3） 请求与保持条件：一个进程因请求资源而阻塞时，对已获得的资源保持不放。 （4） 循环等待条件：若干进程之间形成一种头尾相接的循环等待资源关系。
解除与预防：打破上述一个条件即可
OS中原子操作是如何实现的
底层通过关闭中断或原子指令（硬件支持）的方式
Linux通过原子指令
进程间通信
进程有独立的地址空间，线程公用地址空间。
| 类别 | 信号 | 信号量 | 消息队列 | 管道 | 共享内存 | socket |
|---|---|---|---|---|---|---|
| 描述 | 软中断 | 计数器，同步互斥 | 消息链表 | 无名管道（父子进程间通信）+有名管道（FIFO文件） | 将同一块内存映射到不同进程（最快最有效） | 面向网络的通信 |
| 流向 | 单向 | 单向 | 双向 |
事件不是进程间通信的方式
有名管道、无名管道
进程间通信（IPC）是指操作系统中不同进程之间进行数据交换和共享的机制。无名管道和有名管道都是常见的进程间通信方式。
- 无名管道（Unnamed Pipe）：
- 无名管道是一种半双工的、只能在具有公共祖先的进程之间使用的通信机制。
- 创建无名管道时，操作系统会为其分配一个读端和一个写端。
- 数据通过管道在进程之间单向流动，一端写入数据，另一端从中读取。
- 无名管道通常用于父子进程之间的通信，可以通过fork()系统调用创建。
- 无名管道只能用于有亲缘关系的进程之间的通信，无法被其他进程访问。
- 有名管道（Named Pipe）：
- 有名管道也称为FIFO（First In, First Out），它提供了一种在无亲缘关系的进程之间进行通信的方法。
- 有名管道通过在文件系统中创建一个特殊类型的文件来实现，该文件具有独立的文件名。
- 不同进程可以通过打开该文件并对其进行读写来进行通信。
- 有名管道允许多个进程同时向其中写入数据或者从中读取数据。
- 有名管道可以被许多不相关的进程使用，提供了一种灵活的进程间通信方式。
无名管道和有名管道都是通过读写文件描述符来进行通信的。它们在实现上有所差异，适用于不同的场景和需求。
线程间通信
进程有独立的地址空间，线程公用地址空间。
信号、互斥锁、读写锁、自旋锁、条件变量、信号量
线程间无需特别的手段进行通信，因为线程间可以共享一份全局内存区域，其中包括初始化数据段、未初始化数据段，以及堆内存段等，所以线程之间可以方便、快速地共享信息。只需要将数据复制到共享（全局或堆）变量中即可。不过，要考虑线程的同步和互斥，应用到的技术有：
- 信号 Linux 中使用 pthread_kill() 函数对线程发信号。
- 互斥锁确保同一时间只能有一个线程访问共享资源，当锁被占用时试图对其加锁的线程都进入阻塞状态（释放 CPU 资源使其由运行状态进入等待状态），当锁释放时哪个等待线程能获得该锁取决于内核的调度。
- 读写锁当以写模式加锁而处于写状态时任何试图加锁的线程（不论是读或写）都阻塞，当以读状态模式加锁而处于读状态时“读”线程不阻塞，“写”线程阻塞。读模式共享，写模式互斥。
- 自旋锁上锁受阻时线程不阻塞而是在循环中轮询查看能否获得该锁，没有线程的切换因而没有切换开销，不过对 CPU 的霸占会导致 CPU 资源的浪费。 所以自旋锁适用于并行结构（多个处理器）或者适用于锁被持有时间短而不希望在线程切换产生开销的情况。
- 条件变量 条件变量可以以原子的方式阻塞进程，直到某个特定条件为真为止。对条件的测试是在互斥锁的保护下进行的，条件变量始终与互斥锁一起使用。
- 信号量 信号量实际上是一个非负的整数计数器，用来实现对公共资源的控制。在公共资源增加的时候，信号量就增加；公共资源减少的时候，信号量就减少；只有当信号量的值大于0的时候，才能访问信号量所代表的公共资源。
条件变量condition variable
c++11中，当条件不满足时，相关线程被一直阻塞，直到某种条件出现，这些线程才会被唤醒
- 线程的阻塞是通过成员函数wait()/wait_for()和wait_until()实现
- 线程唤醒是通过函数notify_all()和notify_one()实现
虚假唤醒：在正常情况下，wait类型函数返回时要么是因为被唤醒，要么是因为超时才返回，但是在实际中发现，因此操作系统的原因，wait类型在不满足条件时，它也会返回，这就导致了虚假唤醒。
c++if (不满足xxx条件) {
//没有虚假唤醒，wait函数可以一直等待，直到被唤醒或者超时，没有问题。
//但实际中却存在虚假唤醒，导致假设不成立，wait不会继续等待，跳出if语句，
//提前执行其他代码，流程异常
wait();
}
//其他代码
...
// 实际使用：
while (!(xxx条件) )
{
//虚假唤醒发生，由于while循环，再次检查条件是否满足，
//否则继续等待，解决虚假唤醒
wait();
}
//其他代码
....
案例：生产者消费者模式
c++#include <mutex>
#include <deque>
#include <iostream>
#include <thread>
#include <condition_variable>
class PCModle {
public:
PCModle() : work_(true), max_num(30), next_index(0) {
}
void producer_thread() {
while (work_) {
std::this_thread::sleep_for(std::chrono::milliseconds(500));
//加锁
std::unique_lock<std::mutex> lk(cvMutex);
//当队列未满时，继续添加数据
cv.wait(lk, [this]() { return this->data_deque.size() <= this->max_num; });
next_index++;
data_deque.push_back(next_index);
std::cout << "producer " << next_index << ", queue size: " << data_deque.size() << std::endl;
//唤醒其他线程
cv.notify_all();
//自动释放锁
}
}
void consumer_thread() {
while (work_) {
//加锁
std::unique_lock<std::mutex> lk(cvMutex);
//检测条件是否达成
cv.wait(lk, [this] { return !this->data_deque.empty(); });
//互斥操作，消息数据
int data = data_deque.front();
data_deque.pop_front();
std::cout << "consumer " << data << ", deque size: " << data_deque.size() << std::endl;
//唤醒其他线程
cv.notify_all();
//自动释放锁
}
}
private:
bool work_;
std::mutex cvMutex;
std::condition_variable cv;
//缓存区
std::deque<int> data_deque;
//缓存区最大数目
size_t max_num;
//数据
int next_index;
};
int main() {
PCModle obj;
std::thread ProducerThread = std::thread(&PCModle::producer_thread, &obj);
std::thread ConsumerThread = std::thread(&PCModle::consumer_thread, &obj);
ProducerThread.join();
ConsumerThread.join();
return 0;
}
共享内存
共享内存是进程间通信的一种方式。不同进程之间共享的内存通常为同一段物理内存，进程可以将同一段物理内存连接到他们自己的地址空间中，所有的进程都可以访问共享内存中的地址。如果某个进程向共享内存写入数据，所做的改动将立即影响到可以访问同一段共享内存的任何其他进程。
- 优点：访问高效，通信时无需内核接入避免不必要的复制
- 缺点：没有同步机制，需要手动设计
关闭中断的方式
Cortex-M3和M4中断屏蔽寄存器有三种
- PRIMASK
- FAULTMASK
- BASEPRI
- PRIMASK寄存器设置为1后，关闭所有中断和除了HardFault异常外的所有其他异常，只有NMI、Reset和HardFault可以得到响应。
assemblyCPSIE I; // 清除PRIMASK（使能中断） CPSID I; // 设置PRIMASK（禁止中断）
- FAULTMASK寄存器会把异常的优先级提升到-1，设置为1后关闭所有中断和异常，包括HardFault异常，只有NMI和Reset可以得到响应。
assenblyCPSIE F; // 清除FAULTMASK CPSID F; // 设置FAULTMASK
- BASEPRI寄存器可以屏蔽低于某一个阈值的中断。
设置为n后，屏蔽所有优先级数值大于等于n的中断和异常。Cortex-M的优先级数值越大其优先级越低。
RT-Thread关闭中断
采用汇编代码实现，上述第一种关闭中断的方式，屏蔽全部中断，仅响应HardFault、NMI、Reset
rt_hw_interrupt_disable
assembly;/* ; * rt_base_t rt_hw_interrupt_disable(); ; */ rt_hw_interrupt_disable PROC EXPORT rt_hw_interrupt_disable MRS r0, PRIMASK CPSID I BX LR ENDP
FreeRTOS关闭中断
c#define configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY // 此宏用来设置FreeRTOS系统可管理的最大优先级，也就是BASEPRI寄存器中存放的阈值。
// 关中断
// 向basepri中写入configMAX_SYSCALL_INTERRUPT_PRIORITY,
// 表明优先级低于configMAX_SYSCALL_INTERRUPT_PRIORITY的中断都会被屏蔽
static portFORCE_INLINE void vPortRaiseBASEPRI( void )
{
uint32_t ulNewBASEPRI = configMAX_SYSCALL_INTERRUPT_PRIORITY;
__asm
{
msr basepri, ulNewBASEPRI
dsb
isb
}
}
RT-Thread rt_enter_critical()和rt_hw_interrupt_disable()区别
crt_enter_critical() //禁用调度器，不关闭中断，可嵌套调用，深度65535
rt_hw_interrupt_disable() // 关闭中断，可嵌套调用
FreeRTOS taskENTER_CRITICAL和taskDISABLE_INTERRUPTS区别
cvTaskSuspendAll() // 挂起调度器。不关中断，属于 FreeRTOS 层面，不直接依赖具体的硬件，可嵌套调用
taskENTER_CRITICAL // 支持嵌套调用，底层为关闭部分中断，有引用计数
taskDISABLE_INTERRUPTS // 关闭中断，不支持嵌套，实现方式为配置BASEPRI寄存器，屏蔽某些中断
在下面例子中，调用funcA函数后，再执行完funcB函数后中断就会被打开，从而导致funcC()函数不会被保护。而若使用taskENTER_CRITICAL和taskEXIT_CRITICAL则不会出现这种情况。
c在临界区ENTER/EXIT内流程如下：
ENTER
/* 中断DISABLE */
ENTER
EXIT
/* 此时中断仍然DISABLE */
EXIT
/* 释放所有的临界区,现在才会中断ENABLE*/
但在中断DISABLE内流程则是如下：
DISABLE
/* 现在是中断DISABLE */
DISABLE
ENABLE
/* 即使中断DISABLE了两次，中断现在也会重新使能 */
ENABLE
void funcA()
{
taskDISABLE_INTERRUPT(); //关中断
funcB();//调用函数funcB
funcC();//调用函数funcC
taskENABLE_INTERRUPTS();//开中断
}
void funcB()
{
taskDISABLE_INTERRUPTS();//关中断
执行代码
taskENABLE_INTERRUPTS();//开中断
}
FreeFTOS中断优先级设置
设置FreeRTOS系统可管理的最大优先级，也就是高于5的优先级（小于5的优先级），FreeRTOS不管。
c#define configLIBRARY_LOWEST_INTERRUPT_PRIORITY 15 //中断最低优先级(0-15)
#define configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY 5 //系统可管理的最高中断优先级
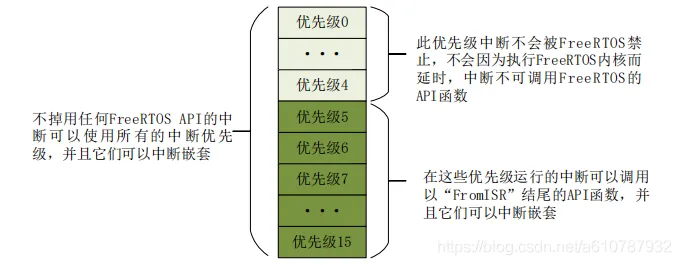
临界区
访问公共资源的程序片段，并不是一种通信方式。
进入临界区的两种方式
ctaskENTER_CRITICAL();
{
.............// 临界区，关闭中断
}
taskEXIT_CRITICAL();
vTaskSuspendAll();
{
.............// 临界区，仅关闭调度器，但响应中断
}
xTaskResumeAll();
互斥锁Mutex、自旋锁Spin
当加锁失败时，互斥锁用「线程切换」来应对，自旋锁则用「忙等待」来应对
互斥锁：Mutex，独占锁，谁上锁谁有权释放，申请上锁失败后阻塞，不能在中断中调用
自旋锁：Spinlock：申请上锁失败后，一直判断是否上锁成功，消耗CPU资源，可在中断中调用
临界区与锁的对比
互斥锁与临界区的作用非常相似，但互斥锁（mutex）是可以命名的，也就是说它可以跨越进程使用。所以创建互斥锁需要的资源更多，所以如果只为了在进程内部使用的话使用临界区会带来速度上的优势并能够减少资源占用量。因为互斥锁是跨进程的互斥锁一旦被创建，就可以通过名字打开它
临界区是一种轻量级的同步机制，与互斥和事件这些内核同步对象相比，临界区是用户态下的对象，即只能在同一进程中实现线程互斥。因无需在用户态和核心态之间切换，所以工作效率比较互斥来说要高很多。
| 使用场景 | 操作权限 | |
|---|---|---|
| 临界区 | 一个进程下不同线程间 | 用户态，轻量级，快 |
| 互斥锁 | 进程间或线程间 | 内核态，切换，慢 |
阻塞与非阻塞区别
阻塞：条件不满足时等待，进入阻塞态直到条件满足被唤醒
非阻塞：条件不满足时立刻返回，继续执行其他任务
RTOS为何不用malloc和free
- 实现复杂，占用空间较多
- 并非线程安全操作
- 每次调用执行时间不确定
- 内存碎片化
- 不同编译器适配复杂
- 难以调试
FreeRTOS内存管理算法
heap_1~5中除了heap_3分配在堆上，其余算法在bss段开辟静态空间进行管理
c// 定义内存堆的大小
#define configTOTAL_HEAP_SIZE (8 * 1024) // 8KB
// 全局变量 "uc_heap" 的定义
static uint8_t ucHeap[configTOTAL_HEAP_SIZE];
uint8_t *ucHeap = ucHeap;
FreeRTOS笔记（六）：五种内存管理详解_CodeDog_wang的博客-CSDN博客
FreeRTOS系列-- heap_4.c内存管理分析_为成功找方法的博客-CSDN博客
| 类别 | 优点 | 缺点 |
|---|---|---|
| heap_1 | 时间确定 | 只分配，不回收 |
| heap_2 | 最佳匹配 | 回收但不合并、时间不确定 |
| heap_3 | 使用标准malloc、free | 代码量大、线程不安全、时间不确定 |
| heap_4 | 最佳匹配、合并相邻 | 时间不确定 |
| heap_5 | 支持多段不连续RAM | 时间不确定 |
- heap_1
- 只分配不回收，不合并空闲区块
- heap_2
- 使用最佳拟合算法分配
- 回收，但不合并，有碎片
- heap_3
- 使用标准库malloc()和free()函数
- heap的大小由链接器配置定义（启动文件定义）
- heap_4
- 使用first fit算法来分配内存
- 合并相邻的空闲内存块
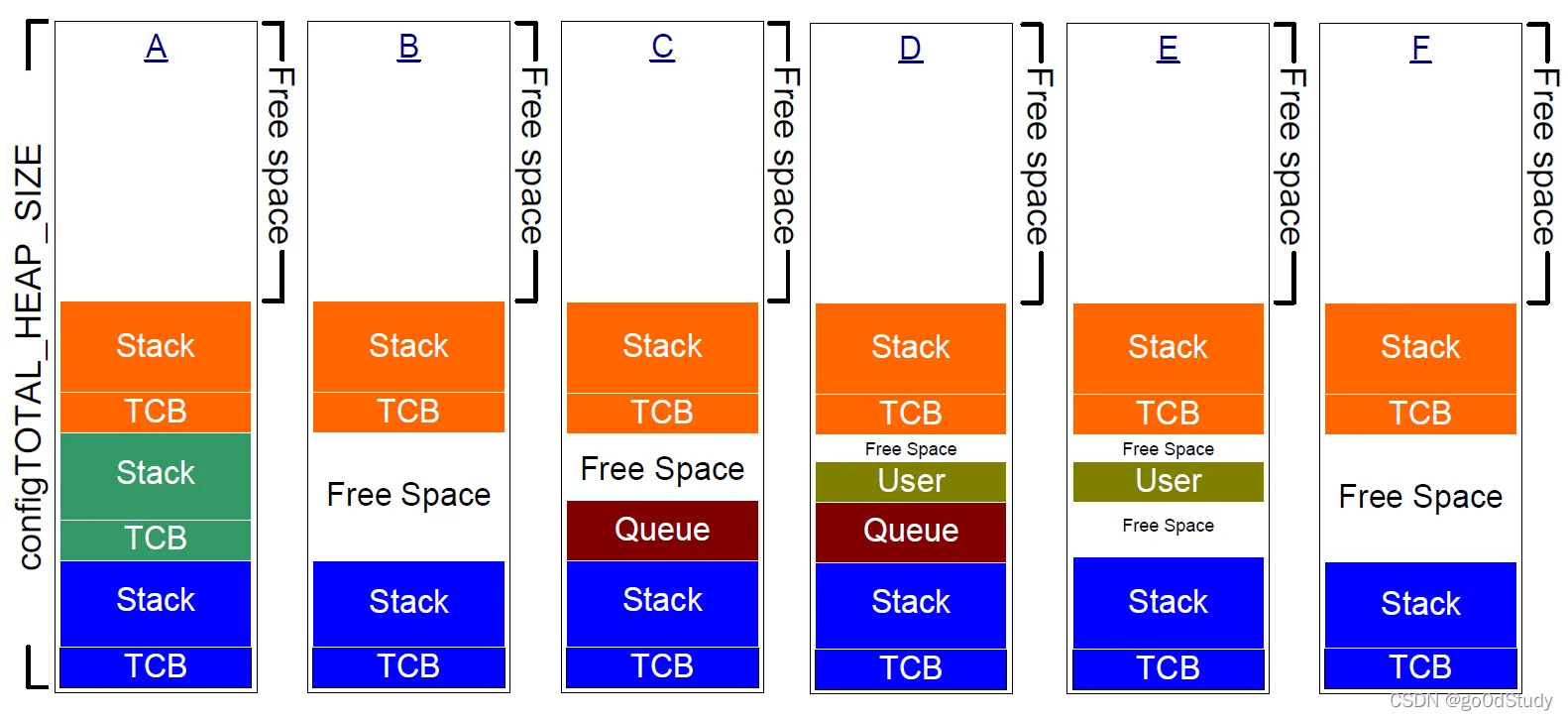
- heap_5
在heap_4的基础上，可以从多个独立的内存空间分配内存
内存池
内存池是一种用于管理和分配内存的技术。它被用于解决频繁地申请和释放内存带来的性能问题。
在传统的内存管理中，当需要使用内存时，通常会通过内存分配函数（如malloc）来动态申请一块内存空间。而释放内存时，则会调用相应的内存释放函数（如free）来释放内存。这种动态的内存分配和释放操作在频繁进行时，会产生很多开销，包括内存管理开销和内存碎片问题。
而内存池就是为了解决这个问题而设计的。它事先申请一定大小的内存空间，并将其划分成多个固定大小的块，形成一个池子。当需要使用内存时，直接从内存池中分配一个可用的块，而不是频繁地调用内存分配函数。在释放内存时，将内存块归还给内存池，而不是调用内存释放函数。
使用内存池的好处是可以降低内存碎片问题，减少动态内存分配和释放的开销。通过一次性申请和释放内存块，可以提高内存分配和释放的效率，从而提升程序性能。此外，内存池还可以提供内存分配的可预测性，避免因动态内存分配造成的不确定性和性能抖动。
RT-Thread内存管理算法
RT-T开辟静态数组的方式管理内存
c#define RT_HEAP_SIZE 6*1024
/* 从内部SRAM申请一块静态内存来作为内存堆使用 */
static uint32_t rt_heap[RT_HEAP_SIZE]; // heap default size: 24K(1024 * 4 * 6)
| 算法 | 文件 | 说明 | 例子 |
|---|---|---|---|
| mem小内存 | mem.c | 2MB以内小内存设备 | 一个瓜--吃多少切多少 |
| slab大内存 | slab.c | 大内存设备，内存池管理 | 一个瓜--已经切好大小--拿对应的 |
| memheap多内存 | memheap.c | 多个内存设备进行合并 | 多个瓜--吃完一个拿下一个 |
- mem小内存管理算法：heap_4
采用链表组织，每个表项包含{magic（是否被非法改写）,used（是否被使用）,next（指针域）,prev（指针域）}
分配64 Bye内存的操作：从表头开始，寻找可用空间进行分配（表头占用3*4 Byte）
释放的操作：更改used表项，查看前后是否为空闲，如有进行合并为大内存块
-
slab大内存管理算法：内存池
为避免频繁分配释放，提前将内存分块
-
memheap内存管理算法：heap_5
将多个不连续的内存地址进行合并拼接
RT-Thread 链表
普通双向循环链表（针对每一个数据结构固定的节点进行操作）
RTT中双向循环链表（数据结构不固定）
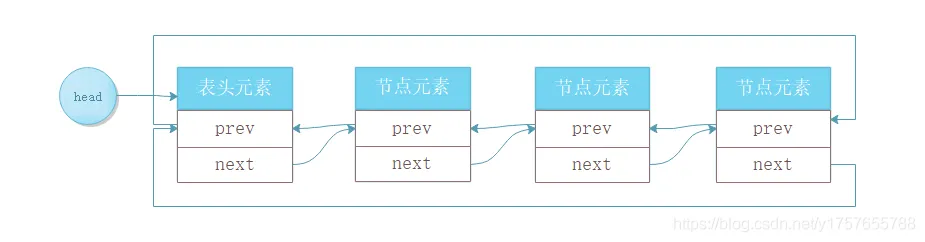
RTT中链表不依赖于节点数据类型，其指针域指向下一个指针域（插入的元素可以为不同类型），
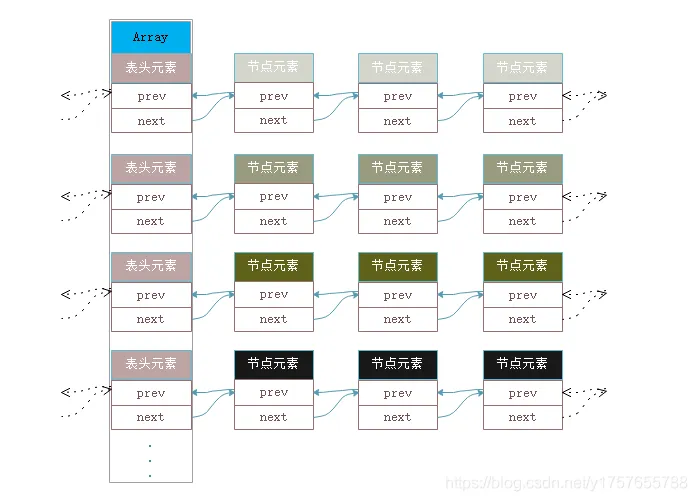
指定节点前插入：
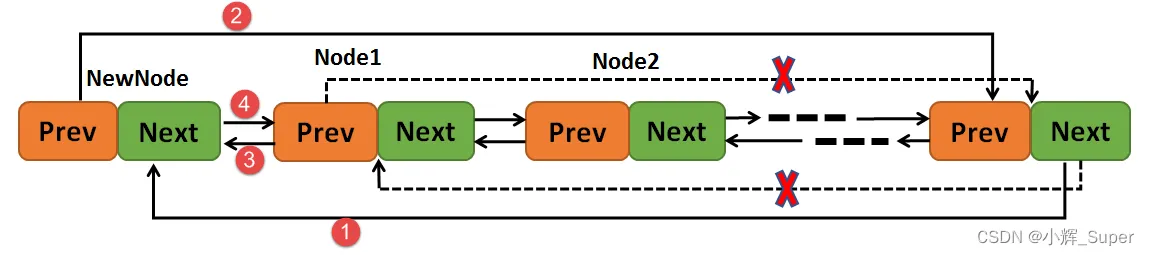
crt_inline void rt_list_insert_before(rt_list_t *l, rt_list_t *n)
{
l->prev->next = n;
n->prev = l->prev;
l->prev = n;
n->next = l;
}
指定节点后插入：
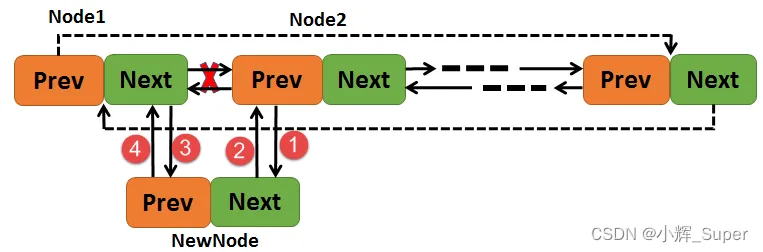
crt_inline void rt_list_insert_after(rt_list_t *l, rt_list_t *n)
{
l->next->prev = n;
n->next = l->next;
l->next = n;
n->prev = l;
}
删除节点：
crt_inline void rt_list_remove(rt_list_t *n)
{
n->next->prev = n->prev;
n->prev->next = n->next;
n->next = n->prev = n;
}
节点元素的访问：
节点中，指针域的存放位置不确定，因此需要一种宏定义，从指针域寻找对应的结构体元素（通过rt_list_t成员的地址访问节点中的其他元素）
既然rt_list_t成员是存放在节点中部或是尾部，且不同类型的节点rt_list_t成员位置还不一样，那在遍历整个链表时，获得的是后继节点（前驱节点）的rt_list_t成员的地址，那如何根据rt_list_t成员的地址访问节点中其他元素。
尽管不同类型节点中rt_list_t成员位置不定，但是在确定类型节点中，rt_list_t成员的偏移是固定的，在获取rt_list_t成员地址的情况下，计算出rt_list_t成员在该节点中的偏移，即(rt_list_t成员地址)-(rt_list_t成员偏移）=节点起始地址。关键在于如何计算不同类型节点中rt_list_t成员偏移。RT-Thread中给出的相应算法如下：
c/**
* Double List structure
*/
struct rt_list_node
{
struct rt_list_node *next; /**< point to next node. */
struct rt_list_node *prev; /**< point to prev node. */
};
typedef struct rt_list_node rt_list_t; /**< Type for lists. */
cstruct rt_thread
{
char name[RT_NAME_MAX]; /**< the name of thread */
rt_list_t list; /**< the object list */
rt_list_t tlist; /**< the thread list */
rt_uint8_t current_priority; /**< current priority */
rt_uint8_t init_priority; /**< initialized priority */
};
typedef struct rt_thread *rt_thread_t;
#define rt_container_of(ptr, type, member) \
((type *)((char *)(ptr) - (unsigned long)(&((type *)0)->member)))
//ptr: 成员首地址（指针域地址，例如 rt_thread_priority_table[highest_ready_priority].next）
//type: 结构体类型（例如 struct rt_thread）
//member: 结构体成员名称（例如 tlist）
RT-Thread 抢占式调度实现
两个线程，低优先级t2任务while(1)执行耗时任务，高优先级t1任务抢占式打印随后阻塞
调度器执行顺序：
1.高优先级任务先执行，执行到rt_thread_mdelay()调用rt_thread_sleep()中的rt_schedule()挂起
2.调度器介入，寻找到当前最高优先级任务（t2）运行
3.低优先级任务时间片未到情况下，由于高优先级任务rt_thread_mdelay()超时，其定时计数器变化
4.下一个节拍周期到达，定时执行rt_tick_increase()，调用rt_timer_check()中的timeout_func()
5.由函数指针跳转到rt_thread_timeout()，执行其中的rt_schedule()
6.进入PendSV中断处理函数进行线程上下文切换
FreeRTOS内存管理
FreeRTOS的内存位于.bss段，并非heap（启动文件中的堆空间大小）
使用pvPortMalloc函数申请内存时，也是从这个系统堆（实际为bss段）中申请的
c#define configTOTAL_HEAP_SIZE ( ( size_t ) ( 100 * 1024 ) // 申请100KB内存用于RTOS系统堆内存
在map文件中可以看到FreeRTOS使用一个静态数组作为HEAP，以我使用的heap_4.c内存管理策略来说，它定义在heap_4.c这个文件里面。因为这个HEAP来自于静态数组，所以它存在于数据段(具体为.bss段)，并不是我一开始认为的FreeRTOS所使用的HEAP来自于系统的堆。
c.bss zero 0x2021'7d1c 0x1'9000 heap_4.o [35] // 实际位于.bss段
Entry Address Size Type Object
----- ------- ---- ---- ------
ucHeap 0x2021'7d1c 0x1'9000 Data Lc heap_4.o [35] // 起始地址与大小
FreeRTOS任务调度
- 系统时钟判断最高优先级任务进行调度
- 当前任务主动执行taskYIELD()或portYIELD_FROM_ISR()让出CPU使用权
FreeRTOS创建任务
在堆中通过pvPortMalloc分配内存给TCB
任务堆栈
在创建任务时，可以选择动态创建或静态创建，静态的任务栈在任务结束后无法被回收，动态的可以
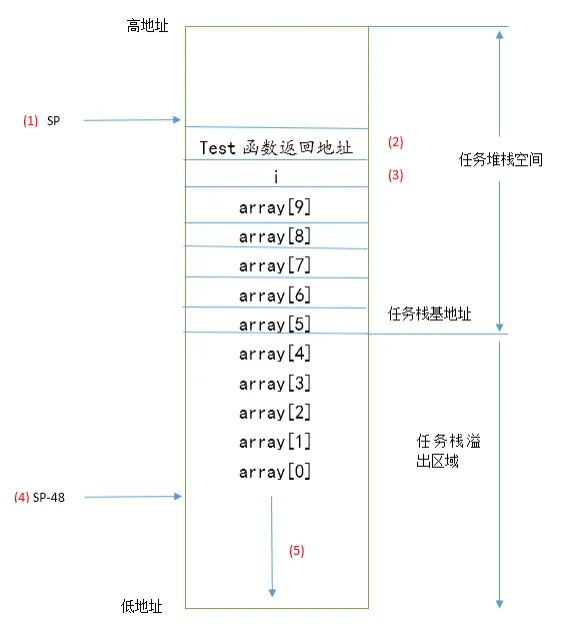
RTOS堆栈溢出的检测
方案1：在调度时检查栈指针是否越界（任务保存有栈顶和栈大小信息，每次切换时检查栈指针是否越界）
- 优点：检测较快
- 缺点：对于任务运行时溢出，而切换前又恢复正常的情况无法检测
方案2：在调度时检查栈末尾的16个字节是否发生改变（创建任务时初始化为特定字符，每次切换时判断是否被改写）
- 优点：可检出几乎所有溢出
- 缺点：检测较慢
RT-Thread PendSV系统调用--上下文切换
省流版：OS调度依赖于systick，最低优先级，ISR抢占OS调度先执行，OS调度在无ISR时实际由PendSV执行，若在调度时ISR到来那么插队执行ISR，再调度
一、方法1-无PendSV-SysTick最高优先级（Fault异常）：
- 假如在产生异常时，CPU正在响应另一个中断ISR，而SysTick的优先级又大于ISR，在这种情况下，SysTick就会抢占ISR，获取CPU使用权，但是在SysTick中不能进行上下文切换，因为这将导致中断ISR被延迟，这在实时要求的系统中是不能容忍的，并且由于IRQ未得到响应，执行了线程，触发Fault异常。
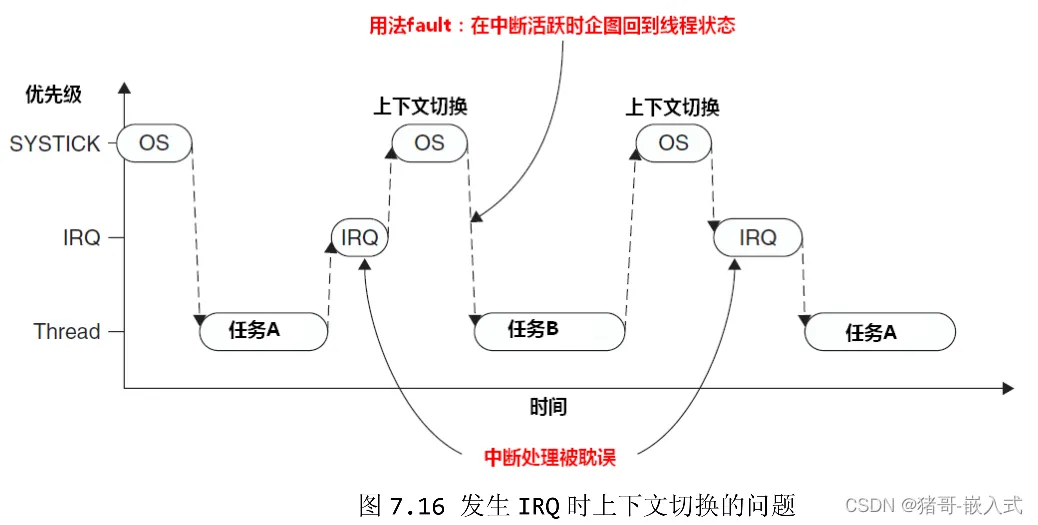二、方法2-无PendSV-SysTick最低优先级（无法满足实时）：
- 将SysTick的优先级设置为最低，然后在SysTick中进行上下文切换
- 一般OS在调度任务时，会关闭中断，也就是进入临界区，而OS任务调度是要耗时的，这就会出现一种情况： 在任务调度期间，如果新的外部IRQ发生，CPU将不能够快速响应处理。
三、PendSV-SysTick最低优先级（实际方案）
- 将SysTick的优先级调低，避免了触发Fault的问题，但是会影响外部中断IRQ的处理速度，那有没有进一步优化的方法呢？答案就是PenSV。因为PendSV有【缓期执行】的特点，所以可以将上图中的OS拆分，分成2段：
- 滴答定时器中断，制作业务调度前的判断工作，不做任务切换。
- 触发PendSV，PendSV并不会立即执行，因为PendSV的优先级最低，如果此时正好有IRQ请求，那么先响应IRQ，最后等到所有优先级高于PendSV的IRQ都执行完毕，再执行PendSV，进行任务调度。（PendSV可被打断）
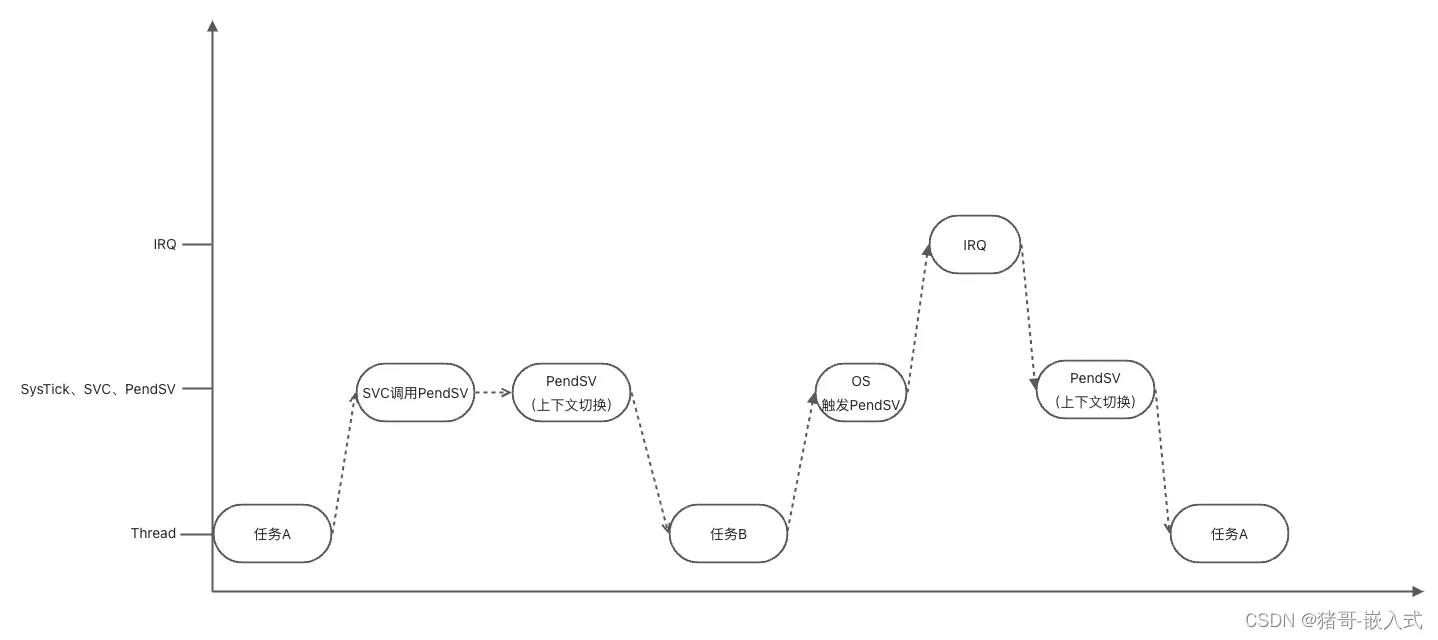
实际方案的缺陷：（系统节拍被ISR打乱）
- SysTick的优先级最低，那如果外部IRQ比较频繁，是不是会导致SysTick经常被挂起，然后滞后，导致Systick的节拍延长，进而导致不准啊？
- 因为1的原因，导致任务的执行调度就不够快了？
四、若将SysTick设置最高优先级，保证系统节拍（实时性不足，无法响应ISR）
- 这样似乎解决了问题，但是又带来了一个问题，SysTick的优先级最高，而且又是周期性的触发，会导致经常抢占外部IRQ，这就会导致外部IRQ响应变慢，
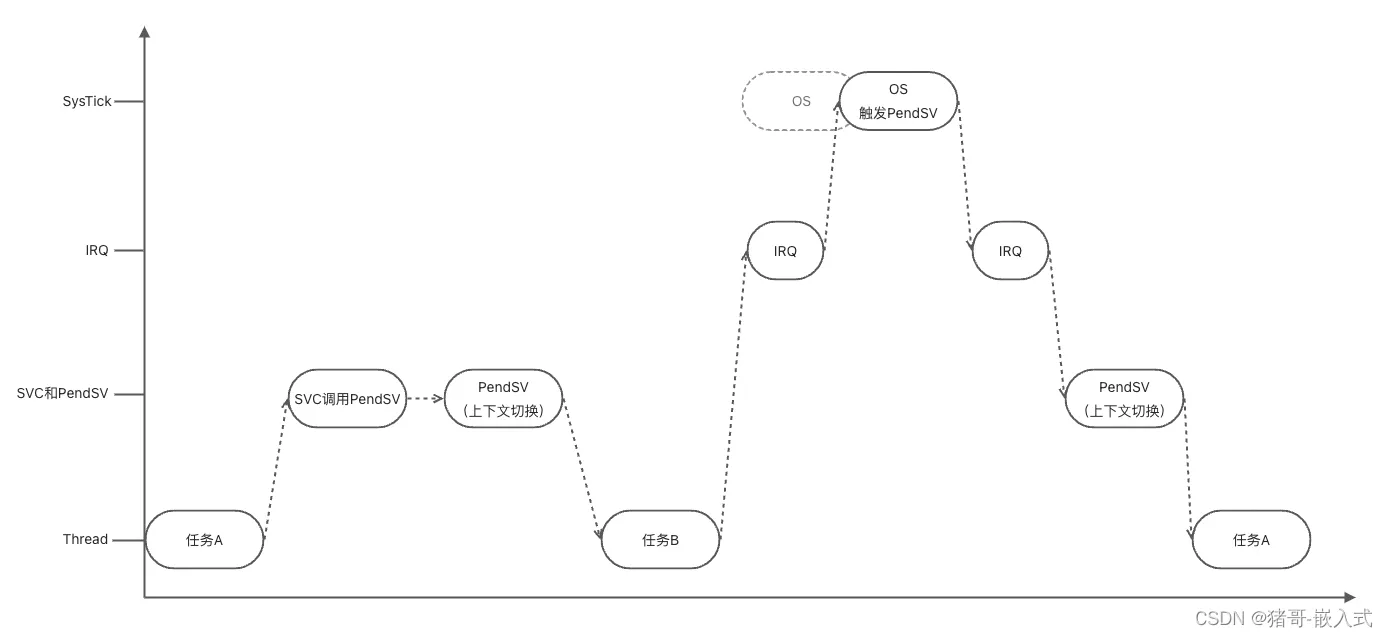
实际方案：
- 滴答定时器中断，制作业务调度前的判断工作，不做任务切换。
- 触发PendSV，PendSV并不会立即执行（优先级最低），如果此时正好有IRQ请求，那么先响应IRQ，最后等到所有优先级高于PendSV的IRQ都执行完毕，再执行PendSV，进行任务调度。
具体实现流程：
1.任务A请求SVC（supervisor call，系统调用）进行任务切换
2.内核收到请求，挂起PendSV异常
3.CPU退出SVC后进入PendSV，执行上下文切换
4.PendSV执行完毕后返回任务B
5.中断发生，执行ISR（子中断服务程序）
6.ISR执行中，心跳到达，SysTick异常发生，抢占了ISR
7.PendSV准备进行上下文切换
8.SysTick退出后，继续执行ISR
9.ISR执行完毕，进入PendSV进行上下文切换
10.切换至任务A
SVC中断
SVC（系统服务调用）和 PendSV（ 可悬挂系统调用 ）。
它们多用于在操作系统之上的软件开发中。 SVC 用于产生系统函数的调用请求。 例如，操作系统不让用户程序直接访问硬件，而是通过提供一些系统服务函数，用户程序使用 SVC 发出对系统服务函数的呼叫请求，以这种方法调用它们来间接访问硬件。因此，当用户程序想要控制特定的硬件时，它就会产生一个 SVC 异常，然后操作系统提供的 SVC 异常服务例程得到执行，它再调用相关的操作系统函数，后者完成用户程序请求的服务。
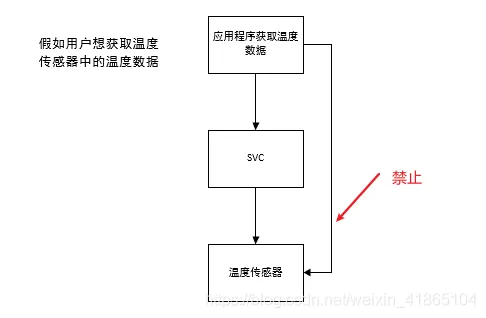系统调用处理异常，用户与内核进行交互，用户想做一些内核相关功能的时候必须通过SVC异常，让内核处于异常模式，才能调用执行内核的源码。触发SVC异常，会立即执行SVC异常代码。
为什么要用SVC启动第一个任务？因为使用了OS，任务都交给内核。总不能像裸机调用普通函数一样启动一个任务。
FreeRTOS中任务调度器触发了 SVC 中断来启动第一个任务，之后的工作都靠 PendSV 和 SysTick 中断触发来实现
SVC是系统服务调用，由 SVC 指令触发调用。在 FreeRTOS 中用来在任务调度中开启第一个任务。触发指令：svc 0
SVC中断就是软中断，给用户提供一个访问硬件的接口PendSV中断相对SVC来说，是可以被延迟执行的，用于任务切换
FreeRTOS中_FROM_ISR
作用：在中断中调用的API，其禁用了调度器，无延时等阻塞操作，保证临界区资源快进快出访问
RT-Thread中没有类似的API，仅有延时参数选项
RT-Thread 同步互斥与通信
| 内核对象 | 生产者 | 消费者 | 数据/状态 | 说明 |
|---|---|---|---|---|
| Semaphore | all | all | 数量0~n | 维护的资源个数 |
| Mutex | A上锁 | 只能A开锁 | bit 0、1 | 单一互斥资源 |
| Event | all | all | 多个bit | 传递事件用以唤醒，实现多任务的同步 |
| Mail box | all | all | 固定4 Byte | 传递指针 |
| Message queue | all | all | 若干数据 | 传递数据（结构体） |
| Signal | 软中断，用以唤醒 |
RT-Thread 消息队列、邮箱、信号量区别
全局变量通信：可以承载通信的内容，但无法告接收方知数据的到达（需要接收方轮询，占用资源）
信号量：告知接收方信息到达，但是未告知数据内容
消息队列：承载了信息内容，同时告知接收方信息到达
邮箱：4 Byte的通信，通过指针而非memcpy()，开销小
RTOS优先级的分配原则
依据任务对响应的敏感性、执行时长（RTOS抢占式，会导致饥饿）
串口接收中断等任务优先级最高
电机PID计算以及控制需要固定控制周期，优先级较高
看门狗，按键处理中等、
最低的APP层的心跳和信息显示任务
FreeRTOS优先级
高优先级数字大
优先级反转
使用信号量时
高优先级任务被低优先级任务阻塞，导致高优先级任务迟迟得不到调度。但其他中等优先级的任务却能抢到CPU资源。-- 从现象上来看，好像是中优先级的任务比高优先级任务具有更高的优先权。
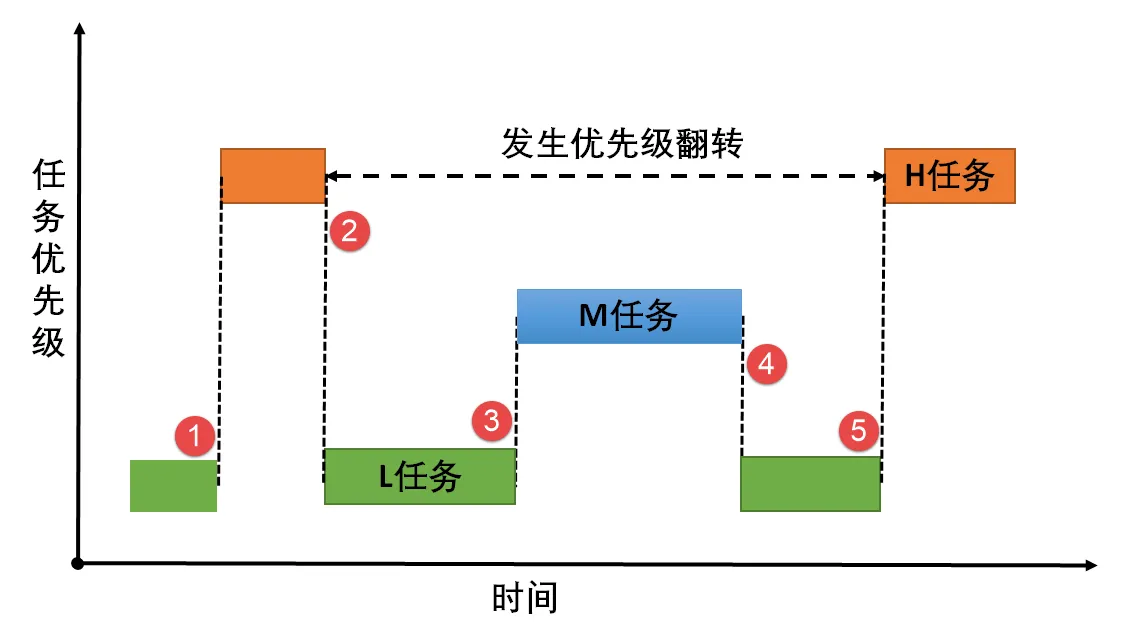
RT-Thread内核移植
CPU架构移植：
在不同的架构，如RISC-V、Cortex-M上运行，上下文切换，时钟配置以及中断操作等的适配
BSP移植：
对于同架构CPU，对不同外设进行适配、动态内存管理
RT-Thread POSIX标准
Portable operating system interface，保证应用程序在不同OS下的可移植性
RT-Thread单元测试
定义：对软件中的最小可测试单元进行检查和验证（函数、方法、类、功能模块）
utest框架（unit test）
RT-Thread 崩溃调试
CmBacktrace 函数，崩溃后保存线程栈和寄存器值，可逆向分析调用关系
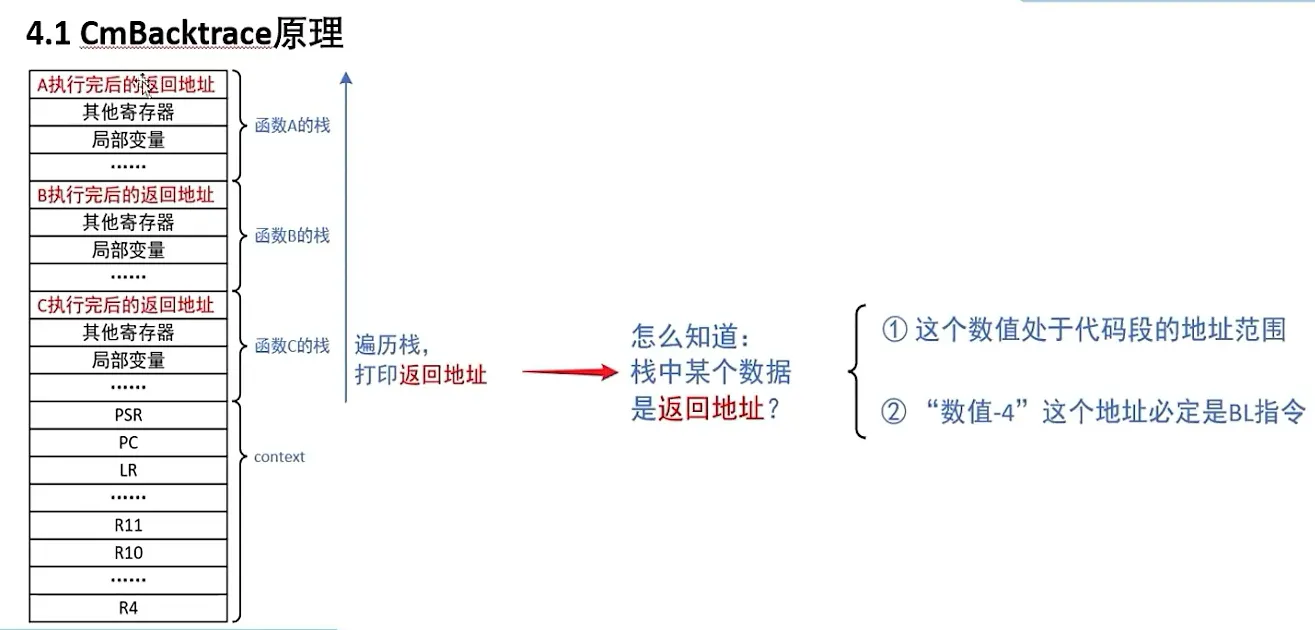
RTOS中多线程看门狗
方案1：在最低优先级线程喂狗，若高优先级线程长时间抢占，则看门狗超时
方案2：监控各线程调度情况，每个线程放置定时任务喂狗，超时则单个线程阻塞
计算机体系结构与硬件
冯诺依曼与哈弗体系结构
冯‘诺依曼体系：计算机硬件由运算器、控制器、存储器、输入设备和输出设备五大部分组成
| 体系 | 冯诺依曼 | 哈佛 | 改进的哈佛（现代ARM） |
|---|---|---|---|
| 数据与程序存储方式 | 存储在一起 | 分开存储 | 分开存储 |
| CPU总线条数 | 1*(地址+数据) | 2*(地址+数据) | 1*(地址+数据)（新增cache，cpu由1条总线读cache，cache有2条总线） |
| 取指操作与取数据操作 | 串行 | 并行，可预取指 | 并行，可预取指 |
| 缺点 | 成本低 | 成本高 | 综合 |
| 优点 | 执行效率低 | 效率高，流水线（取指、译码、执行） | 同哈佛 |
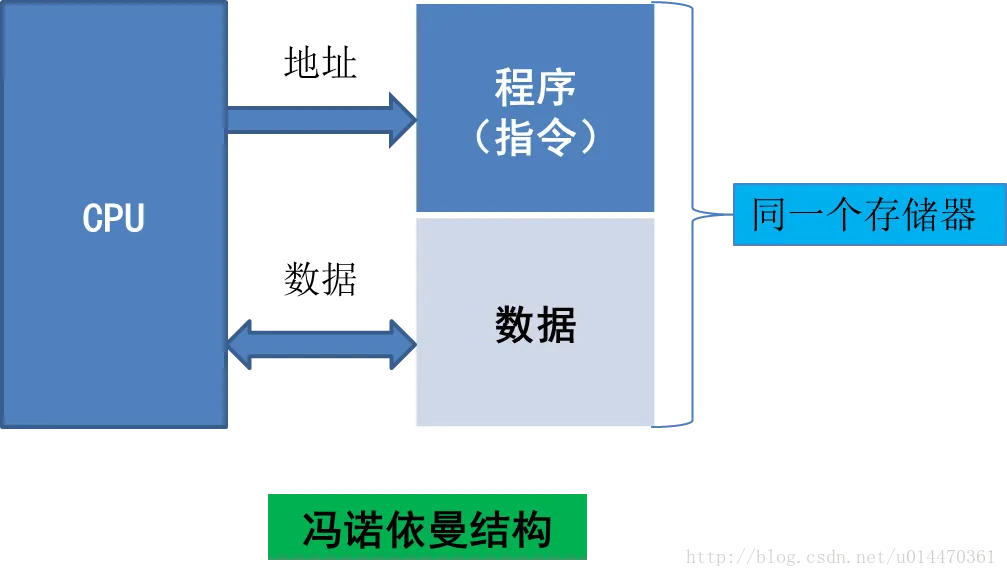
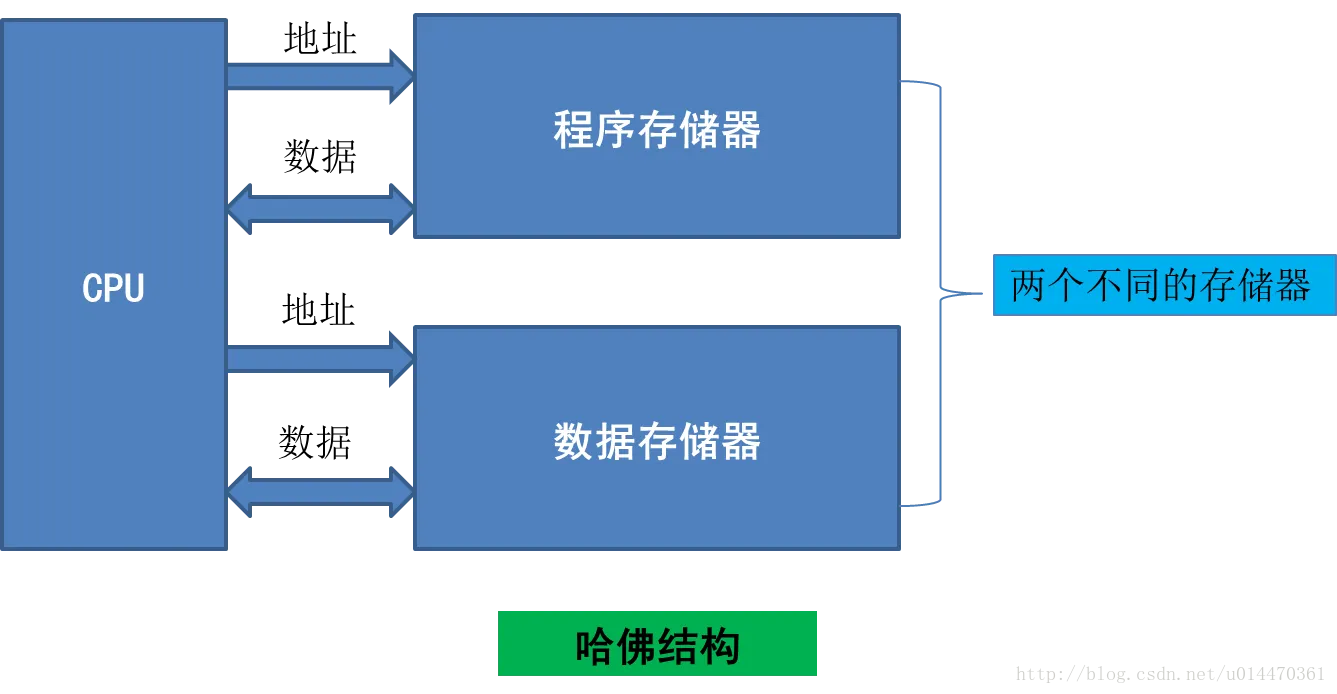
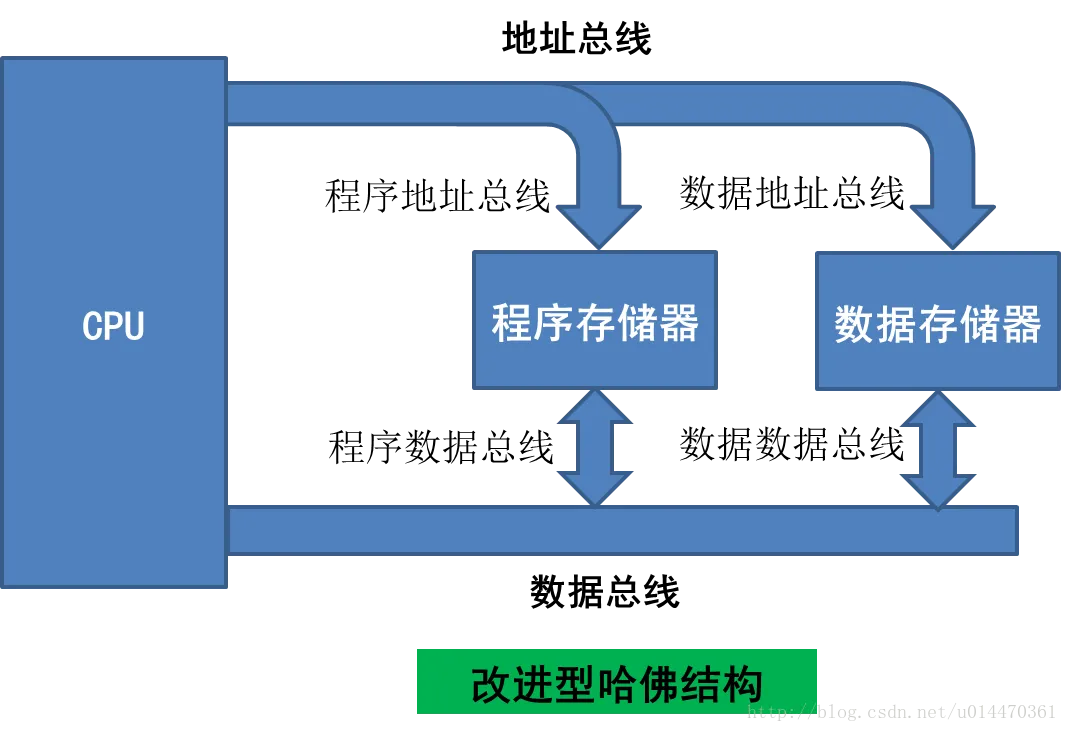
ARM架构与x86架构区别
最主要区别：指令集
- ARM：精简指令集RISC
- X86：复杂指令集CISC
功耗
- ARM：主要面向低功耗
- X86：通过制程弥补功耗劣势
性能
ARM：低性能，顺序执行能力强，流水线指令集，主频低于1G
X86：高性能，乱序执行能力强，主频高
流水线
CPU的流水线（Pipeline）是一种提高处理器执行效率的技术，将指令执行过程划分为多个阶段，并使多个指令在不同阶段之间并行执行，从而实现指令级并行。
CPU流水线通常包括以下几个阶段：
- 取指（Instruction Fetch）：从内存中获取下一条指令。
- 译码（Instruction Decode）：将指令解析成对应的操作码和操作数，并为执行阶段做准备。
- 执行（Execute）：执行指令的具体操作，如算术运算、逻辑运算等。
- 访存（Memory Access）：如果指令需要访问内存，这个阶段用于进行数据的读取或写入操作。
- 写回（Write Back）：将执行结果写回到寄存器中，更新寄存器的内容。
每条指令在流水线中按顺序通过不同的阶段，形成一个连续的流水线操作。当一个指令完成当前阶段的操作后，就会进入下一阶段，同时下一条指令进入到当前阶段，从而实现指令的并行执行。
通过流水线技术，CPU可以实现更高的处理能力和更好的性能指标，因为在同一时钟周期内可以同时执行多个指令。然而，流水线也会引入一些问题，如流水线的阻塞、冲突和分支预测问题，可能导致流水线效率下降。为了解决这些问题，还可以采取一些技术手段，如超标量流水线、动态调度、乱序执行等。
一个任务执行阶段，开始下一个任务的取指、译码阶段
- 提高了吞吐量，但单任务的执行时间没有减少
- 受制于最慢的流水线
- 对程序员不可见
RISC5级流水线步骤
- 取指（访问Icache得到PC）
- 译码（翻译指令并从寄存器取数）
- 执行（运算）
- 访存（访问存储器，读取操作数）（4级流水线独有）
- 写回（将结果写回寄存器）（5级流水线独有）
ARM3级流水线步骤
- 取指
- 译码
- 执行
CPU、MCU、SOC区别
- CPU：运算器、控制器、寄存器组成，主要负责取指、放入寄存器、译码、执行指令并更新寄存器（仅存在理论之中）
- MPU：增强版的CPU
- MCU：CPU+RAM+ROM+I/O，在CPU的基础上加入片上RAM、Flash、串口、ADC等外设，在一块芯片上集成整个计算机系统
- SOC：MPU+RAM+ROM+I/O+特定功能模块（如电能计量、编解码），将MPU的计算能力和MCU的外设结合
Cache
高速 中等速度 低速
CPU <------> Cache <-----> RAM
Cache，就是一种缓存机制，它位于CPU和DDR RAM之间，为CPU和DDR之间的读写提供一段内存缓冲区。cache一般是SRAM，它采用了和制作CPU相同的半导体工艺，它的价格比DDR要高，但读写速度要比DDR快不少。例如CPU要执行DDR里的指令，可以一次性的读一块区域的指令到cache里，下次就可以直接从cache里获取指令，而不用反复的去访问速度较慢的DDR。又例如，CPU要写一块数据到DDR里，它可以将数据快速地写到cache里，然后手动执行一条刷新cache的指令就可以将这片数据都更新到DDR里，或者干脆就不刷新，待cache到合适的时候，自己再将内容flush到DDR里。总之一句话，cache的存在意义就是拉近CPU和DDR直接的性能差异，提高整个系统性能。
Cache分为I-Cache（指令缓存）与D-Cache（数据缓存）
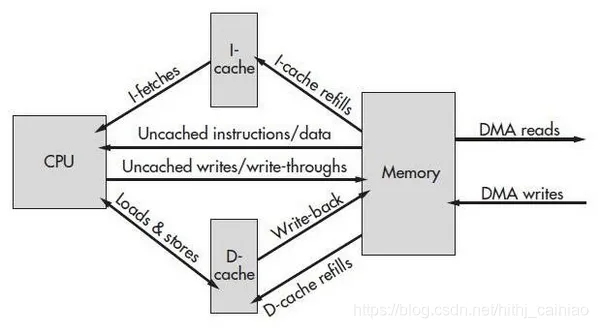
cache是多级的，在一个系统中你可能会看到L1、L2、L3, 当然越靠近core就越小，也是越昂贵。
CPU接收到指令后，它会最先向CPU中的一级缓存（L1 Cache）去寻找相关的数据，然一级缓存是与CPU同频运行的，但是由于容量较小，所以不可能每次都命中。这时CPU会继续向下一级的二级缓存（L2 Cache）寻找，同样的道理，当所需要的数据在二级缓存中也没有的话，会继续转向L3 Cache、内存(主存)和硬盘.
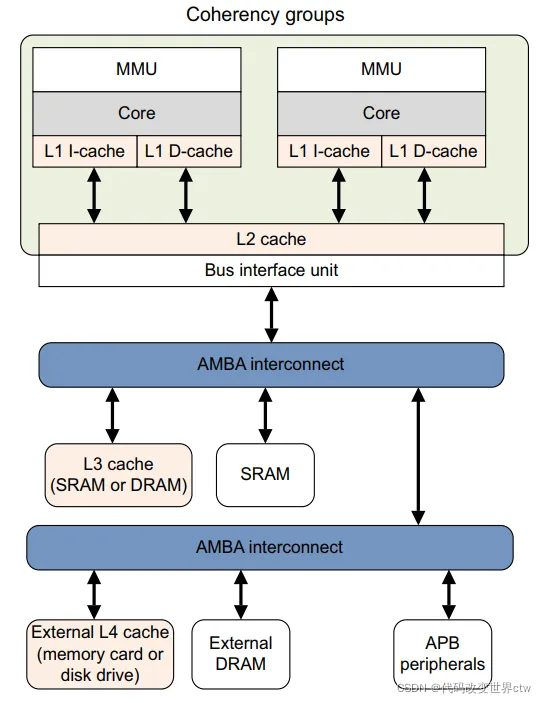
不能使用cache的情况
- CPU读取外设的内存数据，如果外设的数据本身会变，如网卡接收到外部数据，那么CPU如果连续2次读外设的操作相差时间很短，而且访问的是同样的地址，上次的内存数据还存在于cache当中，那么CPU第二次读取的可能还是第一次缓存在cache里数据。
- CPU往外设写数据，如向串口控制器的内存空间写数据，如果CPU第1次写的数据还存在于cache当中，第2次又往同样的地址写数据，CPU可能就只更新了一下cache，由cache输出到串口的只有第2次的内容，第1次写的数据就丢失了。
- 在嵌入式开发环境中，经常需要在PC端使用调试工具来通过直接查看内存的方式以确定某些事件的发生，如果定义一个全局变量来记录中断计数或者task循环次数等，这个变量如果定义为cache的，你会发现有时候系统明明是正常运行的，但是这个全局变量很长时间都不动一下。其实它的累加效果在cache里，因为没有人引用该变量，而长时间不会flush到DDR里
- 考虑双cpu的运行环境(不是双核)。cpu1和cpu2共享一块ddr，它们都能访问,这块共享内存用于处理器之间的通信。cpu1在写完数据到后立刻给cpu2一个中断信号，通知cpu2去读这块内存，如果用cache的方法，cpu1可能把更新的内容只写到cache里，还没有被换出到ddr里，cpu2就已经跑去读，那么读到的并不是期望的数据。
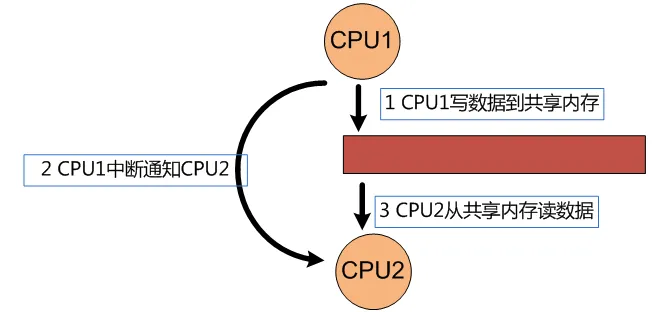
为何启动时关闭Cache
在嵌入式系统和某些应用程序中，启动时关闭指令缓存（Instruction Cache）和数据缓存（Data Cache）是一种常见的做法。以下是一些原因：
- 避免缓存冲突：在启动阶段，代码和数据通常是从外部存储器（如闪存）加载到内部存储器（如RAM）中。由于这些加载过程往往涉及重复的读写操作，启动时关闭缓存可以防止缓存中的“旧”数据对加载过程产生冲突，确保正确加载并执行新的代码和数据。
- 简化启动过程：在关闭缓存的情况下，处理器将直接从内存中读取指令和数据，而不依赖于缓存。这样可以避免额外的缓存管理开销，并简化启动代码的编写和调试过程。
- 确保数据的一致性：某些应用程序要求数据在内存和外部设备之间保持一致。在关闭缓存的情况下，每次访问数据都将直接从内存取，确内存中的数据始终与外部设备保持一致，关闭存并不适用于所有应用场景，并且可能会对性能产生负面影响。在实际应用中，应根据具体的系统需求和性能要求来决定是否关闭缓存。
存储器层次结构与分类
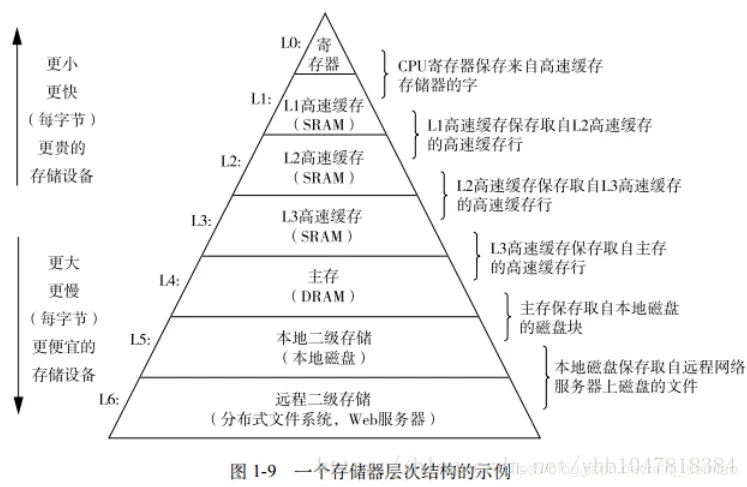
Cortex-M
寄存器
Cortex-M 系列 CPU 的寄存器组里有 R0~R15 共 16 个通用寄存器组和若干特殊功能寄存器
SP指向：栈顶
LR指向：函数调用结束后的返回地址
PC指向：下一条指令
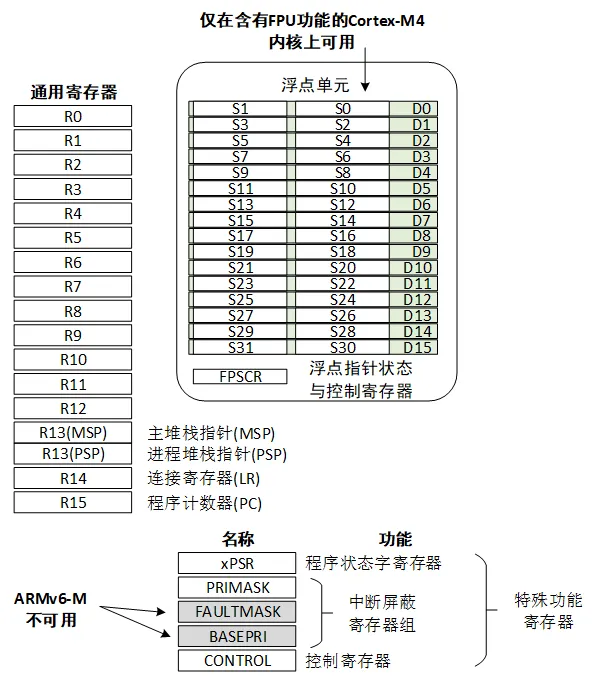
寄存器R13在ARM指令中常用作堆栈指针SP，寄存器R14称为子程序链接寄存器LR(LinkRegister)，寄存器R15用作程序计数器(PC)。 ARM微处理器共有37个32位寄存器，其中31个为通用寄存器，6个位状态寄存器。通用寄存器R0~R14、程序计数器PC（即R15）是需要熟悉其功能的。
R13 SP MSP PSP
MSP的含义是Main_Stack_Pointer，即主栈 PSP的含义是 Process_Stack_Pointer,即任务栈
- Cortex-M3内核中有两个堆栈指针（MSP & PSP），但任何时刻只能使用到其中一个。
- 复位后处于线程模式特权级，默认使用MSP。
- 通过SP访问到的是正在使用的那个指针，可以通过MSR/MRS指令访问指定的堆栈指针。
- 通过设置CONTROL寄存器的bit[1]选择使用哪个堆栈指针。CONTROL[1]=0选择主堆栈指针；CONTROL[1]=1选择进程堆栈指针。
- Handler模式下，只允许使用主堆栈指针MSP。
典型的OS环境中，MSP和PSP的用法如下：
- MSP用于OS内核和异常处理。
- PSP用于应用任务。
- CONTROL的bit1为0，SP = MSP CONTROL的bit1为1，SP = PSP
在裸机开发中，CONTROL的bit1始终是0，也就是说裸机开发中全程使用程MSP，并没有使用PSP。在执行后台程序(大循环程序)SP使用的是MSP，在执行前台程序(中断服务程序)SP使用的是MSP。 在OS开发中，当运行中断服务程序的时候CONTROL的bit1是0，SP使用的是MSP；当运行线程程序的时候CONTROL的bit1是1，SP使用的是PSP。
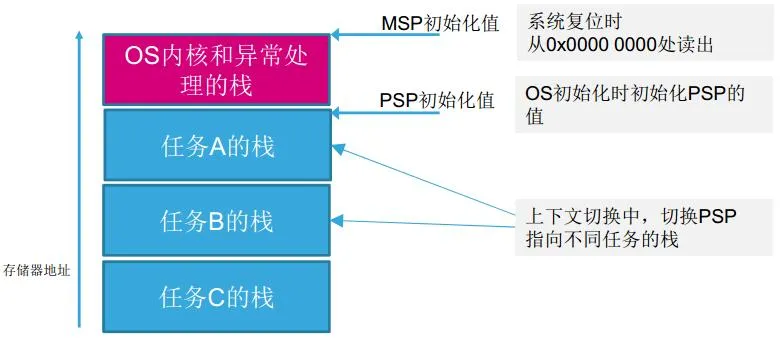
初始化时的操作
- 系统复位时从0x00000000处读出MSP的初始值。
- 在OS初始化时，对PSP进行初始化。
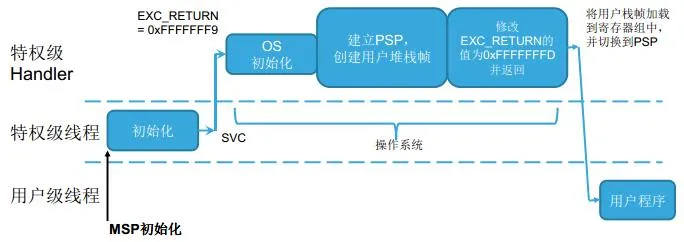
任务调度时的操作
- 用任务A的SP执行入栈操作，并保存任务A的SP。
- 设置PSP指向任务B的栈空间，用任务B的SP执行出栈，随后开始执行任务B。
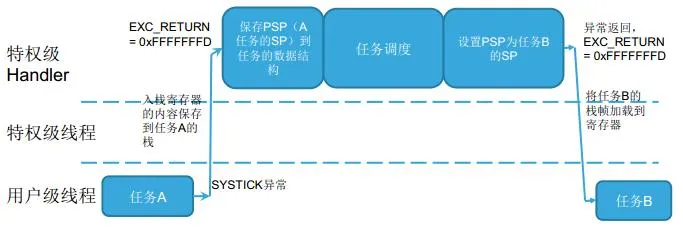
用户级和特权级
Cortex-M分为两个运行级别
处理模式：异常与中断，工作在特权级
线程模式：其他情况，可以工作在用户级和特权级
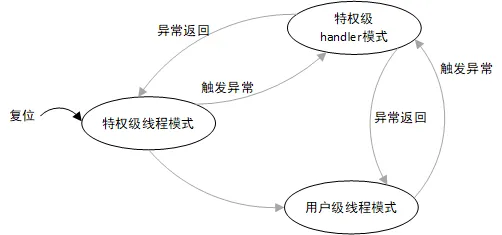
NVIC（嵌套向量中断控制器）
NVIC支持中断嵌套功能。当一个中断触发并且系统进行响应时，处理器硬件会将当前运行位置的上下文寄存器自动压入中断栈中，这部分的寄存器包括 PSR、PC、LR、R12、R3-R0 寄存器
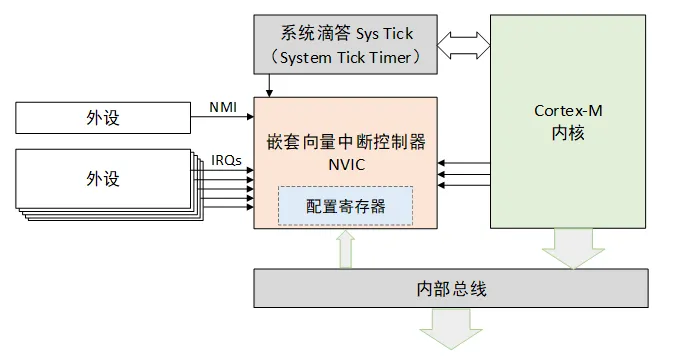
M3 M4对比
M4新增FPU浮点
相较于M3用软件方式计算浮点，硬件浮点计算更快
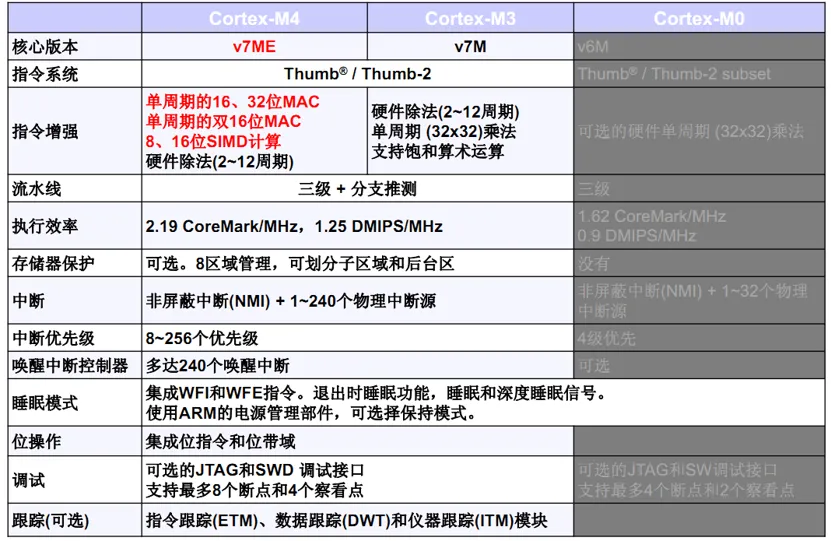
基础、语法
static关键字
【在函数体内】，【修饰局部变量】，其访问权限在函数内，仅初始化一次，存储于静态存储区（可通过其地址，在其他文件中访问修改，BUG！！！）
【在模块内，函数体外】，【修饰全局变量】将模块的全局变量限制在模块内部（仅供.c使用），不能跨文件共享
【在模块内】，【修饰函数】，该函数仅可被本模块调用，不能作为接口暴露给其他模块
注意：static 与 extern不可同时修饰一个变量
const关键字
变量一旦被初始化后无法修改。
常量指针与指针常量，* (指针）和 const（常量） 谁在前先读谁 ；*象征着地址，const象征着内容；谁在前面谁就不允许改变。
cint * const p; //a是一个指向整型数的常指针（指针指向不可以修改，整型数（指针指向的值）可以修改）（指针常量）
<==>const p
// const 修饰指针p
*p=10; // 指针指向的值可以修改
// p=&b; // 指针指向被限定
const int *p; //a是一个指向常整型数的指针（指针指向可以修改，整型数（指针指向的值）不可修改）（常量指针）
<==>const *p
// const 修饰*p
// *p=10; // 指针指向的值被限定
p=&b; // 指针指向可以修改
const int * const a; //a是一个指向常整形数的常指针（都不可修改）
void printArray(const int *arr, int size) //防止修改入参
const char* getString() //防止修改返回值，返回值为指针的时候
volatile关键字
作用：每次从内存或对应外设寄存器中取值放入CPU寄存器通用寄存器后进行操作，防止编译器优化
详解：CPU读取数据时，会从指定地址处取值并搬运到CPU通用寄存器中处理，在不加volatile时，对于频繁的操作，编译器会将代码的汇编指令进行优化，例子如下：
c // 比如要往某一地址送两指令：
int *ip = 0x12345678; //设备地址
*ip = 1; //第一个指令
*ip = 2; //第二个指令
// 编译器可能优化为：
int *ip = 0x12345678; //设备地址
*ip = 2; //第二个指令
// 造成第一条指令被忽略
volatile int *ip = 0x12345678; //设备地址
*ip = 1; //第一个指令
*ip = 2; //第二个指令
场合：寄存器、临界区访问的变量、中断函数访问的全局或static变量
Note：与Cache的区别：
- volatile是对编译器的约束，可以控制每次从RAM读取到通用寄存器，但无法控制从RAM到通用寄存器的过程（从RAM到寄存器要经过cache）。若两次被volatile修饰的读取指令过快，即使RAM中的值改变了，但由于读取过快没有更新cache，那么实际上搬运到通用寄存器的值来自于cache，此类情况下需要禁用cache。
- 编译器优化是针对于LDR命令的，从内存中读取数据到寄存器时不允许优化这一过程，而None-cache保护的是对内存数据的访问（volatile无法控制LDR命令执行后是否刷新cache）
#define 与 const区别
| 名称 | 编译阶段 | 安全性 | 内存占用 | 调试 |
|---|---|---|---|---|
| #define | 编译的预处理阶段展开替换 | 低 | 占用代码段空间（.text） | 无法调试 |
| const | 编译、运行阶段 | 有数据类型检查 | 占用数据段空间（.data常量区） | 可调式 |
防止头文件重复引用
当程序中第一次 #include 该文件时，由于 _NAME_H 尚未定义，所以会定义 _NAME_H 并执行“头文件内容”部分的代码；当发生多次 #include 时，因为前面已经定义了 _NAME_H，所以不会再重复执行“头文件内容”部分的代码。
c#ifndef _NAME_H
#define _NAME_H
//头文件内容
#endif
函数调用与栈、寄存器
cvoid fun(int a, int b);
fun(1, 2); // 调用函数时，入栈顺序为参数从右往左，从而取参数时从左往右
| 1 |
| 2 |
——
右边的参数先入栈，存放在R0-R3中，多余4个的参数存放在任务栈中
返回值在R0寄存器
全局变量和局部变量区别
全局变量存储在静态存储区，局部变量存储在栈中
堆栈溢出原因
动态内存分配后未正确回收，内存泄漏
函数递归调用深度太深，栈深度不够
局部变量与全局变量重名
局部变量在栈中；全局变量在静态存储区
局部变量作用域在{}内，就近原则
访问内存中某地址数据
c// 读取
int result=*(int *)0x123456; // 方法1
int *ptr=const(int *)0x123456; // 方法2
int result=*ptr;
// 修改
*(int * const)(0x56a3) = 0x3344; // 方法1
int * const ptr = (int *)0x56a3; // 方法2
*ptr = 0x3344;
枚举类型
cenum DAY {
MON=1, TUE, WED, THU, FRI, SAT, SUN
};
int main() {
enum DAY day;
day = WED;
printf("%d",day); // 3
return 0;
}
enum COLOR {
black, // 默认为0
white, // 默认+1
red
}；
enum COLOR {
black = 1, // 手动指定起始值
white,
red
}；
enum COLOR {
black, // 0
white = 3,
red // 4
}；
float精度
- float的精度是保证至少7位有效数字是准确的
- float的取值范围[-3.4028235E38, 3.4028235E38]，精确范围是[-340282346638528859811704183484516925440, 340282346638528859811704183484516925440]
(1条消息) float的精度和取值范围_float精度_AlbertS的博客-CSDN博客
结构体字节对齐
字节对齐的作用就是规定数据在内存中的存储起始地址必须是某个特定字节数（通常是数据类型的大小）的整数倍。
1.读取效率问题
以32位机为例，它每次取32个位，也就是4个字节。以int型数据为例，如果它在内存中存放的位置按4字节对齐，也就是说1个int的数据全部落在计算机一次取数的区间内，那么只需要取一次就可以了。如图2-1。如果访问未对齐的内存，处理器需要作两次内存访问，很不巧，这个int数据刚好跨越了取数的边界，这样就需要取两次才能把这个int的数据全部取到，如图2-2，这样效率也就降低了
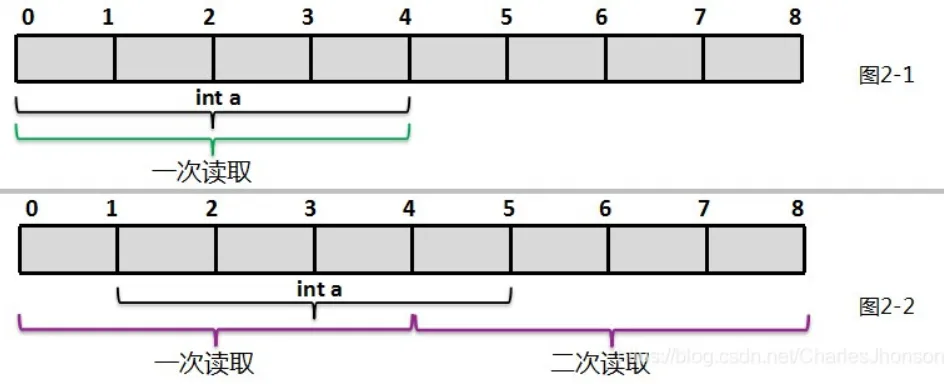
2.存储空间占用
排列顺序不同时占用空间也不同
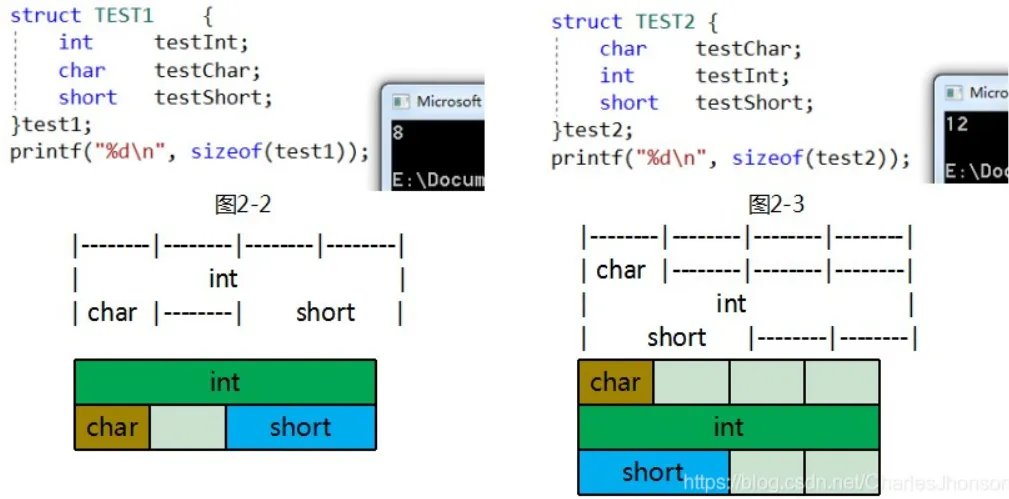
结构体嵌套时
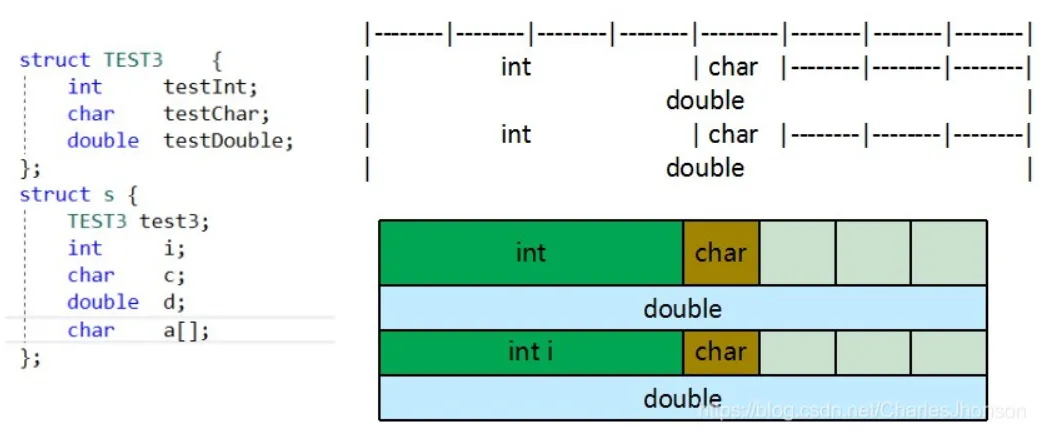
3. 实际使用
c++#pragma pack (n) // 编译器将按照n个字节对齐；
#pragma pack() // 恢复先前的pack设置,取消设置的字节对齐方式
#pragma pack (1) // 1字节对齐
typedef struct TestNoAlign {
unsigned char u8_test1; // 1
unsigned int u32_test2; // 4
double d8_test3; // 8
}TestNoAlign;
#pragma pack () // 取消
typedef struct TestAlign {
unsigned char u8_test1; // 1+3
unsigned int u32_test2; // 4
double d8_test3; // 8
}TestAlign;
int main(void)
{
printf("sizeof(TestNoAlign) is %d sizeof(TestAlign) is %d \n",
sizeof(TestNoAlign),sizeof(TestAlign));
return 0;
}
// 13 & 16
联合体
在同一地址空间中存储不同类型的数据
ctypedef union test_u{
int a;
char b;
}test;
test t;
t.a = 0x12345678;
if(t.b == 0x78) {
printf("小端\n"); // 低地址0x00000000 放低字节0x78
}
else {
printf("大端\n"); // 低地址0x00000000 放高字节0x12
}
实际使用：分离高低字节
cunion div
{
int n; // n中存放要进行分离高低字节的数据
char a[4]; // 一个整形占两个字节，char占一个字节，a[2]将n分为了两部分
}test;
test.n = 0x12345678; // 寄存器赋值
TH1 = test.a[0]; // test.a[0]中存储的是低位数据 0x78
TL1 = test.a[3]; // test.a[1]中储存了test.n的高位数据 0x12
实际使用：寄存器定义与位域
cunion test {
uint32_t reg;
struct {
uint32_t reserve:4; // 占用低字节的4bit
uint32_t ctrl:4;
uint32_t enable:5;
uint32_t dis:3;
uint32_t stat:1;
uint32_t loop:7;
uint32_t ext:2;
uint32_t mode:6; // 位域和为32
}bits;
};
int main(void) {
union test mytest;
mytest.reg = 0xa5a5a5a5;
printf("reg value=0x%x\n", mytest.reg);
printf("reserve(3:0)=0x%x\n", mytest.bits.reserve);
printf("ctrl(7:4)=0x%x\n", mytest.bits.ctrl);
printf("enable(12:8)=0x%x\n", mytest.bits.enable);
printf("dis(15:13)=0x%x\n", mytest.bits.dis);
printf("stat(16:16)=0x%x\n", mytest.bits.stat);
printf("loop(23:17)=0x%x\n", mytest.bits.loop);
printf("ext(25:24)=0x%x\n", mytest.bits.ext);
printf("mode(31:26)=0x%x\n", mytest.bits.mode);
return 0;
}
取u32的某一字节
c// 方法1
union bit32_data {
uint32_t data;
struct {
uint8_t byte0;
uint8_t byte1;
uint8_t byte2;
uint8_t byte3;
}byte;
};
union bit32_data num;
num.data = 0x12345678;
printf("byte0 = 0x%x\n", num.byte.byte0);
printf("byte1 = 0x%x\n", num.byte.byte1);
printf("byte2 = 0x%x\n", num.byte.byte2);
printf("byte3 = 0x%x\n", num.byte.byte3);
// 方法2
#define GET_LOW_BYTE0(x) ((x >> 0) & 0x000000ff) /* 获取第0个字节 */低
#define GET_LOW_BYTE1(x) ((x >> 8) & 0x000000ff) /* 获取第1个字节 */
#define GET_LOW_BYTE2(x) ((x >> 16) & 0x000000ff) /* 获取第2个字节 */
#define GET_LOW_BYTE3(x) ((x >> 24) & 0x000000ff) /* 获取第3个字节 */高
unsigned int a = 0x12345678;
printf("byte0 = 0x%x\n", GET_LOW_BYTE0(a));
printf("byte1 = 0x%x\n", GET_LOW_BYTE1(a));
printf("byte2 = 0x%x\n", GET_LOW_BYTE2(a));
printf("byte3 = 0x%x\n", GET_LOW_BYTE3(a));
strcmp
字符串1＝字符串2，返回值＝0； 字符串2〉字符串2，返回值〉0； 字符串1〈字符串2，返回值〈0。
位操作
c#define GetBit(x , bit) (((x) & (1 << (bit)) >> (bit)) // 获取将x的第y位（0或1）先左移再右移
#define SetBit(x , bit) ((x) |= (1 << (bit)) // 将X的第Y位置1
#define ClrBit(x , bit) ((x) &= ~(1 << (bit)) // 将X的第Y位清0
寄存器操作
ctypedef union Reg
{
u32 Byte;
struct
{
u32 a : 16; // bit [0-15]
u32 b : 8; // bit [16-23]
u32 c : 1; // bit 24
u32 d : 4; // bit[25-28]
u32 e : 1; // bit29
u32 f : 1; // bit30
u32 g : 1; // bit31
};
} Reg; // 占用u32大小空间
// usage
int main()
{
Reg misc;
misc.u32 = 0xffff0000;
misc.a = 0xaa;
printf("0x%x\n", misc.u32);
return 0;
}
// 执行结果：0xffff00aa
运算符优先级
如果一个表达式中的两个操作数具有相同的优先级，那么它们的结合律（associativity）决定它们的组合方式是从左到右或是从右到左。
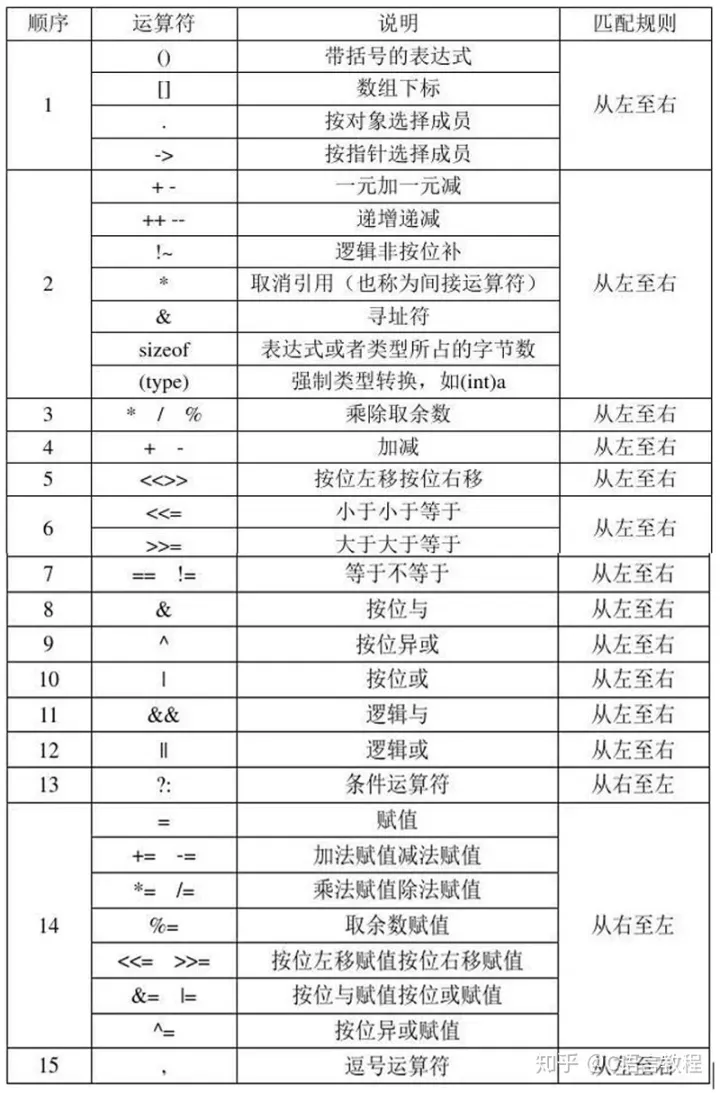
*ptr++
cint num[] ={1,3,5,7,9};
int* ptr_num = num;
cout << *++ptr_num << endl;
//输出为 3
// 先对指针移位地址加1，然后解引用
cout << ++*ptr_num << endl;
// 输出为2
// 先解引用，再对数值+1
cout<< *ptr_num++ << " , "<< *ptr_num <<endl;
// 输出 1,3
// *与++优先级相同，右边线运算，但因为是后++，因此先解引用输出1，然后对指针++，指向第二个元素
cout << (*ptr_num)++ << " , "<< num[0] <<endl;
// 输出1,2
// 先解引用取指，修改值++
int a[5] = {0, 1, 2, 3, 4};
int *ptr = a;
printf("%d\n", *ptr);
printf("%d\n", *ptr++);
printf("%d\n", *ptr);
printf("%d\n", *++ptr);
printf("%d\n", *ptr);
// 0 0 1 2 2
常用情景
cunsigned char Get_CRC8_Check_Sum(unsigned char *pchMessage, unsigned int dwLength, unsigned char ucCRC8) {
unsigned char ucIndex;
while (dwLength --) {
ucIndex = ucCRC8^(*pchMessage++); // 先取指针的指向的值，使用完后指针自增
ucCRC8 = CRC8_TAB[ucIndex];
}
return(ucCRC8);
}
类型转换小Trick
将uint32_t数据赋值到uint8_t数组中：
cuint32_t data = 123;
uint8_t databuf[4] = {0};
*( (uint32_t *)databuf ) = data;//等价于memcpy(databuf, &data, 4);
比较浮点数
c++// float 4byte
abs(a-b) < 0.00001 1e^-5;
// double 8byte
// 判断阈值更小，16位左右
指针、数组指针、指针数组、函数指针
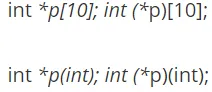
cint *p[10]; // 一个数组，存放有10个指针
int (*p)[10]; // 一个指针，指向长度为10的数组
int *p(int); // 一个函数，返回int*指针
int (*p)(int); // 一个函数指针，函数参数int，返回值int
int* (*a[10])(int) // 一个数组，存放10个函数指针
c// 第二种的用法举例
int a[][3]={{1,2,3},{4,5,6}};
int (*p)[3];
p=a;
// 这时，p指向元素1，p+1就指向元素4
// *（*（p+1）+2）就等价于a[1][2]这个元素值
函数指针与回调函数
c// 回调函数案例1
int callback_1(void) { //回调函数1主体
printf("call_1\n");
return 0;
};
int callback_2(void) { //回调函数2主体
printf("call_2\n");
return 0;
};
//定义一个处理函数，传入的是函数指针
int Handle(int (*callback)(void)) {
callback(); // 调用函数
}
int main()
{
//定义两个函数指针来指向函数地址
//不定义也可以，因为函数名称本身就是函数入口地址
int (*call1)(void) = &callback_1;
int (*call2)(void) = &callback_2;
Handle(call1); // 函数指针当参数调用
Handle(call2);
call1(); // 也可直接调用
//改变函数指针指向
call1=&callback_2;
Handle(call1);
return 0;
}
c++int max(int a, int b) {
return a > b ? a : b;
}
int min(int a, int b) {
return a < b ? a : b;
}
int (*f)(int, int); // 声明函数指针，指向返回值类型为int，有两个参数类型都是int的函数
int main(int argc, _TCHAR* argv[])
{
f = max; // 函数指针f指向求最大值的函数max
int c = (*f)(1, 2);
printf("The max value is %d \n", c);
f = min; // 函数指针f指向求最小值的函数min
c = (*f)(1, 2);
printf("The min value is %d \n", c);
return 0;
}
c// 结构体封装函数指针
struct DEMO
{
int x,y;
int (*func)(int,int); //函数指针
};
int add2(int x,int y)
{
return x+y;
}
void main()
{
struct DEMO demo;
demo.func = &add2; //结构体函数指针赋值
demo.func = add2; //这样写也可以
int ans = demo.func(3,4); // 调用
}
隐式类型转换
C 语言中不同类型的数据需要转换成同一类型，才可以计算
发生情况：
c// 赋值转换，可能造成精度降低，不安全
double pi = 3.14;
int num = pi;
转换规则：
-
转换按照数据长度增加的方向进行，以保证精度不降低。如 int 和 double相加时，int 会被隐式转换成 double 类型
-
如果两种类型的字节数一样，且一种有符号，另一种无符号，则转换成无符号类型（例如下）
-
char 类型和 short 类型参与运算时，必须先转换成 int 类型（整型提升）
c++unsigned int a = 6;
int b = -20;
int c;
((a+b) > 6) ? (c=1):(c=0);
//输出是0
存在unsigned且数据长度一致时，会将有符号类型隐私转换为无符号类型（负数存在问题）
二维数组
内存模型：按行优先存储
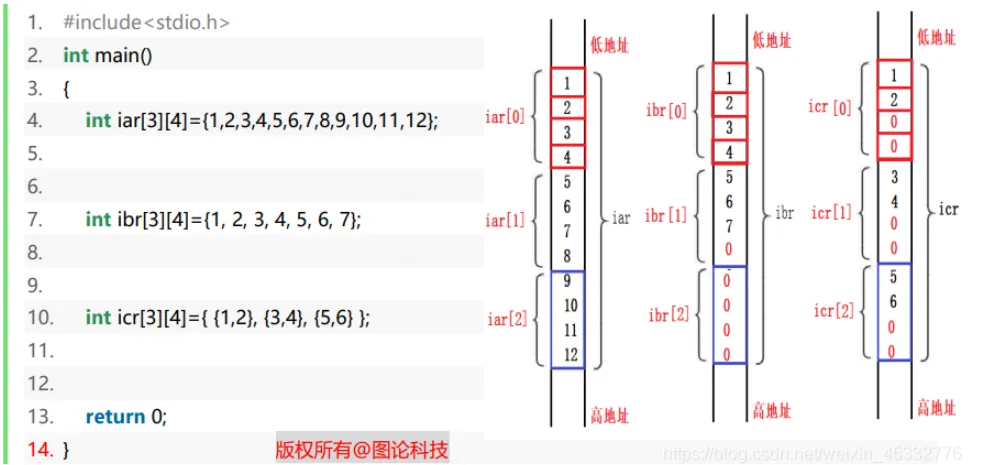
cint Arr [3] [4] = {{1,1,1,1},{2,2,2,2},{3,3,3,3},{4,4,4,4}};
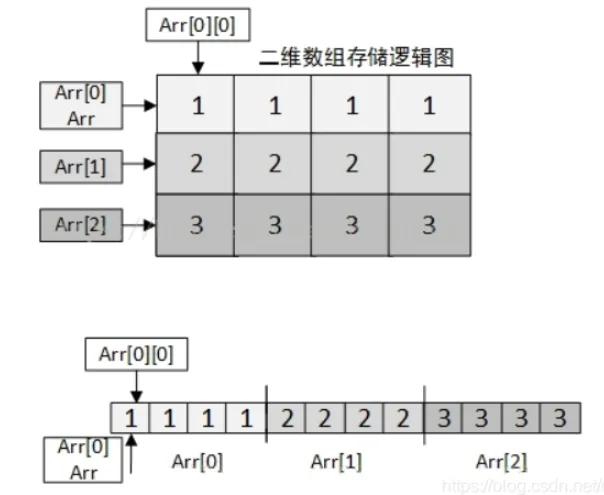
数组地址+1
c// 一维数组
int a[5]={1,2,3,4,5};
int * ptr=(int*)(&a+1); // &a为整个数组的地址，&a+1为数组整体大小后移的位置
*(ptr-1) // 为数组最后一个元素的大小，=5
a++; // 非法，a虽然是指向数组首地址的指针，但其实际为cosnt类型，指针的指向无法改变
int* p = a; p++; // 这样合法
// 二维数组
int a[2][3] = {1,3,5,7,9,11};
**(a+1) = 7 // *(a+1)为a[0]+1，是第二行的首地址
双指针数组int **a[3][4]
c++int *z[3];
int **zz[3][4];
std::cout << sizeof(z) << std::endl;
std::cout << sizeof(zz) << std::endl;
//输出 3*8=24 与 4*24=96
int *array[10];
函数声明：void fun(int *a[10]);
函数调用：fun(array);
访问：使用*(a[i]+j)访问数组中的元素
int **array[10][20];
函数声明：void fun(int **a[10][20]);
函数调用：fun(array);
访问：(*(a+i) + j) 或者a[i][j]访问元素（使用双重指针表示的二维数组的访问方法）
[(22条消息) 二维数组与双重指针_Ven_J的博客-CSDN博客_双重指针数组](https://blog.csdn.net/Arcofcosmos/article/details/113645091)
二级指针
cvoid get(char** p, int num) {
*p = (char*)malloc(sizeof(char) * num);
}
char *str;
get(&str,10);
strcpy(str, "hello");
std::cout << str << std::endl;
cvoid get(char* p, int num) {
p = (char*)malloc(sizeof(char) * num);
}
char *str;
get(str,10);
strcpy(str, "hello");
std::cout << str << std::endl;
//ERROR
要改变指针指向的值，传入指针
要改变指针的指向，需要传入二级指针
register关键字
在 C++ 中，register 是一种关键字，用于建议编译器将变量存储在寄存器中，以提高访问速度。然而，需要注意的是，自 C++11 标准开始，register 关键字已经被弃用，编译器会忽略该建议。
在早期的 C++ 标准中，register 关键字可以用于声明变量，以提示编译器将其存储在寄存器中。寄存器是位于 CPU 内部的一种高速内存，可以更快地访问其中的数据，而不需要像访问内存地址那样的开销。通过存储在寄存器中，可以提高对变量的访问速度，从而提高程序的性能。
使用 register 关键字声明变量并不意味着变量一定会被存储在寄存器中，它只是向编译器提出了一个建议。编译器会根据具体的情况（如寄存器的可用性、变量的作用域等）决定是否将变量存储在寄存器中。如果编译器无法满足这个要求，那么该变量将按照通常的方式存储在内存中。
然而，需要注意的是，现代的编译器已经非常智能化，能够基于自身的优化算法和对代码的分析，自动决定何时将变量存储在寄存器中，而无需开发人员使用 register 关键字进行提示。因此，即使使用 register 关键字，编译器也可以忽略它，根据自身的优化策略来选择最佳的存储方式。
综上所述，register 关键字是一种用于建议编译器将变量存储在寄存器中的关键字，但自 C++11 标准开始已经被弃用，编译器会忽略它。现代编译器已经能够自动进行寄存器分配和优化，所以在实际编程中不再需要使用 register 关键字。
sizeof()
- sizeof 是在编译的时候，查找符号表，判断类型，然后根据基础类型来取值。
- 如果 sizeof 运算符的参数是一个不定长数组，则该需要在运行时计算数组长度。
字符设备与块设备
字符设备：操纵并读取硬件状态
块设备：存储功能，写入数据再读取，数据传输单位是扇区
extern”C” 的作用
实现C++中正确调用C编写的模块
32Bit 64Bit区别
CPU 通用寄存器的数据宽度（CPU 一次能并行处理的二进制位数）
寻址能力（32Bit仅支持4GB寻址）
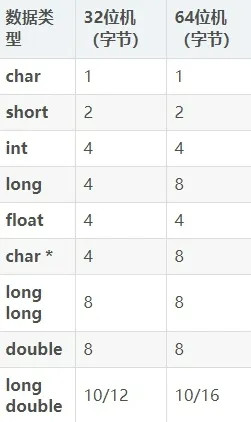
大小端
STM32：小端，低地址存放低位0x12345678：低->高78 56 34 12
| 大端 | 小端 | |
|---|---|---|
| 存储方式 | 高位存在低地址 | 高位存在高地址 |
| 内存排布0x12345678 | 低地址-高地址 | 低地址-高地址 |
| 12 34 56 78 | 78 56 34 12 |
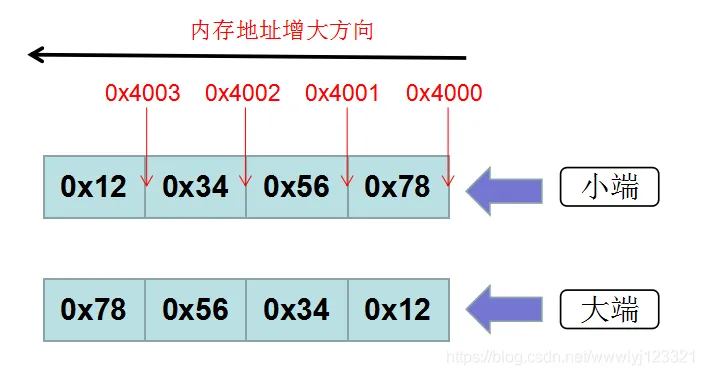判断方法
c#include<stdio.h>
union Un{
int a;
char b;
};
int is_little_endian1(void) {
union Un un;
un.a = 0x12345678;
if(un.b == 0x78) printf("小端\r\n");
else printf("大端\r\n");
}
int is_little_endian2(void) {
int a = 0x12345678;
char b = *((char *)(&a)); // 指针方式其实就是共用体的本质
if(b == 0x78) printf("小端\r\n");
else printf("大端\r\n");
}
转换方法
c// 变为u8类型数组后位移拼接
static inline uint32_t lfs_fromle32(uint32_t a) {
return (((uint8_t*)&a)[0] << 0) |
(((uint8_t*)&a)[1] << 8) |
(((uint8_t*)&a)[2] << 16) |
(((uint8_t*)&a)[3] << 24);
}
段错误
在LIinux 下C/C++中，出现段错误很多都是有指针造成的，段错误segmentation fault，信号SIGSEGV，是由于访问内存管理单元MMU异常所致，通常由于无效内存引用，如指针引用了一个不属于当前进程地址空间中的地址，操作系统便会进行干涉引发SIGSEGV信号产生段错误。
- 空指针（尝试操作地址为0的内存区域）
- 野指针（访问的内存不合法或无法察觉破坏了数据）
- 堆栈越界（同上）
- 修改了只读数据
为什么局部变量未定义时，每次初始化的结果是不确定的？
定义局部变量,其实就是在栈中通过移动栈指针,来给程序提供一个内存空间和这个局部变量名绑定。因为这段内存空间在栈上,而栈内存是反复使用的(脏的,上次用完没清零的) ,所以说使用栈来实现的局部变量定义时如果不初始化,里面的值就是一个垃圾值。
printf返回值
printf的返回值就是输出的字符数量‘
可变长度数组
VLA wariable length array
在C99中，允许在函数内部（栈空间）定义可变长度数组
c void test_func(int len) {
int arr[len];
arr[0] = 1; // 不可在定义时初始化
}
test_func(3);
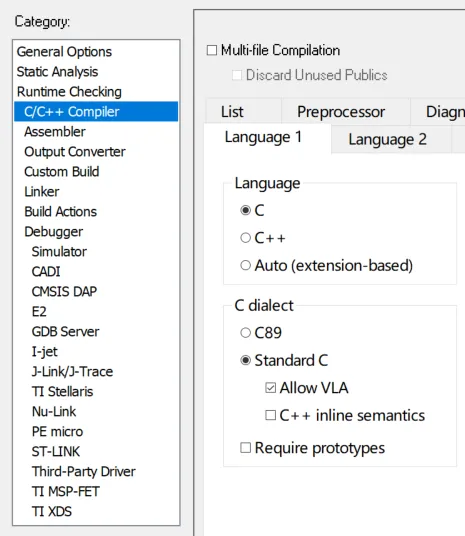
变长结构体
在结构体中定义长度为0的数组，用以后续开辟变长buf，释放时仅释放结构体即可
c++#include <stdafx.h>
#include <iostream>
using namespace std;
const int BUF_SIZE = 100;
struct s_one {
int s_one_cnt;
char* s_one_buf; // 用指针指向不定长buf
};
struct s_two {
int s_two_cnt;
char s_two_buf[0]; // 用数组指向不定长buf
};
int main()
{
//赋值用
constchar* tmp_buf = "abcdefghijklmnopqrstuvwxyz";
int ntmp_buf_size = strlen(tmp_buf);
//<1>注意s_one 与s_two的大小的不同
cout<< "sizeof(s_one) = " << sizeof(s_one) << endl; //8
cout<< "sizeof(s_two) = " << sizeof(s_two) << endl; //4
cout<< endl;
//为buf分配100个字节大小的空间
int ntotal_stwo_len = sizeof(s_two) + (1 + ntmp_buf_size) * sizeof(char);
//给s_one buf赋值
s_one* p_sone = (s_one*)malloc(sizeof(s_one)); // 开辟结构体
memset(p_sone, 0, sizeof(s_one));
p_sone->s_one_buf = (char*)malloc(1 + ntmp_buf_size); // 开辟buf
memset(p_sone->s_one_buf, 0, 1 + ntmp_buf_size);
memcpy(p_sone->s_one_buf, tmp_buf, ntmp_buf_size);
//给s_two buf赋值
s_two* p_stwo = (s_two*)malloc(ntotal_stwo_len); // 开辟结构体
memset(p_stwo, 0, ntotal_stwo_len);
memcpy((char*)(p_stwo->s_two_buf), tmp_buf, ntmp_buf_size); //不用加偏移量，直接拷贝!
cout<< "p_sone->s_one_buf = " << p_sone->s_one_buf<< endl;
cout<< "p_stwo->s_two_buf = " << p_stwo->s_two_buf<< endl;
cout<< endl;
//<2>注意s_one 与s_two释放的不同！
if(NULL != p_sone->s_one_buf) { // 用指针保存需要释放两次
free(p_sone->s_one_buf); // 释放指针
p_sone->s_one_buf= NULL;
if(NULL != p_sone) {
free(p_sone); // 释放结构体
p_sone= NULL;
}
cout<< "free(p_sone) successed!" << endl;
}
if(NULL != p_stwo) { // 结构体保存释放一次
free(p_stwo); // 仅释放结构体
p_stwo= NULL;
cout<< "free(p_stwo) successed!" << endl;
}
return0;
}
CRC校验
循环冗余校验
一个完整的CRC参数模型应该包含以下信息：WIDTH，POLY，INIT，REFIN，REFOUT，XOROUT。通常如果只给了一个多项式，其他的没有说明则：INIT=0x00，REFIN=false，REFOUT=false，XOROUT=0x00。
- NAME：参数模型名称。
- WIDTH：宽度，即生成的CRC数据位宽，如CRC-8，生成的CRC为8位
- POLY：十六进制多项式，省略最高位1，如 x8 + x2 + x + 1，二进制为1 0000 0111，省略最高位1，转换为十六进制为0x07。
- INIT：CRC初始值，和WIDTH位宽一致。
- REFIN：true或false，在进行计算之前，原始数据是否翻转，如原始数据：0x34 = 0011 0100，如果REFIN为true，进行翻转之后为0010 1100 = 0x2c
- REFOUT：true或false，运算完成之后，得到的CRC值是否进行翻转，如计算得到的CRC值：0x97 = 1001 0111，如果REFOUT为true，进行翻转之后为11101001 = 0xE9。
- XOROUT：计算结果与此参数进行异或运算后得到最终的CRC值，和WIDTH位宽一致。
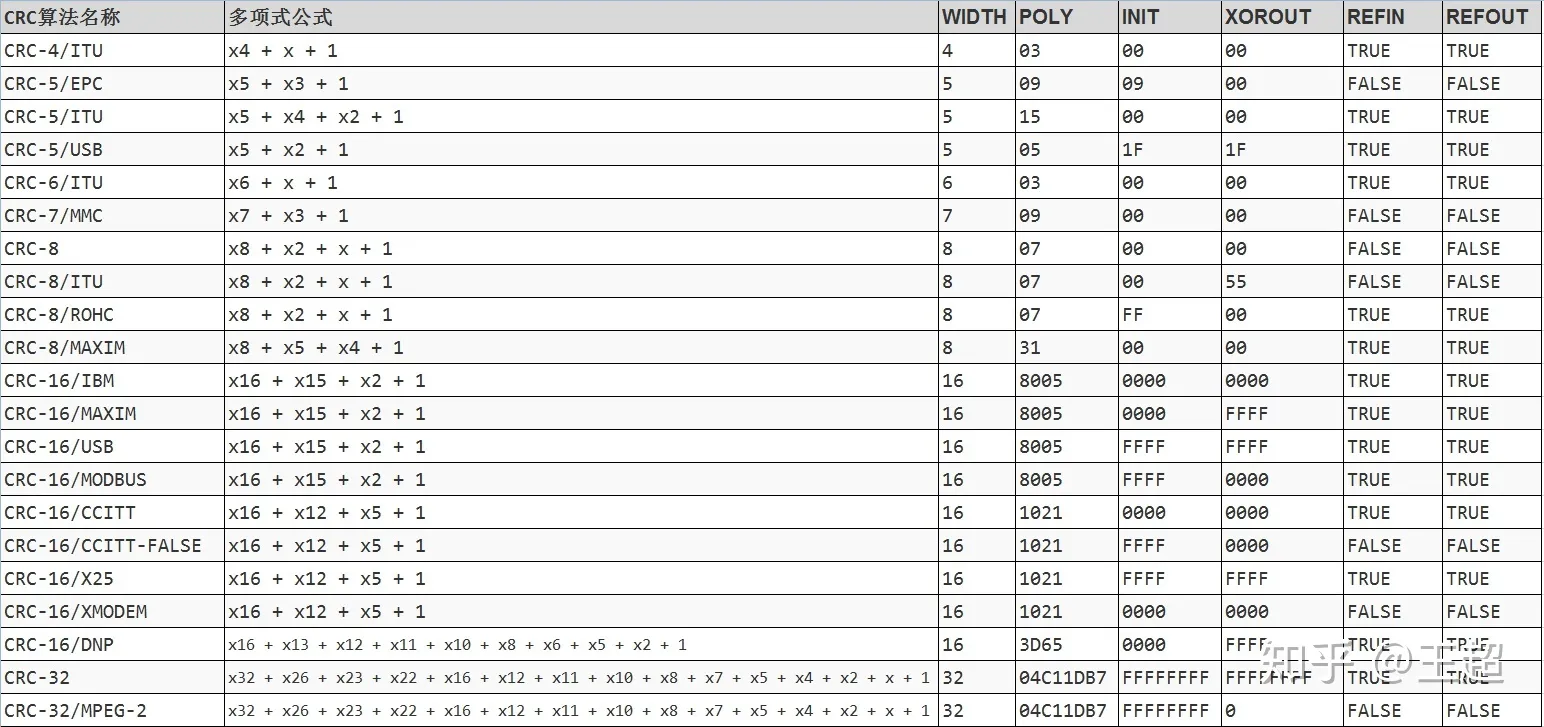使用方法：
c#include "crcLib.h"
int main() {
uint8_t LENGTH = 10;
uint8_t data[LENGTH];
uint8_t crc;
for(int i = 0; i < LENGTH; i++) {
data[i] = i*5;
printf("%02x ", data[i]);
}
printf("\n");
crc = crc8_maxim(data, LENGTH);
printf("CRC-8/MAXIM:%02x\n", crc);
return 0;
}
c//crc8 generator polynomial:G(x)=x8+x5+x4+1
const unsigned char CRC8_INIT = 0xff;
const unsigned char CRC8_TAB[256] = {
0x00, 0x5e, 0xbc, 0xe2, 0x61, 0x3f, 0xdd, 0x83, 0xc2, 0x9c, 0x7 e, 0x20, 0xa3, 0xfd, 0x1f, 0x41,
0x9d, 0xc3, 0x21, 0x7f, 0xfc, 0xa2, 0x40, 0x1e, 0x5f, 0x01, 0xe3, 0xbd, 0x3e, 0x60, 0x82, 0xdc, 0x23,
0x7d, 0x9f, 0xc1, 0x42, 0x1c, 0xfe, 0xa0, 0xe1, 0xbf, 0x5d, 0x03, 0x80, 0xde, 0x3c, 0x62, 0xbe, 0xe0,
0x02, 0x5c, 0xdf, 0x81, 0x63, 0x3d, 0x7c, 0x22, 0xc0, 0x9e, 0x1d, 0x43, 0xa1, 0xff, 0x46, 0x18, 0xfa,
0xa4, 0x27, 0x79, 0x9b, 0xc5, 0x84, 0xda, 0x38, 0x66, 0xe5, 0xbb, 0x59, 0x07, 0xdb, 0x85, 0x67,
0x39, 0xba, 0xe4, 0x06, 0x58, 0x19, 0x47, 0xa5, 0xfb, 0x78, 0x26, 0xc4, 0x9a , 0x65, 0x3b, 0xd9, 0x87,
0x04, 0x5a, 0xb8, 0xe6, 0xa7, 0xf9, 0x1b, 0x45, 0xc6, 0x98, 0x7a, 0x24, 0xf8, 0xa6, 0x44, 0x1a, 0x99,
0xc7, 0x25, 0x7b, 0x3a, 0x64, 0x86, 0xd8, 0x5b, 0x05, 0xe7, 0xb9,
0x8c, 0xd2, 0x30, 0x6e, 0xed, 0xb3, 0x51, 0x0f, 0x4e, 0x10, 0 xf2, 0xac, 0x2f, 0x71, 0x93, 0xcd, 0x11,
0x4f, 0xad, 0xf3, 0x70, 0x2e, 0xcc, 0x92, 0xd3, 0x8d, 0x6f, 0x31, 0xb2, 0xec, 0x0e, 0x50, 0xaf, 0xf1,
0x13, 0x4d, 0xce, 0x90, 0x72, 0x2c, 0x6d, 0x33, 0xd1, 0x8f, 0x0c, 0x52, 0xb0, 0xee, 0x32, 0x6c, 0x8e,
0xd0, 0x53, 0x0d, 0xef, 0xb1, 0xf0, 0xae, 0x4c, 0x12, 0x91, 0xcf, 0x2d, 0x73, 0xca, 0x94, 0x76, 0x28,
0xab, 0xf5, 0x17, 0x49, 0x08, 0x56, 0xb4, 0xea, 0x69, 0x37, 0xd5, 0x8b, 0x57, 0x09, 0xeb, 0xb5,
0x36, 0x68, 0x8a, 0xd4, 0x95, 0xcb, 0x29, 0x77, 0xf4, 0xaa, 0x48, 0x1 6, 0xe9, 0xb7, 0x55, 0x0b, 0x88,
0xd6, 0x34, 0x6a, 0x2b, 0x75, 0x97, 0xc9, 0x4a, 0x14, 0xf6, 0xa8,
0x74, 0x2a, 0xc8, 0x96, 0x15, 0x4b, 0xa9, 0xf7, 0xb6, 0xe8, 0x0a, 0x54, 0xd7, 0x89, 0x6b, 0x35,
}
// 计算CRC值
unsigned char Get_CRC8_Check_Sum(unsigned char *pchMessa ge, unsigned int dwLength, unsigned char ucCRC8) {
unsigned char ucIndex;
while (dwLength --) {
ucIndex = ucCRC8^(*pchMessage++);
ucCRC8 = CRC8_TAB[ucIndex];
}
return(ucCRC8);
}
// 验证CRC值
/*
** Descriptions: CRC8 Verify function
** Input: Data to Verify,Stre am length = Data + checksum
** Output: True or False (CRC Verify Result)
*/
unsigned int Verify_CRC8_Check_Sum(unsigned char *pchMessage, unsigned int dwLength) {
unsigned char ucExpected = 0;
if ((pchMessage == 0) || (dwLength <= 2)) return 0;
ucExpected = Get_CRC8_Check_Sum (pchMessage, dwLength 1, CRC8_INIT);
return ( ucExpected == pchMessage[dwLength-1] );
}
/*
** Descriptions: append CRC8 to the end of data
** Input: Data to CRC and append,Stream length = Data + checksum
** Output: True or False (CRC Verify Result)
*/
void Append_CRC8_Check_Sum(unsigned char *pchMessage, unsigned int dwLength) {
unsigned char ucCRC = 0;
if ((pchMessage == 0) || (dwLength <= 2)) return;
ucCRC = Get_CRC8_Check_Sum ( (unsigned char *)pc hMessage, dwLength 1, CRC8_INIT);
pchMessage[dwLength 1] = ucCRC;
uint16_t CRC_INIT = 0xffff;
}
奇偶校验
如果数据中1的个数为奇数，则奇校验位0，否则为1
例：1101中，1有3个，校验码为0
静态链接与动态链接
静态库在链接阶段的进行组合，动态库在运行时加载
静态链接生成的可执行文件体积较大，消耗内存，如果所使用的静态库发生更新改变，程序必须重新编译
- 静态库的链接是将整个函数库的所有数据在编译时都整合进了目标代码，最小单位是文件，因此空间浪费，更新困难
- 动态库的链接是程序执行到哪个函数链接哪个函数的库
动态链接库编译时的操作：
我们在形成可执行程序时，发现引用了一个外部的函数，此时会检查动态链接库，发现这个函数名是一个动态链接符号，此时可执行程序就不对这个符号进行重定位，而把这个过程留到装载时再进行。
- 静态链接（Static Linking）：
- 在编译时将所有的函数和库代码合并成一个可执行文件。
- 链接是在编译段完成的，链接库和目标代码中提取所需的函数和库代码，将它们合并到最终的执行文件中 - 链接结果是一个独立的、完的可执行文件，包含了所有依赖的函数和库代码。
- 优点：
- 执行速度快，为所有代码已经被编译和链接在一起，无需运行时动态加载额外的库文件。
- 可执行文件独立，可以在没有安装相应库文件的系统上运行。
- 缺点：
- 可执行文件较，因为所有依赖的函数和库代码都被静态链接到可执行文件中。
- 更新和替换依赖的函数和库代码需要重新编译和链接整个程序。
- 动态链接（Dynamic Linking）：
- 在运行通过动态链接库在内存中加载所需的函数和库代码。
- 链接是在运行时完成的，链接器在运程序时动态加载所需的函数和库代码。
- 链接结果是一个可执行文件和一个或多个动态链接库，可执行文件只包含必要的启动代码和符号引用。
- 优点：
- 可执行文件较小，因为只包含必要的启动代码和符号引用。
- 动态链接库可以在多个可文件之间共享，节省内存空间。
- 更新和替换依赖的函数和库代码只需要替换对应的动态链接库。
- 缺点：
- 相对于静态链接，运行时需要额外的时间加载和解析动态链接库。 -中必须存在相应的动态链接库文件，否则程序无法运行。
总说，静态链接将所有的函数和库代码合并到一个可执行文件中，执行速度快，但可执行文件较大；而动态链接在运行时加载所需的函数和库代码，可执行文件较小，但可能需要额外的加载时间依赖系统存在相应的动态链接库文件。选择使用哪种方式取决于项目的需求和考虑的因素。
数据结构
二叉树遍历方式
- 先(根)序遍历（根左右）
- 中(根)序遍历（左根右）
- 后(根)序遍历（左右根）
链表操作
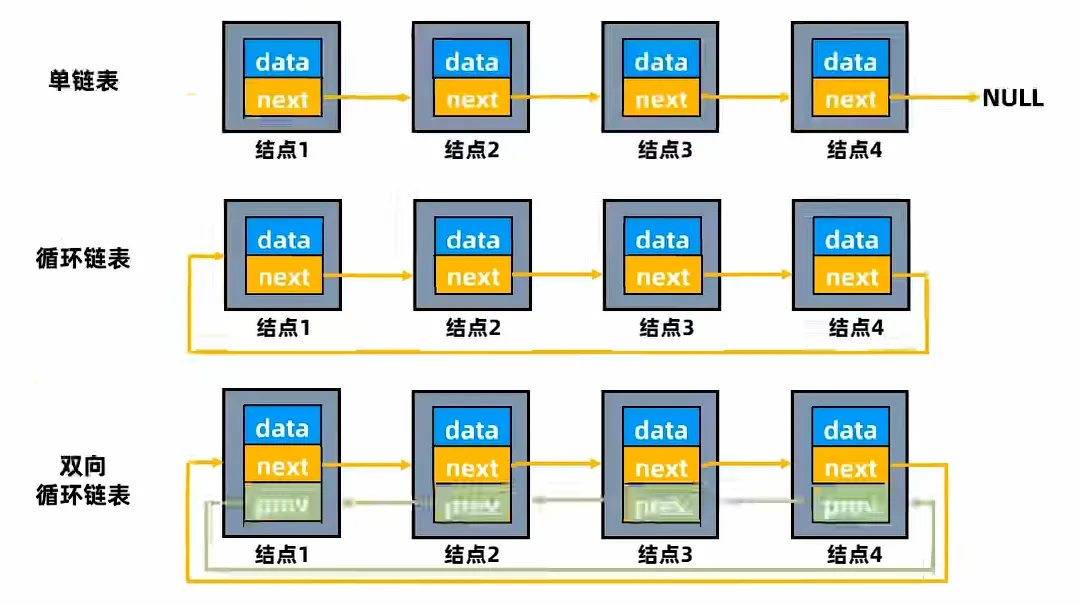
环形缓冲 循环队列
- 作用：FIFO，且写入数据为短时间大量，读取为低速少量但高频
- （平均读取速度一定要高于写入速度，否则多大的buf都会满）
- 主要构成：起始位置、长度、读位置、写位置
方法1：采用镜像指示位，读写越界时翻转镜像指示位
初始均为0，空；放入5个数据，读位置0不变，写位置+5后变为0+5=5
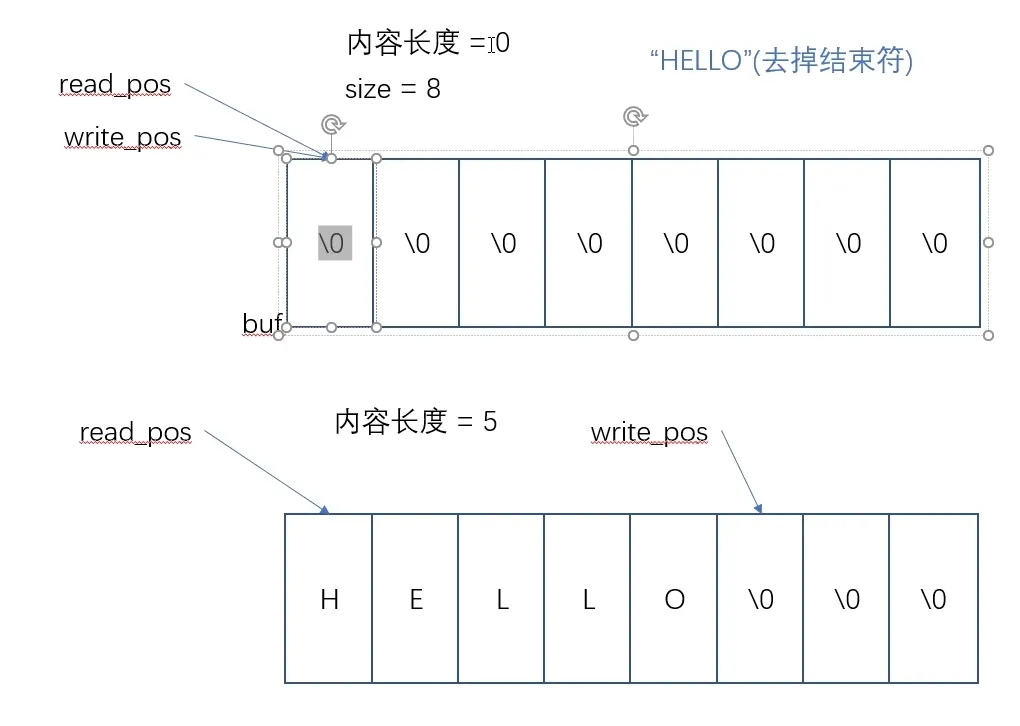尝试再次写入5个数据
此时镜像指示位write_mirror置1，表示越界了，同时读写指针均为0，表示满了
方法2：少利用一块数据区域，读写指针相等为空，写指针+1==读指针为满
ring buffer，一篇文章讲透它？ - 掘金 (juejin.cn)
c//队列为满的条件
(rear+1) % MaxSize == front;
//队列为空的条件
front == rear;
// 队列中元素的个数
(rear- front + maxSize) % MaxSize;
//入队
rear = (rear + 1) % maxSize;
// 出队
front = (front + 1) % maxSize;
当涉及到多线程时采用信号量通知，加锁互斥访问
通信协议
对比
| 协议 | 通信速率 | 优劣 | 工作模式 | 模块数量 | 接口数量 | 时序图 |
|---|---|---|---|---|---|---|
| UART | 115200 bit/s 约100 Kbit/s | 优势：双线制，全双工 劣势：时序要求严格，速率低 | 全双工，异步（依据约定波特率采样） | 一对一 | TX、RX | 起始位低电平，数据位8 bit（每Byte数据先发送低位），停止位以及空闲高电平，一帧10 bit  |
| 232 | 优势：规定了电气特性 劣势：传输距离15m，速率低 | 同UART | 一对一 | |||
| 485 | 优势：规定了电气特性，可组网，传输距离远1500m 劣势：半双工 | 半双工 | 一对多 | A、B |  | |
| IIC | 100或400 Kbit/s | 优势：双线制，低成本，有应答。 劣势：通信速率低，半双工，通信距离短 | 半双工，同步（起始信号，应答信号，结束信号） | 多主多从（谁控制时钟线谁为主设备）（器件地址唯一） | SDA、SCLK | 每Byte数据先发送高位，一帧9bit，SCLK（高电平读取，低电平发送）  |
| SPI | 10到150 Mbit/s | 优势：全双工高速，数据长度不限。 劣势：从机无应答信号，引脚较多，通信距离短 | 全双工，同步（拉低片选，依据时钟沿采样） | 一主多从（一、多根互斥的CS片选）（二、菊花链） | SCK、MOSI、MISO、CS | 每Byte数据先发送高位，帧长不限  |
| CAN | bx CAN：1Mbit/s CAN FD：8Mbit/s | 优势：差分电平通信距离长。 劣势：速率低带宽小 | 半双工 | 不分主从 | CANH、CANL |   |
UART
空闲时间总线高电平，起始位1bit拉低，数据位8bit，停止位1bit拉高
流控
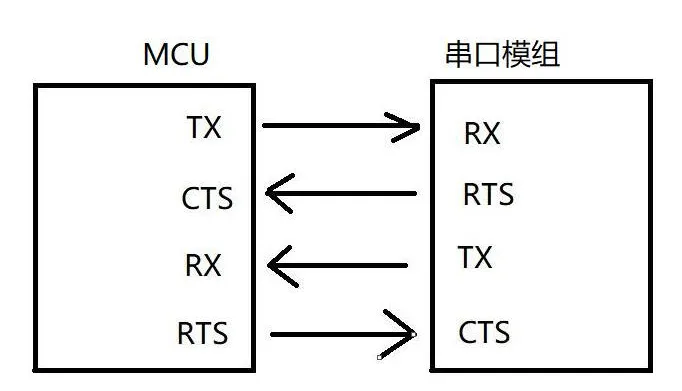
作用：当通信双方处理速度不一致时
接收方：通过RTS告知对方自己正在处理，占用时拉高（发送方等待），空闲时拉低（发送方发送）
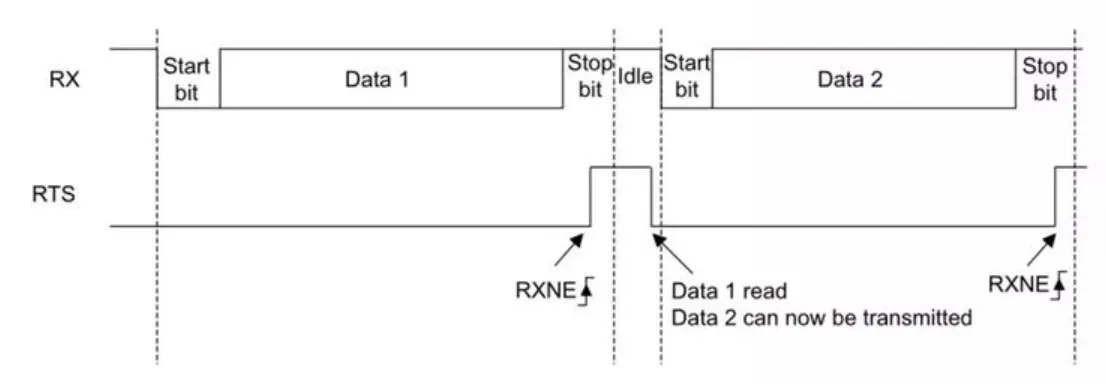
发送方：判断CTS信号，拉低时发送
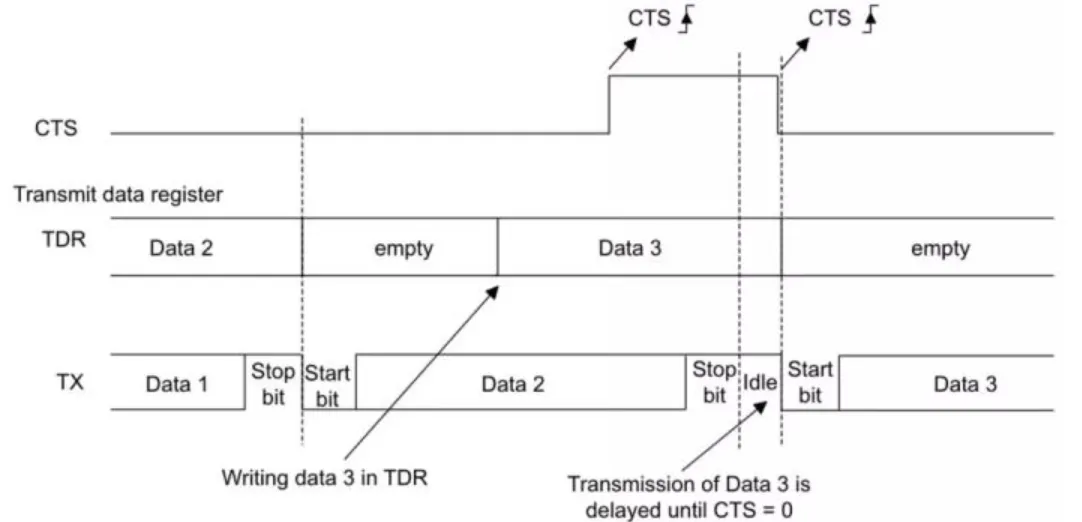
TTL
供电范围在0~5V；>2.7V是高电平；<0.5V是低电平
RS232
±15V
负电平表示逻辑"1"，正电平表示逻辑"0"，通过提高电压差的方式抗干扰
- 负电平范围为-3V至-15V
- 正电平范围为+3V至+15V
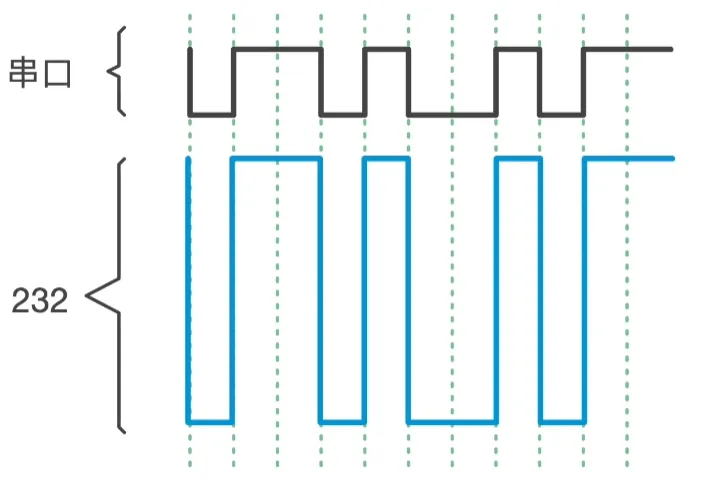
RS485
±6V
通过差分信号抗干扰，当A线高于B线时，表示逻辑"1"；当B线高于A线时，表示逻辑"0"。
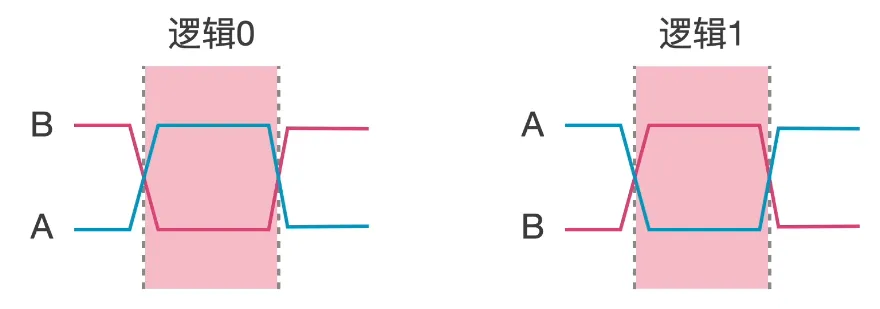
IIC
- 总线空闲时，SCLK与SDA均为高电平
- 连接到总线上的任一器件，输出低电平，都将使总线的信号变低。
- 连接总线的器件输出级必须是集电极或漏极开路，以形成线“与”功能。
- 每个具有IIC接口的设备都有一个唯一的地址，也叫做设备地址，通讯时需要进行寻址。
开始信号：SCL 为高电平时，SDA 由高电平向低电平跳变，开始传送数据。（SDA先拉低）
结束信号：SCL 为高电平时，SDA 由低电平向高电平跳变，结束传送数据。（SCL先拉高）
应答信号：每当主机发送完1Byte，总要等待从机给出1bit的应答信号，以确认从机是否成功接收到了数据（主机SCL拉高，读取从机SDA的低电平为应答）
采样点：稳态电平采样
当SCL=1高电平时进行数据采样，数据线SDA不允许有电平跳变，否则视为开始与停止信号
通信过程：
- 主机发送起始信号
- 主机发送1Byte（从机地址+后续数据传送方向）每个器件具有唯一地址7bit，数据方向：0写1读
- 从机发送应答信号1bit
- 发送方与接收方相继发送1Byte+应答信号
- 主机发送结束信号
写时序
读时序
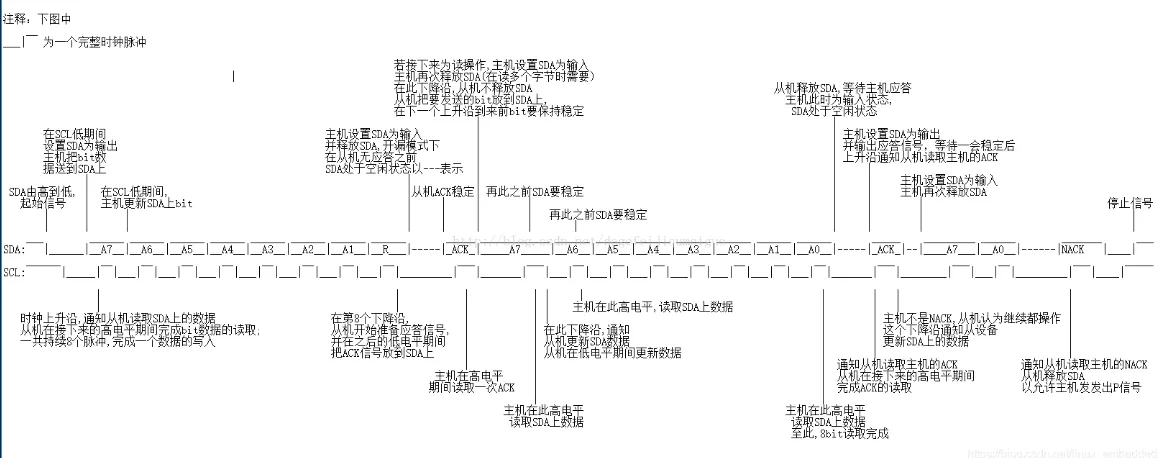
冲突检测与仲裁：（发送方监测，发送电平与SDA电平不符时关闭输出）
-
一种简单的预防冲突机制是：设备在发送数据之前，需要进行冲突检测，检测的依据就是检查SDA的电平状态：只要检测到SDA为低电平，那就是表示总线处于被占用的状态，那么，为了避免发生冲突，当前设备必须等待一段时间以后再次去检测SDA的电平状态，如果总线变成“空闲”的了（即SDA为高电平），那么该设备才能进行通信。
-
这里有一个关键点就是：如何保证连接到I2C总线上的多个的设备，只要存在一个设备占用了总线，其他设备无论如何也不能使总线变为空闲呢？上文说的集电极开路结构就能达到这个要求。
-
每个设备的SDA输出的值，不完全相同，但是，只要有一个为“0”，其结果就是“0”，这就是线与，其可以保证SDA线上的信号，要么稳定为“0”（至少一个设备输出为0），要么稳定为“1”（全部设备输出都为1）。
主机代码
c//总线启动条件
void IIC_Start(void) {
SDA = 1;
SCL = 1;
IIC_Delay(DELAY_TIME);
SDA = 0;
IIC_Delay(DELAY_TIME);
SCL = 0;
}
//总线停止条件
void IIC_Stop(void) {
SDA = 0;
SCL = 1;
IIC_Delay(DELAY_TIME);
SDA = 1;
IIC_Delay(DELAY_TIME);
}
//通过I2C总线发送数据
void IIC_SendByte(unsigned char byt) {
unsigned char i;
for(i=0; i<8; i++)
{
SCL = 0;
IIC_Delay(DELAY_TIME);
if(byt & 0x80)
SDA = 1;
else
SDA = 0;
IIC_Delay(DELAY_TIME);
SCL = 1;
byt <<= 1; //从最高位开始传输数据
IIC_Delay(DELAY_TIME);
}
SCL = 0;
}
//等待应答
bit IIC_WaitAck(void) {
bit ackbit;
SDA = 1; //新加，释放数据总线，若被从机拉低证明ACK数据有效
IIC_Delay(DELAY_TIME);
SCL = 1;
IIC_Delay(DELAY_TIME);
ackbit = SDA;
if(ackbit) //新加，若无应答，则停止总线
IIC_Stop();
SCL = 0;
IIC_Delay(DELAY_TIME);
return ackbit;
}
从机代码
c//从机发送应答
void IIC_SendAck(bit ackbit) {
SCL = 0;
SDA = ackbit; // 0：应答，1：非应答
IIC_Delay(DELAY_TIME);
SCL = 1;
IIC_Delay(DELAY_TIME);
SCL = 0;
SDA = 1;
IIC_Delay(DELAY_TIME);
}
//从I2C总线上接收数据
unsigned char IIC_RecByte(void) {
unsigned char i, da;
for(i=0; i<8; i++)
{
SCL = 1;
IIC_Delay(DELAY_TIME);
da <<= 1; //从高位开始接受数据
if(SDA)
da |= 1;
SCL = 0;
IIC_Delay(DELAY_TIME);
}
return da;
}
IIC从机地址配置方式
-
内部固定地址：某些 I2C 从机设备具有内部固定的从机地址，无法进行配置或更改。在这种情况下，从机地址是设备制造商预定义的。
-
硬件引脚配置：一些 I2C 从机设备具有专用引脚或引脚配置选项，用于设置从机地址。通过使用跳线帽、电阻、芯片的引脚配置等方式，用户可以将特定的引脚配置为高电平或低电平，从而设置从机地址。
-
寄存器配置：一些 I2C 从机设备允许使用特殊的寄存器配置来设置从机地址。这通常通过主机和从机之间的特殊序列和命令来实现。
IIC地址交换
运行过程中，如果新的IIC设备接入，主机和从机如何交换地址？
- 主机发送广播地址（遍历所有预定义的地址进行扫描），等待应答
- 从机监听到自己地址后进行应答
IIC最大设备数量
I2C 协议使用地址来选择特定的从设备进行通信。每个从设备都有一个唯一的 7 位或 10 位地址。
在 I2C 协议中，最多可以有 128 个 7 位地址设备和 1024 个 10 位地址设备。但实际可连接的设备数量受制于总线负载和电气特性等因素。
SPI
四种模式：
时钟极性(CPOL)定义了时钟空闲状态电平：
- CPOL=0，表示当SCLK=0时处于空闲态，所以有效状态就是SCLK处于高电平时
- CPOL=1，表示当SCLK=1时处于空闲态，所以有效状态就是SCLK处于低电平时
时钟相位(CPHA)定义数据的采集时间。
- CPHA=0，在时钟的第一个跳变沿（上升沿或下降沿）进行数据采样。，在第2个边沿发送数据
- CPHA=1，在时钟的第二个跳变沿（上升沿或下降沿）进行数据采样。，在第1个边沿发送数据
| mode | CPOL | CPHA | 描述 |
|---|---|---|---|
| mode 0 | 0 | 0 |  |
| mode 1 | 0 | 1 |  |
| mode 2 | 1 | 0 |  |
| mode 3 | 1 | 1 |  |
一主多从时的连接：（多CS）（菊花链）
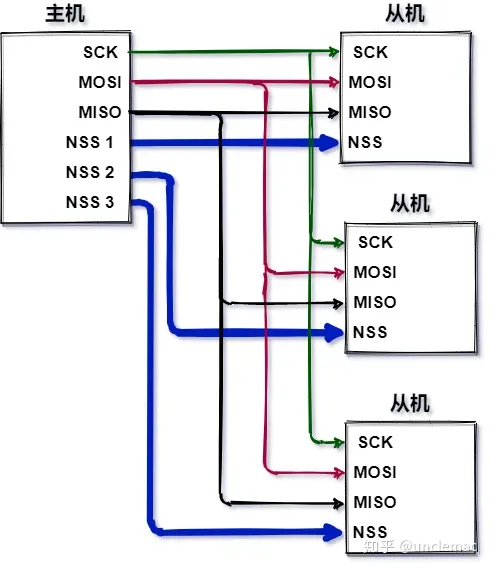
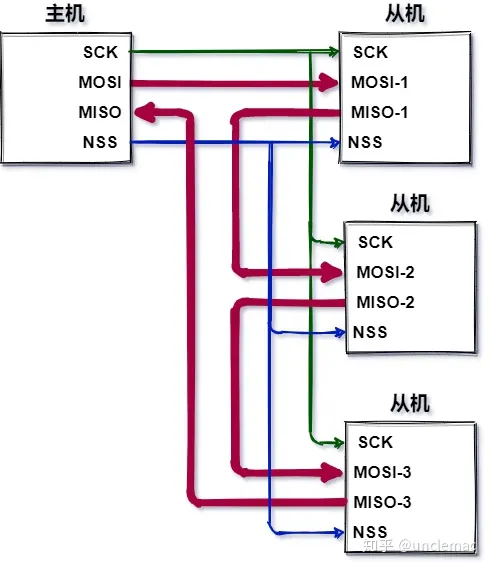
软件SPI与硬件SPI：
- 软件SPI用GPIO口的电平变化模拟SPI通信时序，移植性好，占用CPU资源，速度慢
- 硬件SPI用HAL库封装的HAL_SPI_Transmit即可，占用CPU资源少，速度快，但对PCB走线有要求
采样点：边沿采样
SPI接口的一个缺点：没有指定的流控制，没有应答机制确认是否接收到数据。
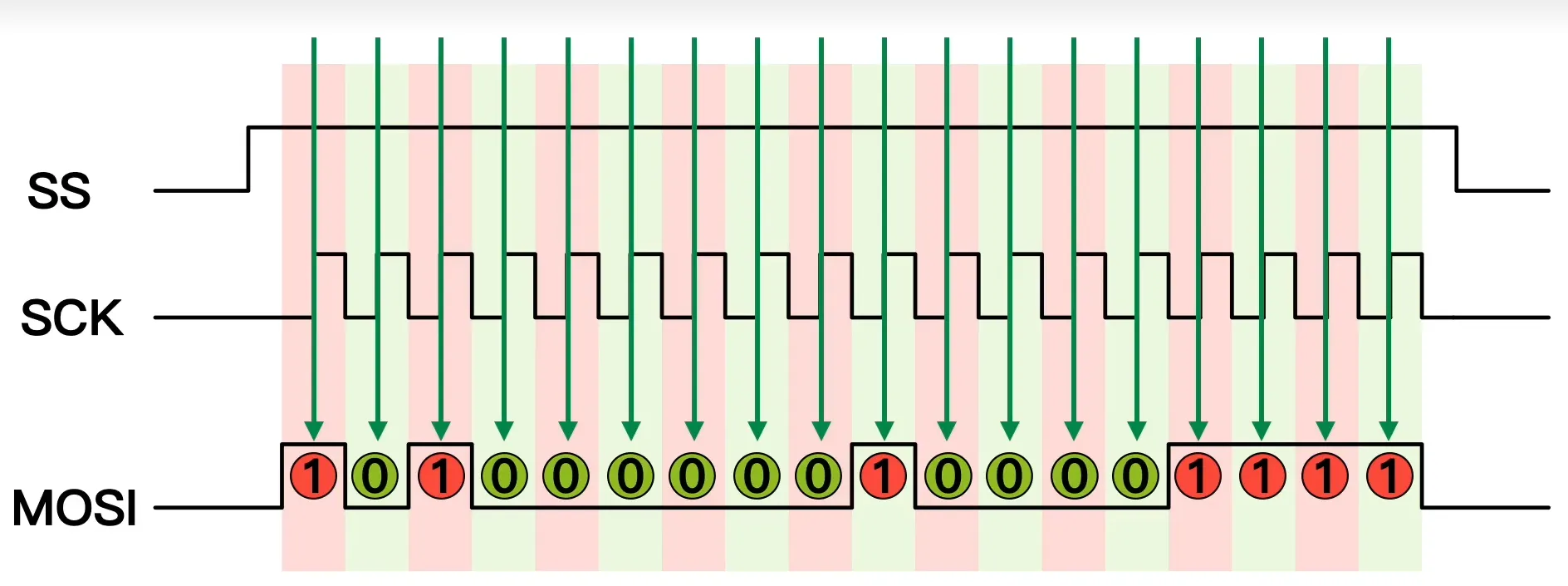
CAN
物理层：两条线差分电平0~5 V，CAN H电压高于CAN L为显性电平（逻辑0），采用CAN收发器将TX RX电平转换为差分，各设备采用ID号区分
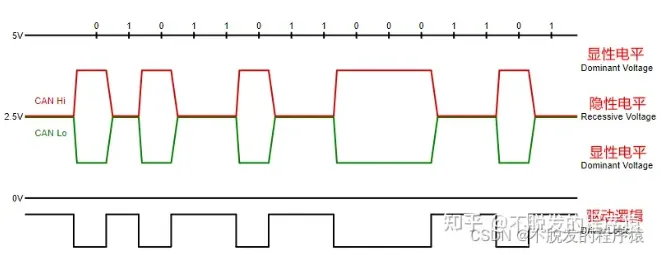
标准： bx CAN 2.0 b： 1 Mbps，每帧8 Byte带CRC
CAN FD： 8 Mbps，每帧64 Byte
时序：保证总线上各设备时钟不同步情况下，通信是同步的，将1 Bit分为三段再分为多个Tq
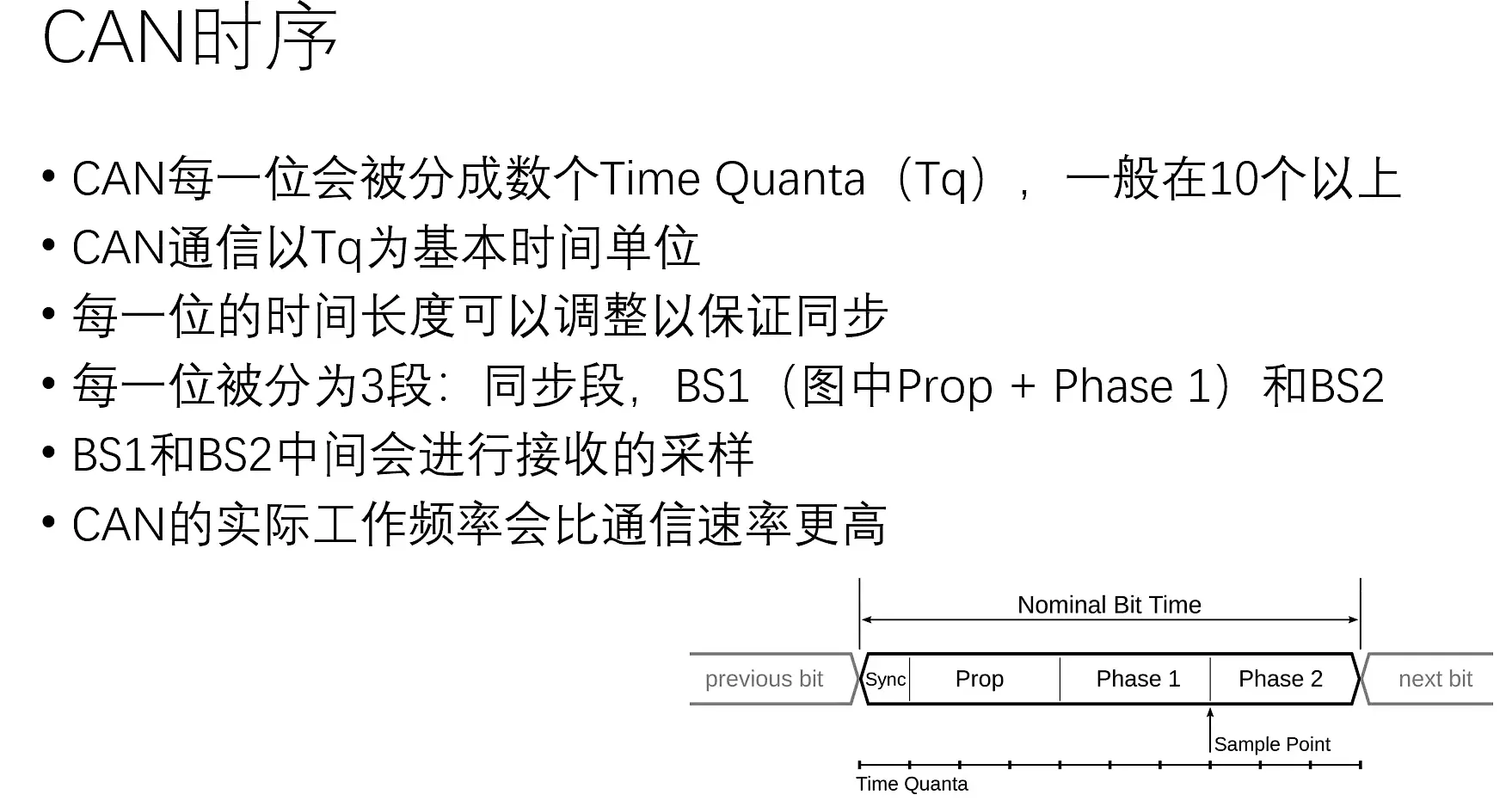
数据帧：存在连续5个以上相同位，帧中需要插入一个相反的位（stuff bit）
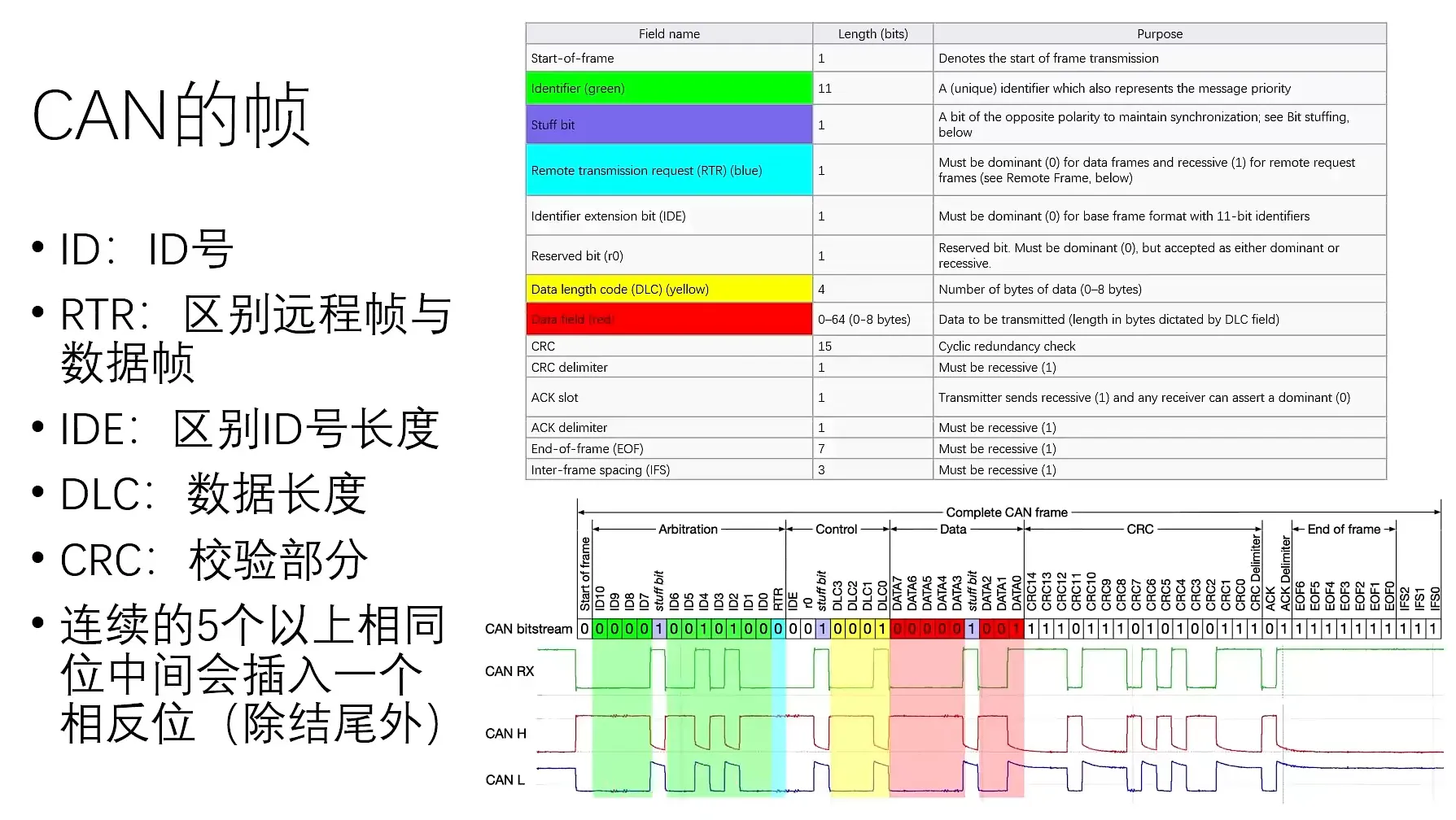
仲裁：CAN 为半双工，不可同时收发，依据ID号中的0的数量进行仲裁
STM32 CAN结构：
过滤器：实际使用中采用列表模式，资源紧张时采用掩码模式
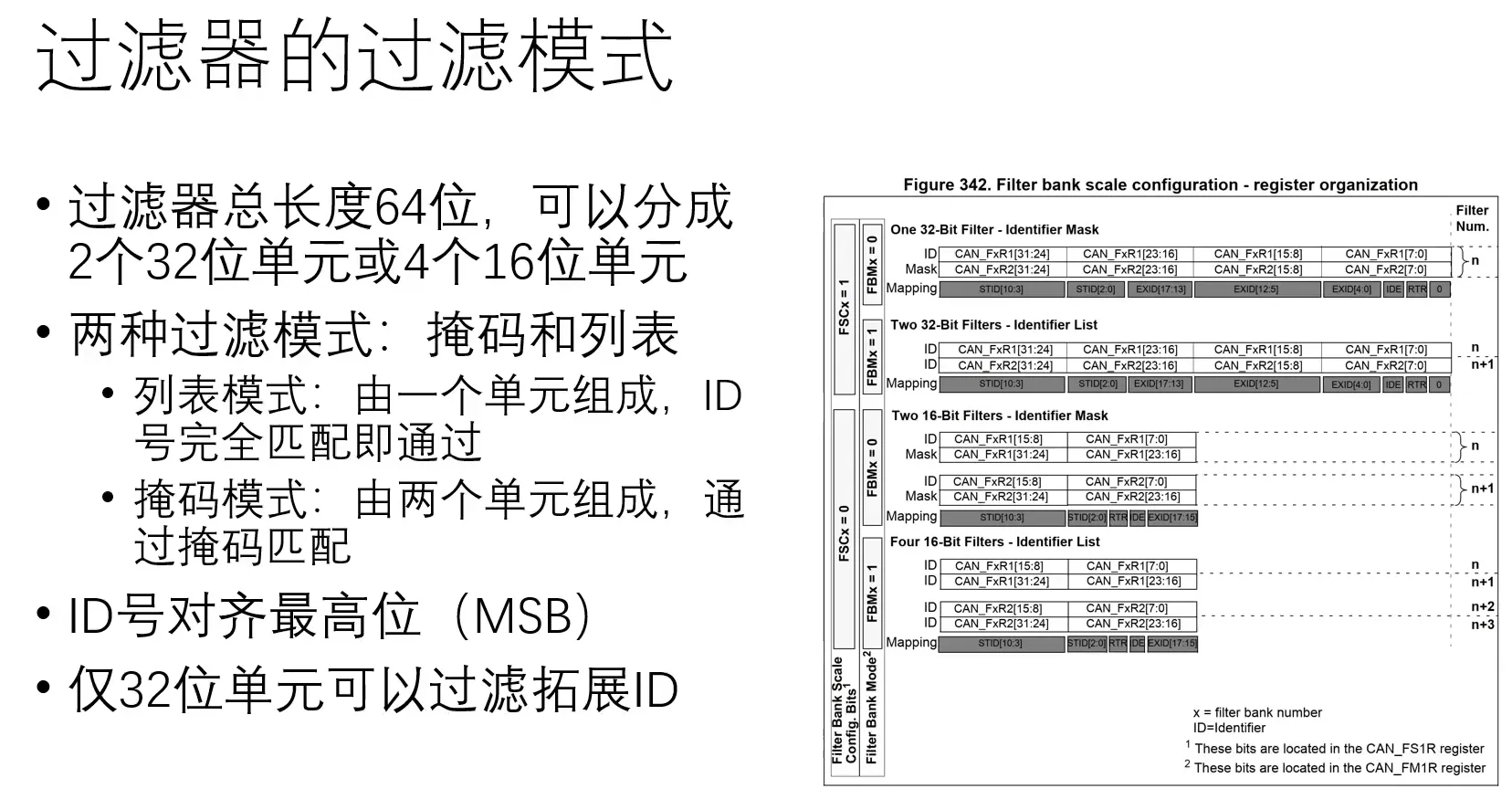
此处有误，应是0x00 0x1FF与0x100掩码，按位与为1的位需要匹配，为0的位不滤除
双接收中断FIFO：
每当收到一个报文，CAN就将这个报文先与FIFO_0关联的过滤器比较，如果被匹配，就将此报文放入FIFO_0中。如果不匹配，再将报文与FIFO_1关联的过滤器比较，如果被匹配，该报文就放入FIFO_1中。如果还是不匹配，此报文就被丢弃
CAN最多可以挂载110个节点，依据总线负载率<70%
内存
内存模型 data bss heap stack
- Flash = Code + RO-data + RW-data
- RAM = RW-data + ZI-data
内存四区：代码区，全局区，堆区，栈区
| 地址 | 区域 | 内容 | 存放位置 | 举例 |
|---|---|---|---|---|
| 0x0000 | .text 代码段 | 编译后的机器码 | Flash | #define ro_def 0x11111111UL |
| .ROdata | 只读常量 | Flash | const uint32_t ro_var = 0x22222222; | |
| .RWdata 已初始化 | 静态变量、全局变量，启动时从Flash读取已初始化数据搬运到RAM | RAM | int global_var= 123; static int c = 0; | |
| .bss 未初始化 | 全局变量，启动时，自动初始化为0 | RAM | int global_var; | |
| .heap 堆 | 动态内存分配，程序员手动开辟释放，向↓增长 | |||
| ---------- | ||||
| 0xFFFF | .stack 栈 | 函数局部变量，由编译器开辟释放，向↑增长 |
初始化过程：数据一开始都存储与ROM中，其中包含RO DATA（常量）、text（代码）、RW DATA（先存储于flash，上电后搬运到RAM）。RAM：加载来自于ROM 的 RW DATA，随后依据启动文件初始化ZI DATA为0
数组下标越界
cint arr[5];
arr[-1]; // 可能可以正常执行
arr[5]; // 一定报错
由于函数栈的增长方向为高地址->低地址，高地址处存放函数返回信息和比数组先存入的信息，并且数组的存储顺序为下标小的元素在低地址，因此往高地址越界时会改写原本栈中的数据，往低地址越界修改的是空的未使用的栈，可能不出问题。
解决方案：利用assert和迭代器来避免
MCU采用 XIP（eXecute In Place）的方式在 Flash 中运行程序，而不是搬运到 RAM 中
- 节省内存空间：MCU 往往具有较小的内存容量，特别是 RAM 的容量较有限。使用 XIP 可以避免将程序复制到 RAM 中造成内存空间的占用，从而节省了宝贵的 RAM 空间，可以将 RAM 用于其他需要快速存取的数据。
- 成本优势：RAM 往往比 Flash 的价格更高，因此将程序直接运行在 Flash 中可以降低系统成本。在 MCU 中，Flash 往往是固化在芯片内部的，而 RAM 需要额外的外部芯片或部件支持，增加了系统的复杂性和成本。
- 提高读取速度：Flash 存储器通常具有较快的访问速度，对于微控制器来说，执行程序时可能已经足够快。在 XIP 模式下，不需要将程序从 Flash 复制到 RAM，节省了在复制过程中的时间，可以直接在 Flash 中运行，加快了程序的启动时间和响应速度。
- 适用于嵌入式系统：MCU 往往嵌入在一些资源受限、功耗要求较低的嵌入式系统中。使用 XIP 可以减少对外部 RAM 的需求，降低功耗，并且提高系统整体的稳定性和可靠性。
尽管 XIP 有以上的优势，它仍然存在一些限制和考虑因素，例如访问延迟较高、不适用于频繁写操作的场景等。因此在设计 MCU 的时候需要综合考虑具体的应用场景和需求来选择合适的存储方案。
Linux栈一般多大
- Linux栈的大小可以在编译内核时进行配置，并且可以根据系统需求进行调整。栈的大小决定了每个线程的可用栈空间大小。
- 在大多数Linux系统上，默认的栈大小为8MB。但是，这个值并不是固定的，可以通过修改内核参数或使用特定的命令来改变栈的大小。
为什么栈从上往下（高地址->低地址）生长？
- 栈的生长方向：指的是入栈方向，从高地址向低地址生长叫做向下生长，或逆向生长。STM32的栈是向下生长
- 当需要分配新的栈帧时，栈指针将向较低的内存地址方向移动，为新的栈帧分配空间。而当不再需要某个栈帧时，栈指针会向较高的内存地址方向移动，释放该栈帧所占用的内存空间。
操作系统对内存管理的作用
- 内存分配与回收
- 采用虚拟内存进行扩容
- 负责逻辑地址到物理地址的转换
- 实现内存保护与隔离（应用间、内核隔离）
分页管理
定义：将内存分为大小相等的页框、进程也分为页框，OS将进程的页框一一对应放入内存
在进程控制块PCB中存放页表，记录了进程页号和内存块号之间的对应关系
逻辑地址到物理地址的转换
- 依据逻辑地址，整除页面大小得到页号，余数为页内偏移量
- 判断越界
- 通过PCB中保存的页表查询该页存放在哪一块内存（逻辑内存地址）
- 通过逻辑内存地址计算实际物理内存地址
缺页中断
为了使得页表不用常驻内存，将页表分为2级管理，1级页表存储页表索引，2级页表存储内存逻辑地址
当某些页面不在内存中但被访问到时发生缺页中断
虚拟内存
将即将使用的数据装入内存，若内存满了，将不用的数据换入磁盘
第一，虚拟内存可以使得进程对运行内存超过物理内存大小，因为程序运行符合局部性原理，CPU 访问内存会有很明显的重复访问的倾向性，对于那些没有被经常使用到的内存，我们可以把它换出到物理内存之外，比如硬盘上的 swap 区域。
第二，由于每个进程都有自己的页表，所以每个进程的虚拟内存空间就是相互独立的。进程也没有办法访问其他进程的页表，所以这些页表是私有的，这就解决了多进程之间地址冲突的问题。 第三，页表里的页表项中除了物理地址之外，还有一些标记属性的比特，比如控制一个页的读写权限，标记该页是否存在等。在内存访问方面，操作系统提供了更好的安全性。
Nor Flash Nand Flash
NoR Flash中不仅可以存储数据，且可以取指运行(XIR)，也就是MCU给出地址，Nor可以直接返回指令交给MCU去执行，这样不用把指令拷贝到RAM里去执行；
NAND Flash仅可用于存储，取值时需要搬运到RAM中
堆和栈的区别
申请方式：stack：系统分配与回收（栈内存分配运算内置于处理器的指令集）；heap：程序员申请与释放
存储位置与方向：stack：高地址—》低地址；heap：低地址—》高地址
碎片问题：stack无碎片FIFO；heap存在内外碎片
存放内容：stack：函数返回地址、局部变量的值；heap：用户定义
栈的动态分配主要是malloc函数实现的，由编译器自动释放；堆只有动态分配用new实现，由程序员手动释放
内存碎片
内存碎片分为内碎片与外碎片
外碎片：还没有被分配出去（不属于任何进程），但由于太小了无法分配给申请内存空间的新进程的内存空闲区域。
内碎片：已经被分配出去（能明确指出属于哪个进程）却不能被利用的内存空间；（按固定大小分配给进程）
产生原因：分配较多不连续的空间后，剩余可用空间被孤立
内存对齐
- 平台原因(移植)：不是所有的硬件平台都能访问任意地址上的任意数据；某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。
- 性能原因：为了访问未对齐的内存，处理器需要作两次内存访问；而对齐的内存访问仅需要一次访问。
如果一个变量的内存地址正好位于它长度的整数倍，他就被称做自然对齐。如果在 32 位的机器下， char 对齐值为1， short 为2， int，float为4，double 为 8
cstruct asd1{
char a;
char b;
short c;
int d;
};//8字节
struct asd2{
char a;
short b;
char c
int d;
};//12字节
规则：按照#pragma pack指定的数值和这个数据成员自身长度中，比较小的那个进行（最后一个char也占用4Byte）
c#pragma pack(4)
struct asd3{
char a;
int b;
short c;
float d;
char e;
};//20字节
#pragma pack()
#pragma pack(1)
struct asd4{
char a;
int b;
short c;
float d;
char e;
};//12字节
#pragma pack()
malloc的底层实现
调用malloc时，去内存空闲链表内寻找可分配的空间，返回首地址指针
以RTT为例：内存管理方法可分为一、内存堆管理（小内存、slab大内存、多内存memheap）与二、内存池管理
一、内存堆管理`
小内存管理：从整块内存中通过链表寻找空闲内存块（逐一向后寻找匹配空间）
slab：将整块内存分为多个不同大小的类别（对号入座）适合于大量的、细小的数据结构的内存申请的情况
memheap：多个地址不连续内存，将其连接起来使用
二、内存池管理
内存池：类似slab，分配大块内存
对比：
| 分配算法 | 优点 | 缺点 | 使用场景 |
|---|---|---|---|
| 内存堆 | 可分配任意大小内存 | 每次均需要查找、容易产生碎片 | 大量细小内存 |
| 内存池 | 分配高效 | 无法分配小内存 | 块设备大量数据 |
虚拟内存
通过地址转换，使得应用程序运行在连续内存上，且与内核隔离
程序的装入、静态链接、动态链接
一、绝对装入（编译时确定绝对地址）
- 再另一台内存不同的电脑上可能无法运行
二、静态重定位（保存相对地址）（读取时转换）
- 编译、链接后存放为逻辑地址，保存的都是相对于0地址的相对值
- 地址空间必须连续且读入内存时，对所有逻辑地址进行运算，转换为物理地址（读入时）
三、动态重定位（保存相对地址）（运行时转换）
- 程序读入内存后，并不直接计算物理地址，实际执行时才进行转换，将逻辑地址转换为物理地址（调用时）
页表
带有权限属性，放在物理内存中的，用来记录虚拟内存页与物理页映射关系的一张表
功能：（虚拟地址与物理地址转换）、（隔离各进程）、（各进程分配连续空间）、（权限管理RW）
| 一级页表 | 多级页表 | 快表 | |
|---|---|---|---|
| 内存访问速度 | 2次（访问页表+访问数据） | 多次（访问一级、二级后访问数据） | 用高速缓存存放常用的页表项 |
| 空间利用率 | 低，虚拟内存越大，页表越大，内存碎片化严重（页表数量限制） | 高，按需分配各级页表 | / |
在1G内存的计算机中能否malloc(1.2G)？
在操作系统上可以，malloc申请的是虚拟内存，而非实际硬件内存。在硬件上不行
brk()与mmap()
在标准C库中，提供了malloc/free函数分配释放内存，这两个函数底层是由brk（C++）sbrk（C），mmap，munmap这些系统调用实现的
进程分配内存的方式有两种系统调用方式：brk与mmap
- brk是将数据段(.data)的最高地址指针_edata往高地址推（高地址释放后低地址才能释放，只适用于小内存分配，碎片多）
- mmap是在进程的虚拟地址空间中（堆和栈中间，称为文件映射区域的地方）找一块空闲的虚拟内存（可以单独释放，碎片少）
相同点：分配的都是虚拟内存，首次访问时发生缺页中断，操作系统再负责分配物理内存，随后建立映射关系
FLEX RAM
TCM : Tightly-Coupled Memory 紧密耦合内存 。ITCM用于指令，DTCM用于数据，特点是跟内核速度一样（400MHz），而片上RAM的速度基本都达不到这个速度（200MHz）。很多时候我们希望将需要实时性的程序和变量分别放在ITCM和DTCM里面执行，本章就是解决这个问题。
- ITCM（指令紧耦合存储器）：
- ITCM用于存储指令（程序代码），通常具有较低的访问延迟和较高的带宽，以提供快速和可预测的指令访问。
- ITCM通常与处理器核心直接相连，使得指令可以快速地从该存储区加载，从而加快指令执行速度。
- ITCM的容量相对较小，通常只能存储少量的指令代码。
- DTCM（数据紧耦合存储器）：
- DTCM用于存储数据，如变量、栈、堆等，具有较低的读写访问延迟和高带宽。
- DTCM与处理器核心直接相连，以提供快速的数据访问，使得数据可以快速加载和存储，提高数据操作的效率。
- DTCM的容量通常相对较小，只能存储有限量的数据。
- OCRAM（片上随机访问存储器）：
- OCRAM是一种通用的片上随机访问存储器，用于存储数据和指令。
- OCRAM的容量通常比ITCM和DTCM更大，可以存储更多的数据和代码。
- OCRAM的访问速度和带宽一般较低，但相对来说会比外部存储器的访问速度快。
三者之间的主要区别在于其设计目标和功能。ITCM主要用于存储指令代码，提供快速指令访问；DTCM主要用于存储数据，提供快速数据访问；OCRAM则是一种通用存储器，可以同时存储指令和数据，容量相对较大，但速度和带宽可能不如ITCM和DTCM。
大家都知道 RAM 是掉电易失的，这种加速的方法如何在量产产品中使用呢？实际上使用以上的方法，MDK 会将特定的函数编译到 ROM 当中，在每次启动的时候都会将 ROM 中指定的函数拷贝到 RAM 放中。
【经验分享】STM32H7时间关键代码在ITCM执行的超简单方法 (stmicroelectronics.cn)
STM32
STM32启动流程
1.依据boot引脚选择启动区域
| 引脚 | 启动方式 | 描述 |
|---|---|---|
| x 0 | 片内Flash | 代码区启动，ICP下载（SWD、JTAG烧录） |
| 0 1 | 系统存储器 | 内置ROM启动，ISP下载（出厂预置代码，UART烧录） |
| 1 1 | SRAM | RAM启动，掉电丢失 |
2.运行bootloader
处理器会将各个寄存器的值初始化为默认值
2.1 硬件设置SP、PC，进入复位中断函数Rest_Hander()
从0x0800 0000读取数据赋值给栈指针SP(MSP)，设置为栈顶指针0x2000 0000+RAM_Size
从0x0800 0004读取数据赋值给PC（指向Reset_Handler中断服务函数）
cLDR R0, = SystemInit BLX R0
2.2 设置系统时钟，进入SystemInit()
设置RCC寄存器各位
设置中断向量表偏移地址
c#ifdef VECT_TAB_SRAM
SCB->VTOR = SRAM_BASE | VECT_TAB_OFFSET; /* Vector Table Relocation in Internal SRAM. */
#else
SCB->VTOR = FLASH_BASE | VECT_TAB_OFFSET; /* Vector Table Relocation in Internal FLASH. */
#endif
2.3 软件设置SP，__main入栈（统初始化函数）
cLDR R0,=__main BX R0
2.4 加载data、bss段并初始化_main栈区
拷贝Flash中的数据进入SRAM（哈弗体系结构决定了：数据与代码分开存储）
3 跳转到main()
OTA的情况
在FLASH中添加引导程序后，其与APP程序将各自对应一个中断向量表，假设引导程序占用N+M Byte的FLASH空间。上电后，单片机从复位中断向量表处获取地址，并跳转执行复位中断服务函数，执行完毕后执行主函数，随后执行Bootloader中程序跳转的相关代码跳转至APP，即地址0x08000004+N+M处。进入主函数的步骤与Bootloader函数一致。当运行在主函数时，若有中断请求被响应，此时PC指针本应当指向位于地址0x08000004处的中断向量表，但由于程序预先通过“SCB->VTOR = 0x08000000 | ADDR_OFF;”这一语句，使得中断向量表偏移ADDR_OFF（N+M）地址，因此PC指针会跳转到0x08000004+N+M处所存放的中断向量表处，随后执行本应执行的中断服务函数，在跳出函数后再进入主函数运行。
cvoid iapLoadApp(uint32_t appxAddr)
{
iapfun jumptoapp;
if( 0x20000000 == ( (*(vu32*)appxAddr) & 0x2FFE0000) )//检查appxaddr处存放的数据(栈顶地址0x2000****)是不是在RAM的地址范围内
{
jumptoapp = (iapfun)*(vu32*)(appxAddr + 4);//拷贝APP程序的复位中断函数地址，用户代码区第二个字为程序开始地址(复位地址)（强制跳转到函数地址处执行，函数指针的方式）
MSR_MSP(*(vu32*)appxAddr);//初始化APP堆栈指针(用户代码区的第一个字用于存放栈顶地址)，重新分配RAM
jumptoapp();//执行APP的复位中断函数，跳转到APP
}
}
中断的过程
中断初始化
-
设置中断源，让某个外设可以产生中断；
-
设置中断控制器，使能/屏蔽某个外设的中断通道，设置中断优先级等；
-
使能CPU中断总开关
CPU在运行正常的程序
产生中断，比如用户按下了按键 —> 中断控制器 —> CPU
CPU每执行完一条指令（指令有多个时钟周期，取指、译码、执行等）都会检查是否有异常/中断产生
发现有异常/中断产生，开始处理：
-
保存现场（PC、LR、MSP、通用寄存器、FPU压栈）
-
分辨异常/中断，调用对应的异常/中断处理函数
-
恢复现场（PC与出栈）
在执行高优先级中断时如果低优先级中断到来，低优先级中断不会被丢失
当中断发生时，PC设置为一个特定地址，这一地址按优先级排列就称为异常向量表
STM32定时器
系统滴答定时器SysTick（并非外设，CM3内核）
看门狗定时器WatchDog
基本定时器TIM6,TIM7
通用定时器TIM2,TIM3,TIM4,TIM5（输出比较、输入捕获、PWM、单脉冲）
高级定时器TIM1,TIM8（死区控制）
基本定时：预分频、重装载寄存器
PWM：预分频、重装载、比较寄存器
STM32 ADC
STM32F1 ADC，精度为12位，每个ADC最多有16个外部通道，各通道的A/D转换可以单次、连续扫描或间断执行，ADC转换的结果（6-12位）可以左对齐或右对齐储存在16位数据寄存器中。ADC的输入时钟不得超过14MHz，其时钟频率由PCLK2分频产生。
一个ADC的不同通道读取的值在共用的DR寄存器中，进行下一个通道采集前需要将数据取走否则丢失
注入通道：可以在规则通道转换时，强行插入转换
参考电压：3.3V
采集精度与位数：最大测量电压/2^采样位数，例如3.3V / 2^12，采样逐次逼近
精度
实际值和采样值的偏差
分辨率
10cm长的尺子，最小刻度是1mm，分辨率是1mm
由采样位数决定。一个12位的ADC可以将输入电压转换为4096个离散的数值（2^12 = 4096）
STM32 DMA
当外部设备（如硬盘、显卡、网络适配器等）需要与主存储器进行数据交换时，需要通过中央处理器（CPU）作为中介来完成数据传输操作。然而，在大量数据传输的情况下，这样的方式会造成CPU过多地参与数据传输，降低了整体性能。
CPU将外设数据搬运到内存的顺序：
- 外设设置状态寄存器置位
- CPU读取外设数据寄存器到CPU通用寄存器
- CPU将通用寄存器数据写入内存
CPU不介入情况下，将数据在外设与内存中传递
DMA配置：数据宽度（u8 u16 u32），数据量(sizeof)，数据地址
循环模式：单轮传输结束后，重置传输计数器，重置传输地址为初始值，再次开始新一轮循环
双缓冲区：一个缓冲区传输完成中断触发后，缓存地址乒乓交换，同时触发回调函数
DMA会节约总线资源吗（不能，他只是节约了CPU）
DMA配置
- 配置DMA控制器：设置DMA通道、数据传输方向（外设到存储器或存储器到外设）、传输模式（单次传输、循环传输等）、数据宽度、传输计数等参数
- 分配内存：如果是外设到存储器的数据传输，需要分配一块足够大小的缓冲区
- 配置DMA通道：将外设和DMA通道连接起来，通常需要配置外设的DMA请求触发方式和DMA通道的优先级等参数。
- 触发DMA传输：启动数据的传输。DMA控制器将自动执行数据的传输，而不需要CPU的干预。
实际应用
- 分析性能瓶颈在哪，是数据频率还是数据量过大
- 数据频率：双DMA BUF
- 数据量：单个大 DMA BUF
STM32中断
定义：正在执行某事件时，被某事件打断，造成任务切换
分类：内核异常、外部中断
嵌套向量中断控制器NVIC：多个优先级中断到来后的处理顺序
处理流程：CPU收到(interrupt request，IRQ)后，通过上下文切换保存当前工作状态，跳转至中断处理函数执行（中断向量表），完成后再出栈执行原有程序
中断和异常
相同点：都是CPU对系统发生的某个事情做出的一种反应
区别：中断由外因引起，异常由CPU本身原因引起
STM32看门狗
定时喂狗，否则触发系统复位
IWDG独立看门狗：采用独立时钟，监视硬件错误
WWDG窗口看门狗：采用系统时钟，监视软件错误（必须在规定时间窗口刷新）（防止跑飞后跳过某些代码段）（进入WWDG中断时，可以保存复位前的数据）
IO口类型
| 分类 | 电平 | 用途 | 备注 |
|---|---|---|---|
| 上拉输入 | 常态高电平（上拉电阻连接VCC） | IO读取 | |
| 下拉输入 | 常态低电平（下拉电阻连接GND） | IO读取 | |
| 推挽输出 | 可以输出高电平和低电平，都有较强驱动能力，IO输出0-接GND， IO输出1 -接VCC | 一般IO输出 | 驱动负载能力强 |
| 开漏输出 | 只能输出低电平，高电平没有驱动能力，需要外部上拉电阻才能真正输出高电平 | 线与功能 | 像IIC中，只要有一个给低电平，那么总线都会被拉低。实现线与功能 |
STM32 主频、Flash、SRAM大小
| 类型 | 主频 | Flash | RAM | 内核 |
|---|---|---|---|---|
| STM32F407IGH6 | 168M | 1024KB | 192KB | M4 |
| STM32L151RET6 | 32M | 512KB | 80KB | M3 |
| STM32F103C8T6 | 72M | 64KB | 20KB | M3 |
| HC32L130E8PA | 48M | 64KB | 8KB | M0+ |
ADC采样原理
逐次逼近转换过程和用天平称物重非常相似。天平称重物过程是，从最重的砝码开始试放，与被称物体进行比较，若物体重于砝码，则该砝码保留，否则移去。再加上第二个次重砝码，由物体的重量是否大于砝码的重量决定第二个砝码是留下还是移去。照此一直加到最小一个砝码为止。将所有留下的砝码重量相加，就得此物体的重量。仿照这一思路，逐次比较型A/D转换器，就是将输入模拟信号与不同的参考电压作多次比较，使转换所得的数字量在数值上逐次逼近输入模拟量对应值。
ARM 汇编
assemblyLDR #从存储器中将一个32位的字数据传送到目的寄存器中。该指令通常用于从存储器中读取32位的字数据到通用寄存器，然后对数据进行处理。 LDR R0,[R1] # 将存储器地址为R1的字数据读入寄存器R0 LDR R0,[R1, #8] // 将存储器地址为R1+8的字数据读入寄存器R0 LDR R1, [R0,#0x12] # 将R0+0x12 地址处的数据读出，保存到R1中(R0 的值不变) LDR R1, [R0,R2] # 将R0+R2 地址的数据计读出，保存到R1中(R0 的值不变)
assemblySTR #从源寄存器中将一个32位的字数据传送到存储器中，使用方式可参考指令LDR STR R0,[R1] # 将R0寄存器的数据写入R1地址的内存 STR R0,[R1, #8] # 将R0中的字数据写入以R1＋8为地址的存储器中 STR R0,[R1],#8 # 将R0中的字数据写入以R1为地址的存储器中，并将新地址R1＋8写入R1
assemblyMOV R1 #0x10 ; # R1=0x10 将数值放入R1 MOV R0, R1 ; # R0=R1 将寄存器值放入R1 MOVS R3, R1, LSL #2 ; R3=R1＜＜2，并影响标志位
编译&调试
GCC编译4个过程
- 预处理：展开宏定义，文件嵌套、删除注释
- 编译：转换为汇编（检查语法不检查逻辑）
- 汇编：转换为机器码
- 链接：符号表查找与填充地址，库的链接，将汇编文件中函数的临时0地址进行填充，将每个符号定义与一个内存位置相关联起来
一个程序从开始运行到结束的完整过程（四个过程）
编译预处理、编译、汇编、链接
预处理：（头文件、宏展开、注释去除）gcc -E main.c -o main.i
编译：（语法分析，生成汇编代码）gcc -S main.i -o main.s
汇编：（生成二进制机器码）as main.s -o main.o
链接：（指定路径下寻找库函数）gcc main.o -o main
编译优化选项 -o
| 编译速度 | 代码大小 | 重点 | ||
|---|---|---|---|---|
| o1 | 不变 | 大 | ||
| o2 | 牺牲 | 中 | ||
| o3 | 牺牲 | 中 | 提高速度 | |
| os | 牺牲 | 小 | 降低代码大小 | |
| og | 优化调试体验 |
STM32编译后程序大小与存放位置
1）Code：代码段，存放程序的代码部分；
2）RO-data：(Read Only )只读数据段，存放程序中定义的常量；
3）RW-data：(Read Write)读写数据段，存放初始化为非 0 值的全局变量；
4）ZI-data： (Zero Init) 数据段，存放未初始化的全局变量及初始化为 0 的变量；
cTotal RO Size (Code + RO Data) 53668 ( 52.41kB)
Total RW Size (RW Data + ZI Data) 2728 ( 2.66kB)
Total ROM Size (Code + RO Data + RW Data) 53780 ( 52.52kB)
1）RO Size 包含了 Code 及 RO-data，表示程序占用 Flash 空间的大小；
2）RW Size 包含了 RW-data 及 ZI-data，表示运行时占用的 RAM 的大小；
3）ROM Size 包含了 Code、RO-data 以及 RW-data，表示烧写程序所占用的 Flash 空间的大小；
程序运行之前，需要有文件实体被烧录到 STM32 的 Flash 中，一般是 bin 或者 hex 文件，该被烧录文件称为可执行映像文件。如下图左边部分所示，是可执行映像文件烧录到 STM32 后的内存分布，它包含 RO 段和 RW 段两个部分：其中 RO 段中保存了 Code、RO-data 的数据，RW 段保存了 RW-data 的数据，由于 ZI-data 都是 0，所以未包含在映像文件中。
STM32 在上电启动之后默认从 Flash 启动，启动之后会将 RW 段中的 RW-data（初始化的全局变量）搬运到 RAM 中，但不会搬运 RO 段，即 CPU 的执行代码从 Flash 中读取，另外根据编译器给出的 ZI 地址和大小分配出 ZI 段，并将这块 RAM 区域清零。
编译过程：.c中的变量不分配地址（.o中函数、变量地址为0），链接时依据link file规则分配
链接：将各个.o中的相同段进行合并（.text、.data、.bss），并找到所有符号的引用与定义的位置
交叉编译
定义：在一种环境下，编译另一种环境下运行的代码
是否遇到了系统稳定性问题
用了指针与结构体，为了实现类似C++的特性，存在野指针问题，定位方式：ozone工具debug
依据寄存器PC指针定位到出问题的代码位置，反推函数调用栈，手动查找，并未使用自动化工具分析
控制算法
PID
P：误差*Kp**【弹簧】**
I：误差*Ki后累计**【积分】**
D：当前和之前两次误差的差值*Kd（当过冲时方向相反，为负反馈阻尼）【阻尼】
串级PID
实际使用中由于电流环控制已经由电机实现，因此用户仅实现位置环和速度环
采用串级PID的优势与原因
【1不同工况适应性】对于不同的系统工况，由于电机实际输入是电流（直接控制转速），当电机负载不同时（原有PID参数用于平地行驶，现在爬坡行驶），电机系统模型也不同，采用同一套位置环PID算法较难获得稳定的电机电流输出信号，导致同一套参数的控制效果在其他工况变差。串级PID的引入，使得内环可以让电机速度更快地跟随。
【2系统稳态要求】若仅有位置环PID，达到指定位置时，由于没有对速度的限制，因此可能发生震荡。引入内环后速度也有PID控制器进行反馈，当位置较小时，内环的输入也会变小，从而约束稳态速度减小到0
【3限制速度】对于内环而言，可以采用输出限幅的方式限制转速，从而避免了单位置环PID在偏差较大时电机速度过快。
串级PID的参数整定基本遵循从内到外，先整定内环PID的参数，再整定外环PID的参数
ctypedef struct {
uint8_t mode;
//PID 三参数
fp32 Kp;
fp32 Ki;
fp32 Kd;
fp32 max_out; // 最大输出
fp32 max_iout; // 最大积分输出
fp32 set;
fp32 fdb;
fp32 out;
fp32 Pout;
fp32 Iout;
fp32 Dout;
fp32 Dbuf[3]; // 微分项 0最新 1上一次 2上上次
fp32 error[3]; // 误差项 0最新 1上一次 2上上次
} PID_t;
fp32 PID_Calc(PID_t *pid, fp32 fdb, fp32 set) {
if (pid == NULL) {
return 0.0f;
}
pid->error[2] = pid->error[1];
pid->error[1] = pid->error[0];
pid->set = set;
pid->fdb = fdb;
pid->error[0] = set - fdb;
if (pid->mode == PID_POSITION) {
pid->Pout = pid->Kp * pid->error[0];
pid->Iout += pid->Ki * pid->error[0];
pid->Dbuf[2] = pid->Dbuf[1];
pid->Dbuf[1] = pid->Dbuf[0];
pid->Dbuf[0] = (pid->error[0] - pid->error[1]);
pid->Dout = pid->Kd * pid->Dbuf[0];
LimitMax(pid->Iout, pid->max_iout);
pid->out = pid->Pout + pid->Iout + pid->Dout;
LimitMax(pid->out, pid->max_out);
}
else if (pid->mode == PID_DELTA) {
pid->Pout = pid->Kp * (pid->error[0] - pid->error[1]);
pid->Iout = pid->Ki * pid->error[0];
pid->Dbuf[2] = pid->Dbuf[1];
pid->Dbuf[1] = pid->Dbuf[0];
pid->Dbuf[0] = (pid->error[0] - 2.0f * pid->error[1] + pid->error[2]);
pid->Dout = pid->Kd * pid->Dbuf[0];
pid->out += pid->Pout + pid->Iout + pid->Dout;
LimitMax(pid->out, pid->max_out);
}
return pid->out;
}
KF、EKF、UKF
KF能够使用的前提就是所处理的状态是满足高斯分布的，为了解决这个问题，EKF是寻找一个线性函数来近似这个非线性函数，而UKF就是去找一个与真实分布近似的高斯分布。
KF：最早提出的卡尔曼滤波算法，适用于线性系统，且系统状态和观测误差服从高斯分布。KF通过预测和更新步骤来估计系统的状态，并通过协方差矩阵来描述状态估计的不确定性。然而，KF不能很好地处理非线性系统。
EKF：扩展卡尔曼将非线性系统离散化线性化，并利用线性系统的KF进行状态估差，当非线性度较高时，EKF的估计精度可能下降。
UKF：无迹卡尔曼滤波用来解决非线性系统的问题。UKF通过选取一组称为Sigma点的采样点，保留系统的一阶矩和二阶矩，而不是线性化处理。通过这种方式，UKF能够更好地逼近非线性系统的真实分布，并提供更准确的状态估高斯系统，
卡尔曼滤波
用于过滤高斯噪声（白噪声）
通过k-1时刻的最优估计值预测k时刻的理论值，并根据k时刻的测量值，进行数据融合，得到k时刻的最优估计值（线性离散时不变系统，误差正态分布）
cx(k) = A · x(k-1) + B · u(k) + w(k) // 预测方程：依据k-1时刻的状态，推算k时刻的状态
z(k) = H · x(k) + y(k) // 观测方程
x(k) —— k时刻系统的状态
u(k) —— 控制量
w(k) —— 符合高斯分布的过程噪声，其协方差在下文中为Q
z(k) —— k时刻系统的观测值
y(k) —— 符合高斯分布的测量噪声，其协方差在下文中为R
A、B、H —— 系统参数，多输入多输出时为矩阵，单输入单输出时就是几个常数
在后面滤波器的方程中我们将不会再直接面对两个噪声w(k)和y(k)，而是用到他们的协方差Q和R。至此，A、B、H、Q、R这几个参数都由被观测的系统本身和测量过程中的噪声确定了。
c// 时间更新（预测）
x(k|k-1) = A · x(k-1|k-1) + B · u(k) // 系统状态(x)
P(k|k-1) = A · P(k-1|k-1) · AT + Q // 系统协方差(P)
K(k) = P(k|k-1) · HT · (H · P(k|k-1) · HT + R)-1 // 卡尔曼增益K(k)
// 测量更新（校正融合）
x(k|k) = x(k|k-1) + K(k) · (z(k) - H · x(k|k-1)) // 输出值（后验估计）x(k|k)
P(k|k) = (I - K(k) · H) · P(k|k-1) // 更新误差协方差
实际使用：
cx // 观测量初始值
P // 系统协方差
K // 卡尔曼增益，自动计算
Q // 过程噪声的协方差，对初值不敏感，很快收敛
R // 测量噪声的协方差，↑后平滑但是响应变差且收敛慢
while(新观测值)
{
K = P / (P + R); // 增益
x = x + K * (新观测值 - x); // 输出
P = (1 - K) · P + Q; // 更新
}
float Kalman_Filter(float data) {
static float prevData = 0;
static float p = 1; // 估计协方差
static float q = 1; // 过程噪声协方差
static float r = 5; // 观测噪声协方差，控制响应速率
static float kGain = 0;
p += q;
kGain = p / (p + r); //计算卡尔曼增益
data = prevData + (kGain * (data - prevData)); //计算本次滤波估计值
p = (1 - kGain) * p; //更新测量方差
prevData = data;
return data;
}
c//1. 结构体类型定义
typedef struct {
float LastP;//上次估算协方差 初始化值为0.02
float Now_P;//当前估算协方差 初始化值为0
float out;//卡尔曼滤波器输出 初始化值为0
float Kg;//卡尔曼增益 初始化值为0
float Q;//过程噪声协方差 初始化值为0.001
float R;//观测噪声协方差 初始化值为0.543
}KFP；//Kalman Filter parameter
//2. 以高度为例 定义卡尔曼结构体并初始化参数
KFP KFP_height={0.02,0,0,0,0.001,0.543};
/*卡尔曼滤波器
*@param KFP *kfp 卡尔曼结构体参数
* float input 需要滤波的参数的测量值（即传感器的采集值）
*@return 滤波后的参数（最优值）*/
float kalmanFilter(KFP *kfp,float input) {
//预测协方差方程：k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
kfp->Now_P = kfp->LastP + kfp->Q;
//卡尔曼增益方程：卡尔曼增益 = k时刻系统估算协方差 / （k时刻系统估算协方差 + 观测噪声协方差）
kfp->Kg = kfp->Now_P / (kfp->NOw_P + kfp->R);
//更新最优值方程：k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * （测量值 - 状态变量的预测值）
kfp->out = kfp->out + kfp->Kg * (input -kfp->out);//因为这一次的预测值就是上一次的输出值
//更新协方差方程: 本次的系统协方差付给 kfp->LastP 为下一次运算准备。
kfp->LastP = (1-kfp->Kg) * kfp->Now_P;
return kfp->out；
}
//调用卡尔曼滤波器 实践
float height;
float kalman_height = 0;
kalman_height = kalmanFilter(&KFP_height, height);
C++
面向对象
区别于传统的面向流程，需要抽象出一个类来封装各类方法
- 封装
- 将对象的属性（成员变量）和方法（成员函数）封装到一个类里面，便于管理的同时也提高了代码的复用性。
- 继承
- 最大程度保留类和类之间的关系，提高代码复用性，降低代码维护成本。
- 多态
- 静态多态：编译时确定，函数重载
- 动态多态：运行时确定调用成员函数的时候，会更具调用方法的对象的类型来执行不同的函数。父类指针调用子类对象
继承
public protected peivate
类实例（即类对象）不能直接访问类的 private成员和protected成员，但是能直接访问类的public成员。
无论哪种继承方式，子类都不能直接访问父类的 private成员；但是能直接访问父类的 protected成员和public成员（注意：是子类，而不是类实例），并且能通过父类的protected成员函数和public成员函数间接访问父类的private成员。
对于这三种方式继承的 派生类 来说: 都能访问基类的public, protected 成员;
-
public 的方式继承到派生类，这些成员的权限和在基类里的权限保持一致;
-
protected方式继承到派生类，成员的权限都变为protected;
-
private 方式继承到派生类，成员的权限都变为private;
3.子类通过public方式继承父类，则父类中的public、protected和private属性的成员在 子类 中 依次 是 public、protected和private属性，即通过public继承并不会改变父类原来的数据属性。
4.子类通过protected方式继承父类，则父类中的public、protected和private属性的成员在 子类 中 依次 是 protected、protected和private属性，即通过protected继承原来父类中public属性降级为子类中的protected属性，其余父类属性在子类中不变。
5.子类通过private方式继承父类，则父类中的public、protected和private属性的成员在 子类 中 依次 是 private、private和private属性，即通过private继承原来父类中public属性降级为子类中的private属性，protected属性降级为子类中的private属性，其余父类属性在子类中不变。
注意: 其实父类的原属性并未改变，只是通过 继承关系被继承到子类中的父类成员的个别属性有所变化 ，即只是在子类中父类的个别成员属性降级了，原来父类的成员属性并未变。
友元函数 friend
类的友元函数是定义在类外部，但有权访问类的所有私有（private）成员和保护（protected）成员。尽管友元函数的原型有在类的定义中出现过，但是友元函数并不是成员函数。
c++class Box
{
private:
double width;
public:
friend void printWidth( Box box );
void setWidth( double wid );
};
// 成员函数定义
void Box::setWidth( double wid ) {
width = wid;
}
// 请注意：printWidth() 不是任何类的成员函数
void printWidth( Box box ) {
/* 因为 printWidth() 是 Box 的友元，它可以直接访问该类的任何成员 */
cout << "Width of box : " << box.width <<endl;
}
// 程序的主函数
int main( ) {
Box box;
// 使用成员函数设置宽度
box.setWidth(10.0);
// 使用友元函数输出宽度
printWidth( box );
return 0;
}
static作用，与c的区别
static 作用主要影响着变量或函数的生命周期，作用域，以及存储位置。
一、修饰局部变量：（函数内部、{}内部）
- 变量的存储区域由栈变为静态区。
- 变量的生命周期由局部变为全局。
- 变量的作用域不变。
二、修饰模块内的全局变量：（静态全局变量）
- 变量的存储区域在全局数据区的静态区。
- 变量的作用域由整个程序变为当前文件。（extern声明也不行）（全局变量不暴露）
- 变量的生命周期不变。
三、修饰函数：（当前文件中的函数）
- 函数的作用域由整个程序变为当前文件。（extern声明也不行）（接口不暴露）
四、修饰C++ 成员变量
- 在类外定义与初始化
int A::_count = 0;，类内申明static int _count; - 为该类所有对象所共享
- 访问：类名::变量名
五、修饰C++ 成员函数
- 没有隐藏的
this指针，不能访问非静态成员（变量、 函数） - 不能调用非静态成员函数
- 非静态成员函数可以调用静态成员函数
指针与引用的区别
-
指针：指向一个对象后，对它所指向的变量，间接操作
-
引用：目标变量的别名，直接操作
c++int a = 996;
int *p = &a; // p是指针, &在此是求地址运算
int &r = a; // r是引用, &在此起标识作用
-
引用必须初始化，指针不用
-
引用初始化后不能修改，指针可以改变所指对象
-
指针++为地址，引用++为值
-
sizeof 指针为指针大小，sizeof 引用为数据大小
-
指针转换为引用：*p，随后当参数传入即可
-
引用转换为指针：引用对象&取地址即可
左值引用、右值引用
-
左值是指表达式后可以获取地址的对象。换句话说，左值代表一个可以放在等号左边的值，也可以被修改例如，变量、数组元素和通过引用或指针访问的对象都是左值。 int a = 10; // 其中 a 就是左值
-
右值是指表达式后不可以获取地址的临时对象或字面量。右值代表一个临时值，它只能放在等号右边，不能被修改。例如，数字常量、字符串常量、临时变量、返回的临时对象都属于右值。 int a = 10; // 其中 10 就是右值右值
C++11引入了右值引用（rvalue reference）的概念，允许程序员更方便地对右值进行操作和移动语义，例如移动语义的实现和完美转发。右值引用通过&&表示。
c++int&& r = 42; // 创建一个右引用
移动语义与完美转发 moce fowrard
- std::move是一个函数模板，用于将给定的对象表示为右值（或将其转换为右值用它执行的操作是对传入的对象进行强制转换，使其能够被移动而不是复制。通过使用std::move，我们可以显式地表达出我们要对对象进行移动操作，以便在适当的情况下利用移动语义，提高程序的性能。
- std::forward也是一个函数模板，用于在函数转发（forwarding）时保持参数类型。它与stdmove类似，但是它能够根据传递给它的类型自动进行转发，既可以用于左值引用，也可以用于右值引用。它的主要用途是在实泛型代码时，将函数参数以原始的转发方式传递给其他函数，以保持参数的类型和值的完整性。
总结起来，std::move用于在移动语义中转移对象的所有权，而std::forward则用于完美转发函数参数，保持参数的类型。这两个函数都是为了高效和灵活地处理C++中的对象转移和函数转发而引入的，能够使代码更加简洁和高效。
当使用std::move时，我们可以将一个对象的所有权从一个对象转移到另一个对象。在下面的例子中，通过使用std::move，我们将source的所有权转移到了destination，这样我们就可以高效地移动source的内容而不是逐个复制每个元素。例如：
c++int main() {
std::vector<int> source = {1, 2, 3, 4, 5};
// 使用std::move将source的所有权转移到destination
std::vector<int> destination = std::move(source);
// source现在为空，已经移动到destination
std::cout << "Size of source: " << source.size() << std::endl; // 输出 0 // destination包含原来source元素
std::coutSize of destination: " << destination.size() << std::endl; // 输出
return 0;
}
当使用std::forward时，我们可以在函数转发中保持参数的类型。在这个例子中，我们定义了一个 processValue 函数，它接受一个右值引用参数。然后我们使用 forwardFunction 函数来转发参数，使用 std::forward 将参数完美转发给 processValue 函数。在 main 函数中，我们展示了如何使用 forwardFunction 函数来传递左值和右值，而调用 processValue 函数。通过 std::forward，我们可以在函数转发中保持参数类型的完整性。
c++// 接受参数的函数
void processValue(int&& x) {
std::cout << "Processing rvalue: " << x << std::endl;
}
// 使用std::forward转template<typename T>
void forwardFunction(T&& arg) {
processValue(std::forward<T>(arg));
}
int main() {
int value = 42;
// 传递左值，调用processValue函数
forwardFunction(value);
// 传递右值，调用processValue函数
forwardFunction(std::move(value));
return 0;
}
std::forward相比于简单地将参数传递给另一个函数而言，可以提高代码的效率，主要体现在以下几个方面：
- 避免多余的拷贝：当参数是左值（lvalue）时，使用std::forward可以将参数作为左值引用传递给下一层函数，避免产生额外的拷贝操作。如果直接传递参数，会导致参数被当作右值（rvalue）来处理，从而触发拷贝构造函数。
- 精确匹配重载函数：有时我们在一个函数中需要对传递的参数进行重载函数的调用，而这些重载函数可能接受不同的参数类型（比如一个接受左值引用，一个接受右值引用）。使用std::forward可以精确匹配原始传入参数的类型，从而调用正确的重载函数。
- 消除重载冗余：std::forward使用引用折叠规则，从而避免引入额外的重载函数，以减少代码的冗余。通过std::forward，可以将参数的左值引用和右值引用统一起来，消除了传递参数时的冗余重载处理。
总而言之，std::forward提供了一种高效的方式来将参数按照原始的值类别和修饰符转发给下一层函数，避免了多余的拷贝操作，精确匹配重载函数，并消除了重载冗余，从而提高了代码的效率。
模板类
c++// XX.h
template <typename T>
class MyTemplateClass {
private;
T data;
public:
MyTemplateClass(T value) : data(value) {} // 构造函数
void printData() {
std::cout << "Data: " << data << std::endl; // 模板类方法
}
};
// XX.cpp
MyTemplateClass<int> obj1(10); // 实例化为处理int类型的对象
MyTemplateClass<double> obj2(3.14); // 实例化为处理double类型的对象
obj1.printData(); //: Data: 10
obj2.printData(); // 输出: Data: 3.14
为什么模板类写在.h中，不在.cpp中
模版是在编译的时候实例化的，实例化需要知道模版参数的具体类型，如果把模版的声明和定义分离编译的话，那么cpp文件中的模版实现不知道T的类型，无法实例化。都写到头文件中就解决了
在C++中，模板类通常需要在头文件（.h）中进行定义和实现，而不是分离到.cpp文件中。这是由C++的编译模型和模板实例化的特性决定的。
模板类是在使用时根据实际的模板参数进行实例化的，编译器需要在编译阶段生成模板类的实例化代码。因此，编译器需要在编译阶段能够访问模板类的完整定义和现，以便为每个模板参数生成对应的实例化代码。
如果将模板和实现分离，那编译阶段只能看到模板类，无法生成实例化的代码。这将导致链接阶段找不到所需的实例化代码，进而导致链接错误。
new和malloc的区别
| new | malloc | |
|---|---|---|
| 语法 | int *p = new int(0)或int *p = new int | int *p = (int*)malloc(sizeof(int)) |
| 初始化 | 可以初始化 | 无 |
| 函数与运算法 | 操作符，返回指定类型的地址，不需类型转换 | 函数，返回void * |
| 失败返回值 | 抛出异常bad_alloc | 返回NULL |
| 构造析构调用 | 创建对象时自动调用 | 无 |
可以用malloc给一个类对象分配内存吗
malloc分配内存不会调用构造函数
new与delete实现
实际调用malloc 与 free，但区别如下：
- 申请失败后，new返回值为异常，bad_malloc，malloc返回NULL
- 对于内置数据类型一致，对于类，执行构造函数与析构函数
new 实际调用brk()与mmap()系统调用
深浅拷贝
- 浅拷贝就是增加了一个指向相同堆区的指针，这将导致在析构的时候会重复释放。默认的拷贝构造和运算符重载都是浅拷贝。
- 深拷贝是在拷贝的时候将内容申请内存，重新拷贝一份，放到内存中，指针指向这个新拷贝的部分，这样就不会出现析构的时候重复释放的问题了。
重载和重写
重载：在同一个类中，方法相同，参数数量与类型不同（静态多态性），例：构造函数，函数名相同，参数同（返回值无法判读）
重写：在父类与子类中，方法与参数都相同（动态多态性），子类对象调用该方法时，父类方法被屏蔽
虚函数作用及底层实现原理
- 实现多态性
- 公有继承（基类定义虚函数，派生类可以重写）
- 动态联编（父类指针指向子类对象时，调用子类方法）（类似函数重载（静态），重写为动态的）
c++//Base Class
class Student {
private:
int m_id;
// protected:
string m_name;
int m_gender;
public:
Student();
Student(string name, int gender, int id);
virtual ~Student(); //申明virtual方法的基类中的析构函数必须为虚函数，否则在释放指针指向的派生类对象时，将调用基类的析构函数造成错误
virtual void Show_Info();
};
//Derived Class
class Student_Zju : public Student{
private:
int m_ser_num;
public:
Student_Zju();
Student_Zju(string name, int gender, int id, int ser_num);
virtual ~Student_Zju();
virtual void Show_Info();
};
实现机制：为每个类对象添加一个隐藏成员，保存了一个指向函数（虚函数）地址数组的指针，称为虚表指针（虚函数表）
-
如果派生类重写了基类的虚方法，该派生类虚函数表将保存重写的虚函数的地址，而不是基类的虚函数地址。
-
如果基类中的虚方法没有在派生类中重写，那么派生类将继承基类中的虚方法，而且派生类中虚函数表将保存基类中未被重写的虚函数的地址。注意，如果派生类中定义了新的虚方法，则该虚函数的地址也将被添加到派生类虚函数表中。
含有纯虚函数的类是否可以实例化
不可以，需要被派生类继承后才行
在基类中不能对虚函数给出具体的有意义的实现，就可以把它声明为纯虚函数，它的实现留给该基类的派生类去做。
c++class VirtualClass{
public:
virtual void fun1() = 0; // 纯虚函数
virtual ~VirtualClass();
};
class ClassA : public VirtualClass{
public:
virtual void fun1() { // 虚函数
printf("VirtualClass\n");
};
virtual ~VirtualClass();
};
int main(){
//编译报错，这个非法的
VirtualClass * virtualClass = new VirtualClass();//error: cannot allocate an object of abstract type 'VirtualClass'
VirtualClass * classA = new ClassA();
classA->fun1();
return 0;
}
构造函数是否可以是虚函数，析构函数为什么建议是虚函数
构造函数不可以是虚函数，如果构造函数时虚函数，那么调用构造函数就需要去找vptr，而此时vptr还没有初始化
析构函数需要是虚函数，当父类指针指向子类对象时，释放子类对象时，若父类析构非虚，会调用父类析构，子类相较于父类多出的方法不会被析构
c++BaseClass* pObj = new SubClass();
delete pObj;
- 若析构函数是虚函数(即加上virtual关键词)，delete时基类和子类都会被释放
- 若析构函数不是虚函数(即不加virtual关键词)，delete时只释放基类，不释放子类，会造成内存泄漏问题
虚函数表与内存模型
假如一个类有虚函数，当我们构建这个类的实例时，将会额外分配一个指向该类虚函数表的指针，当我们用父类的指针来操作一个子类的时候，这个指向虚函数表的指针就派上用场了，它指明了此时应该使用哪个虚函数表
C++虚函数表的位置——从内存的角度 - 知乎 (zhihu.com)
- 每个类,只要含有虚函数,new出来的对象就包含一个虚函数指针,指向这个类的虚函数表(这个虚函数表一个类用一张)
- 子类继承父类,会形成一个新的虚函数表,但是虚函数的实际地址还是用的父类的,如果子类重写了某个虚函数,那么子类的虚函数表中存放的就是重写的虚函数的地址
- 不同类之间可以通过强制转型调用其他类的虚函数
如何判断一个方法来自父类还是子类
方法一：可以在父类或子类的相应方法print()一个标记 方法二：dynamic_cast
c++class Tfather {
public:
virtual void f() { cout << "father's f()" << endl; }
};
class Tson : public Tfather {
public:
void f() { cout << "son's f()" << endl; }
int data; // 我是子类独有成员
};
int main() {
Tfather father;
Tson son;
son.data = 123;
Tfather *pf;
Tson *ps;
/* 上行转换：没有问题，多态有效 */
ps = &son;
pf = dynamic_cast<Tfather *>(ps);
pf->f();
/* 下行转换（pf实际指向子类对象）：没有问题 */
pf = &son;
ps = dynamic_cast<Tson *>(pf);
ps->f();
cout << ps->data << endl; // 访问子类独有成员有效
/* 下行转换（pf实际指向父类对象）：含有不安全操作，dynamic_cast发挥作用返回NULL */
pf = &father;
ps = dynamic_cast<Tson *>(pf);
assert(ps != NULL); // 违背断言，阻止以下不安全操作
ps->f();
cout << ps->data << endl; // 不安全操作，对象实例根本没有data成员
/* 下行转换（pf实际指向父类对象）：含有不安全操作，static_cast无视 */
pf = &father;
ps = static_cast<Tson *>(pf);
assert(ps != NULL);
ps->f();
cout << ps->data << endl; // 不安全操作，对象实例根本没有data成员
system("pause");
}
菱形继承
D类的对象不确定调用哪个父类的方法
c++class Animal{
private:
int weight;
public:
virtual int getWeight() {
return this->weight; // 共用虚函数
}
};
class Tiger : public Animal{};
class Lion : public Animal{};
class Liger : public Tiger, public Lion{}; // 如此定义存在问题，不确定调用哪个getWeight()
int main()
{
Liger lg;
lg.getWeight(); // 非法
lg.Lion::getWeight(); // 合法
}
c++// 解决方案
class Animal{
private:
int weight;
public:
virtual int getWeight() {
return this->weight;
}
};
class Tiger : virtual public Animal{}; // 加入virtual虚继承
class Lion : virtual public Animal{};
class Liger : public Tiger, public Lion{};
int main()
{
Liger lg;
lg.getWeight();
}
拷贝构造函数与赋值构造函数
区别：赋值时对象是否已经存在
C++每一个类提供默认的拷贝构造函数，但成员变量涉及指针时，浅拷贝带来问题，需要自定义深拷贝
拷贝构造函数调用的情况：
c++// 拷贝构造
Complex c2(c1); //拷贝构造函数初始化
Complex c2 = c1; //首次创建对象是初始化，不是赋值语句
void Func(Class a) {balabala} //调用函数时，Class将实参拷贝构造为形参
// 对象作为函数参数
void func(Class class);
// 函数返回值为一个非引用型对象
return A_class;
// 使用一个对象初始化另一个对象
Clsss a = b; // （a不存在，需要构造）
// 有参构造函数
Class c(a); //调用拷贝构造函数
重载的赋值运算符调用情况：
c++// 赋值构造
Complex c1, c2; //默认构造函数
c1 = c2 ; //重载的赋值运算符，已经存在对象，不是拷贝构造
// 运算符重载
A& operator = (const A& other) {}
// 赋值
Class a;
a = b; // 对象存在，调用赋值
c++#include <iostream>
class MyClass {
private:
int privateMember;
public:
// 默认构造函数
MyClass() : privateMember(0) {
std::cout << "Default constructor called." << std::endl;
}
// 拷贝构造函数
MyClass(const MyClass& other) : privateMember(other.privateMember) {
std::cout << "Copy constructor called." << std::endl;
}
// 赋值构造函数
MyClass& operator=(const MyClass& other) {
std::cout << "Assignment operator called." << std::endl;
if (this == &other) {
return *this;
}
privateMember = other.privateMember;
return *this;
}
// 获取私有成员的值
int getPrivateMember() const {
return privateMember;
}
// 设置私有成员的值
void setPrivateMember(int value) {
privateMember = value;
}
};
int main() {
MyClass obj1; // 调用默认构造函数
obj1.setPrivateMember(42);
MyClass obj2 = obj1; // 调用拷贝构造函数
MyClass obj3;
obj3 = obj1; // 调用赋值构造函数
std::cout << "Value of obj1's private member: " << obj1.getPrivateMember() << std::endl;
std::cout << "Value of obj2's private member: " << obj2.getPrivateMember() << std::endl;
std::cout << "Value of obj3's private member: " << obj3.getPrivateMember() << std::endl;
return 0;
}
C++如何实现只在栈上实例化对象
(24条消息) 如何限制对象只能建立在堆上或者栈上_舒夜无痕的博客-CSDN博客
c++class A { // 只在堆heap上建立对象，调用create()函数在堆上创建类A对象，调用destory()函数释放内存
protected:
A(){}
~A(){}
public:
static A* create() {
return new A();
}
void destory() {
delete this;
}
};
只有使用new运算符，对象才会建立在堆上，因此，只要禁用new运算符就可以实现类对象只能建立在栈上。将operator new()设为私有即可。
c++class A { // 只在栈stack上建立对象
private:
void* operator new(size_t t){} // 注意函数的第一个参数和返回值都是固定的
void operator delete(void* ptr){} // 重载了new就需要重载delete
public:
A(){}
~A(){}
};
如何避免内存泄漏，用过什么智能指针，智能指针的实现原理
C++没有内存回收机制，每次程序员new出来的对象需要手动delete，流程复杂时可能会漏掉delete，导致内存泄漏
智能指针：
- shared_ptr（引用计数，新增++，过期--，0释放）
- unique_ptr（独占式，不允许复制拷贝）（线程安全）
- weak_ptr（解决循环引用计数问题）（循环引用计数：两个智能指针互相指向对方，造成内存泄漏。需要weak_ptr，将其中的一个指针设置为weak_ptr。）（因为weak_ptr没有共享资源，它的构造函数不会引起智能指针引用计数的变化）
c++#include <iostream>
#include <memory> // 头文件
using namespace std;
class A {
public:
A(int count) { // 构造
_nCount = count;
}
~A(){} // 析构
void Print() {
cout<<"count:"<<_nCount<<endl; // 公有方法
}
private:
int _nCount; // 私有成员变量
};
int main() {
shared_ptr<A> p(new A(10)); // 初始化，堆上新建一个类，p为智能指针
p->Print(); // 调用
return 0;
}
c++#include <memory>
shared_ptr<int> p = make_shared<int> (100); // 指针指向一块存放100的地址，推荐使用
shared_ptr<int> p {new int(100)}; // 第二种创建方式
c++#include <memory>
unique_ptr<int> p = make_unique<int>(100); // 独占指针
unique_ptr<int> p1(p.release()); // 将p的指向及所有权转移到p1
unique_ptr<int> p1 = std::move(p); // 同样的
shared_ptr多线程安全问题
- 同一个shared_ptr被多个线程“读”是安全的；
- 同一个shared_ptr被多个线程“写”是不安全的；
- 共享引用计数的不同的shared_ptr被多个线程”写“ 是安全的；
引用计数是线程安全的，但在多个线程中对其进行修改不安全
shared_ptr是线程安全的吗？-腾讯云开发者社区-腾讯云 (tencent.com)
当我们谈论shared_ptr的线程安全性时，我们在谈论什么？ - 掘金 (juejin.cn)
内存泄漏检测
内存泄漏（Memory Leak）是指程序中已动态分配的堆内存由于某种原因程序未释放或无法释放，造成系统内存的浪费，导致程序运行速度减慢甚至系统崩溃等严重后果
避免内存泄露的方法
- 有良好的编码习惯，动态开辟内存空间，及时释放内存
- 采用智能指针来避免内存泄露
- 采用静态分析技术、源代码插装技术等进行检测
同步I/O与异步I/O
同步I/O是指程序在进行输入/输出操作时会阻塞当前线程，直到操作完成才继续执行后续代码（死等）
异步I/O是指程序在进行输入/输出操作时不会阻塞当前线程，而是继续执行后续代码，并通过回调或者轮询等机制来获取I/O操作的结果（让出权限等待唤醒）
- 同步I/O简单直观，代码编写相对容易，但会阻塞线程造成资源浪费。
- 异步I/O能够充分利用系统资源，提高并发性能，但需要处理回调和事件驱动等复杂性。
STL常见容器及其内部实现的数据结构
| 名称 | 描述 | 存储结构 | 方法 |
|---|---|---|---|
| vector | 动态分配的数组 | 顺序，array | v.capacity(); //容器容量--v.size(); //容器大小--v.at(int idx); //用法和[]运算符相同--v.push_back(); //尾部插入--v.pop_back(); //尾部删除--v.front(); //获取头部元素--v.back(); //获取尾部元素--v.begin(); //头元素的迭代器--v.end(); //尾部元素的迭代器--v.insert(pos,elem); //pos是vector的插入元素的位置--v.insert(pos, n, elem) //在位置pos上插入n个元素elem--v.insert(pos, begin, end);--v.erase(pos); //移除pos位置上的元素，返回下一个数据的位置--v.erase(begin, end); //移除[begin, end)区间的数据，返回下一个元素的位置--reverse(pos1, pos2); //将vector中的pos1~pos2的元素逆序存储 |
| list | 双向链表 | 离散 | (1) 元素访问：lt.front();--lt.back();--lt.begin();--lt.end();--(2) 添加元素：--lt.push_back();--lt.push_front();--lt.insert(pos, elem);--lt.insert(pos, n , elem);--lt.insert(pos, begin, end);--lt.pop_back();--lt.pop_front();--lt.erase(begin, end);--lt.erase(elem);--(3)sort()函数、merge()函数、splice()函数：--sort()函数就是对list中的元素进行排序;--merge()函数的功能是：将两个容器合并，合并成功后会按从小到大的顺序排列;--比如：lt1.merge(lt2); lt1容器中的元素全都合并到容器lt2中。--splice()函数的功能是：可以指定合并位置，但是不能自动排序！ |
| stack | 栈 | 用list或deque实现 | |
| quque | 队列 | 用list或deque实现 | |
| deque | 双端队列 | 分段连续（多个vector连续） | (1) 元素访问：d[i];--d.at[i];--d.front();--d.back();--d.begin();--d.end();--添加元素：d.push_back();--d.push_front();--d.insert(pos,elem); //pos是vector的插入元素的位置--d.insert(pos, n, elem) //在位置pos上插入n个元素elem--d.insert(pos, begin, end);--删除元素：d.pop_back();--d.pop_front();--d.erase(pos); //移除pos位置上的元素，返回下一个数据的位置--d.erase(begin, end); //移除[begin, end)区间的数据，返回下一个元素的位置 |
| priority_queue | 优先级队列 | vector | |
| set | 集合（有序不重复） | 红黑树（弱平衡二叉搜索树，二分查找法搜索高效） | s.size(); //元素的数目--s.max_size(); //可容纳的最大元素的数量--s.empty(); //判断容器是否为空--s.find(elem); //返回值是迭代器类型--s.count(elem); //elem的个数，要么是1，要么是0，multiset可以大于一begin 返回一个指向集合中第一个元素的迭代器。--cbegin 返回指向集合中第一个元素的const迭代器。--end 返回指向末尾的迭代器。--cend 返回指向末尾的常量迭代器。--rbegin 返回指向末尾的反向迭代器。--rend 返回指向起点的反向迭代器。--crbegin 返回指向末尾的常量反向迭代器。--crend 返回指向起点的常量反向迭代器。--s.insert(elem);--s.insert(pos, elem);--s.insert(begin, end);--s.erase(pos);--s.erase(begin,end);--s.erase(elem);--s.clear();//清除a中所有元素； |
| multiset | 集合（有序可重复） | 红黑树 | |
| unordered_set | 集合（无序不重复） | hash | |
| map | 键值对（有序不重复） | 红黑树 | |
| multimap | 键值对（有序可重复） | 红黑树 | |
| unordered_map | 键值对（无序不重复） | hash | |
| hash_map | 哈希表，类似map，速度更快 | hash |
deque底层数据结构
红黑树
非严格的平衡搜索二叉树，有自动排序的功能
sort()
仅支持随机访问的数据结构进行快速排序，如vector、deque、array
c++bool func(int a, int b) {
return a > b;
}
sort(vec.begin(), vec.end(), func); // 升序排列
partial_sort()
对部分元素进行升序/降序排列，利用大顶堆/小顶堆实现，堆空间为n
c++bool func(int a, int b) {
return a > b;
}
int n = 4; // 需要排序的数量
partial_sort(vec.begin(), vec.begin() + n, vec.end(), func); // 仅排序其中的n个元素
is_sorted()
c++bool func(int a, int b) {
return a > b;
}
bool result = is_sorted(vec.begin(), vec.end(), func()) // 返回值为bool，是否按照func定义的顺序排序
is_sorted_until()
c++bool func(int a, int b) {
return a > b;
}
auto it = is_sorted(vec.begin(), vec.end(), func()) // 返回值：指向序列中第一个破坏 comp 排序规则的元素迭代器
find()
c++vector<int> vec{ 10,20,30,40,50 };
auto it = find(vec.begin(), vec.end(), 30); // 起始、终止迭代器、查找的值
if (it != myvector.end())
cout << "查找成功：" << *it;
else
cout << "查找失败";
return 0;
find_if()
按照自定义谓词查找
c++bool mycomp(int i) {
return ((i % 2) == 1);
}
vector<int> myvector{ 4,2,3,1,5 };
auto it = find_if(myvector.begin(), myvector.end(), mycomp());
使用vector如何避免频繁的内存重新分配
内存分配的过程：
- 分配新的内存块，在大部分实现中，vector和string的容量每次以2为因数增长。也就是说，当容器必须扩展时，它们的容量每次翻倍。
- 把所有元素从容器的旧内存拷贝到它的新内存。
- 销毁旧内存中的对象。
- 回收旧内存。
解决方案：
- 预分配内存：在创建 vector 对象时，可以使用 reserve() 方法来预分配内存空间，以避免频繁扩容。
- 合理选择初始容量：在创建 vector 对象时，可以根据数据量的大小估算出合理的初始容量，这样可以尽可能减少扩容的次数。
- 优化算法：尽可能使用时间复杂度低的算法，避免数据量过大时的性能问题。
vector resize()与reserve()
- resize(Container::size_type n)强制把容器改为容纳n个元素。调用resize之后，size将会返回n。如果n小于当前大小，容器尾部的元素会被销毁。如果n大于当前大小，新默认构造的元素会添加到容器尾部。如果n大于当前容量，在元素加入之前会发生重新分配。
- reserve(Container::size_type n)强制容器把它的容量改为至少n，提供的n不小于当前大小。这一般强迫进行一次重新分配，因为容量需要增加。（如果n小于当前容量，vector忽略它，这个调用什么都不做，string可能把它的容量减少为size()和n中大的数，但string的大小没有改变。）
vector的扩容系数为什么是1.5或2
面试题：C++vector的动态扩容，为何是1.5倍或者是2倍_vector扩容_森明帮大于黑虎帮的博客-CSDN博客
扩容原理为：申请新空间，拷贝元素，释放旧空间，理想的分配方案是在第N次扩容时如果能复用之前N-1次释放的空间就太好了，如果按照2倍方式扩容，第i次扩容空间大小如下：
可以看到，每次扩容时，前面释放的空间都不能使用。比如：第4次扩容时，前2次空间已经释放，第3次空间还没有释放(开辟新空间、拷贝元素、释放旧空间)，即前面释放的空间只有1 + 2 = 3，假设第3次空间已经释放才只有1+2+4=7，而第四次需要8个空间，因此无法使用之前已释放的空间，但是按照小于2倍方式扩容，多次扩容之后就可以复用之前释放的空间了。
Linux中：内存heap区域被事先分配为2^n大小，以2的倍数扩容可以方便地进行分配
Win中：内存被free的区域会被系统立即合并，以1.5被分配可以使用被释放的内存
迭代器
作用：对于不同的数据结构，通过迭代器均可实现遍历，多态
[注意]：迭代器只能前进不能后退
迭代器失效的情况
迭代器失效分三种情况考虑，也是分三种数据结构考虑，分别为数组型，链表型，树型数据结构。
**数组型数据结构：**该数据结构的元素是分配在连续的内存中，insert和erase操作，都会使得删除点和插入点之后的元素挪位置，所以，插入点和删除掉之后的迭代器全部失效，也就是说insert(*iter)(或erase(*iter))，然后在iter++，是没有意义的。解决方法：erase(*iter)的返回值是下一个有效迭代器的值。 iter =cont.erase(iter);
**链表型数据结构：**对于list型的数据结构，使用了不连续分配的内存，删除运算使指向删除位置的迭代器失效，但是不会失效其他迭代器.解决办法两种，erase(*iter)会返回下一个有效迭代器的值，或者erase(iter++).
树形数据结构： 使用红黑树来存储数据，插入不会使得任何迭代器失效；删除运算使指向删除位置的迭代器失效，但是不会失效其他迭代器.erase迭代器只是被删元素的迭代器失效，但是返回值为void，所以要采用erase(iter++)的方式删除迭代器。
注意：经过erase(iter)之后的迭代器完全失效，该迭代器iter不能参与任何运算，包括iter++,*ite
内联函数inline
作用：将函数入栈出栈的调用开销减少，（将函数展开为代码）
优势：
- 对于简单函数而言加快运行速度，省去了参数压栈、栈帧开辟与回收，结果返回等
- 相当于有类型检查的宏定义，且可以调试
缺陷：
- 以膨胀代码为代价
- 不能包含循环、递归等复杂操作
- 是否内联，程序员不可控。内联函数只是对编译器的建议，是否对函数内联，决定权在于编译器。
- 可能影响代码的执行效率，因为内联函数的本质是把函数体直接嵌入到调用处，这样会导致代码的大小增加，从而可能导致缓存命中率下降，影响执行效率。
哈希表
查表，要枚举的话时间复杂度是O(n)，但如果使用哈希表的话， 只需要O(1)就可以做到。我们只需要初始化把这所学校里学生的名字都存在哈希表里，在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
哈希碰撞：
解决方法：
链表法（tableSize=dataSize）
线性探测法（tableSize>=dataSize）将冲突的元素放到下一个空位中
哈希操作
- 查找：当使用键进行查找时，哈希表会使用键的哈希值来确定其在哈希表中的位置，并进一步比较键的值来判断是否匹配。如果键相同，那么可以通过哈希值直接找到对应的位置，并返回存储在该位置上的值。
- 插入：在向哈希表中插入键值对时，哈希表首先会计算键的哈希值，并根据哈希值找到对应的位置。然后，它会检查该位置上是否已经存在相同的键。如果存在相同的键，则可以选择更新现有的值，或者根据具体的实现策略来处理冲突。
- 删除：当从哈希表中删除一个键值对时，哈希表会使用键的哈希值来定位该键所在的位置。如果在该位置上找到了匹配的键，就将其从哈希表中删除。
当两个对象映射到同一个哈希地址时，是否说明这两个对象相同
当两个对象产生哈希冲突时，它们被映射到了相同的哈希地址上，但并不能确定它们的内容是否相同。两个不同的对象完全可以具有相同的哈希值，因为哈希值只是一个对输入对象进行计算得出的结果。
要确定两个对象是否相同，通常需要使用其他方法，如比较它们的内容、引用或标识符等。哈希地址相同并不代表对象相同，只能说它们在哈希函数中产生了冲突。
哈希表如何解决键值冲突
哈希表（散列表）根据(Key value)直接进行访问的数据结构。映射函数叫做散列函数，存放记录的数组叫做散列表。
哈希值是通过哈希函数计算出来的，通过哈希函数计算出来的哈希值相同，就是哈希冲突，不能完全避免
解决方案：
- 开放定址法：发现冲突后寻找下一个空闲散列表位置
- 再哈希法：利用不同的哈希函数再次计算哈希值（多轮）
- 链地址法：每个哈希表节点都有一个next指针，多个哈希表节点可以用next指针构成一个单向链表，被分配到同一个索引上的多个节点可以用这个单向链表连接起来，因而查找、插入和删除主要在同义词链中进行。
- 公共溢出区法：冲突放入溢出表
CMake是如何包含文件目录的
cmaketarget_include_directories(test PRIVATE ${YOUR_DIRECTORY}) #添加要包含的目录 set(SOURCES file.cpp file2.cpp ${YOUR_DIRECTORY}/file1.h ${YOUR_DIRECTORY}/file2.h) #将头文件添加到当前目标的源文件列表中 add_executable(test ${SOURCES})
extern c
C++不能直接调用C编译器编译的代码
在C++中可能调用C的代码段用关键字进行包裹，例子如下
extern "C" 修饰一段 C++ 代码，让编译器以处理 C 语言代码的方式来处理修饰的 C++ 代码。
c++// FUNC.h通用模板
#ifndef __INCvxWorksh /*防止该头文件被重复引用*/
#define __INCvxWorksh
#ifdef __cplusplus //告诉编译器，这部分代码按C语言的格式进行编译，而不是C++的
extern "C"{
#endif
/* C语言实现的部分函数申明 */
/* C语言实现的部分函数申明 */
#ifdef __cplusplus
}
#endif
#endif /*end of __INCvxWorksh*/
extern "C"的主要作用就是为了能够正确实现C++代码调用其他C语言代码。加上extern "C"后，会指示编译器这部分代码按C语言（而不是C++）的方式进行编译。由于C++支持函数重载，因此编译器编译函数的过程中会将函数的参数类型也加到编译后的代码中，而不仅仅是函数名；而C语言并不支持函数重载，因此编译C语言代码的函数时不会带上函数的参数类型，一般只包括函数名。
c++//moduleA.h
int fun(int, int);
//moduleA.C
#include"moduleA"
int fun(int a, int b)
{
return a+b;
}
//moduleB.h
#ifdef __cplusplus //而这一部分就是告诉编译器，如果定义了__cplusplus(即如果是cpp文件，
extern "C"{ //因为cpp文件默认定义了该宏),则采用C语言方式进行编译
#include"moduleA.h"
#endif
… //其他代码
#ifdef __cplusplus
}
#endif
//moduleB.cpp
#include"moduleB.h"
int main()
{
cout<<fun(2,3)<<endl;
}
总结
通常在C++ 中，假如需要使用C语言中的库文件的话，可以使用extern "C"去包含c编写的头文件
设计模式
单例模式
在整个系统生命周期内，保证一个类只能产生一个实例，确保该类的唯一性。成员函数均为static
工厂模式
抽象出一个工厂，工厂有不同的产线继承自工厂类，对于产品抽象出产品类
字符串string char*互转
c// char[] 转 char*
char ch[]="abcdef";
char *s = ch;
// char* 转 char[]
char *s="abcdef";
char ch[100];
strcpy(ch,s);
// string 转 char[]
string str= "abcdef";
char ch[20];
int i;
for( i=0;i<=str.length();i++){
ch[i] = str[i];
if(i==str.length()) c[i] = '\0';
}
// char[] 转 string
string str;
char ch[20] = "abcdef";
str = ch;
// string 转 char*
string str = "abcdef";
const char* p = (char*)str.data(); // data()仅返回字符串内容，而不含有结束符’\0’
string str=“abcdef”;
const char *p = str.c_str();
//使用char * p=(char*)str.c_str()效果相同
string str=“abcdef”+ '\0';
char *p= new char[str.length()+1];
str.copy(p,str.length(),0); // 要想指针指向内容及地址不改变，使用该方式
// char* 转 string
string str;
char *p = "abcdef";
str = p;
char *p = "abcdef";
string str;
str.assign(p,strlen(p)); // 要想指针指向内容及地址不改变，使用该方式
C++11、C++14、C++17、C++20 新特性
- C++11 新特新 - static_assert 编译时断言 - 新增加类型 long long ，unsigned long long，char16_t，char32_t，原始字符串 - auto - decltype - 委托构造函数 - constexpr - 模板别名 - alignas - alignof - 原子操作库 - nullptr - 显示转换运算符 - 继承构造函数 - 变参数模板 - 列表初始化 - 右值引用 - Lambda 表达式 - override、final - unique_ptr、shared_ptr - initializer_list - array、unordered_map、unordered_set - 线程支持库
- C++14 新特新 - 二进制字面量 - 泛型 Lambda 表达式 - 带初始化/泛化的 Lambda 捕获 - 变量模板 - [[deprecated]]属性 - std::make_unique - std::shared_timed_mutex、std::shared_lock - std::quoted - std::integer_sequence - std::exchange
- C++17 新特新 - 构造函数模板推导 - 结构化绑定 - 内联变量 - 折叠表达式 - 字符串转换 - std::shared_mutex
- C++20 新特新 - 允许 Lambda 捕获 [=, this] - 三路比较运算符 - char8_t - 立即函数（consteval） - 协程 - constinit
C++11中的atomic
C++11引入了一组原子类型（Atomic Types），用于解决多线程环境下的并发访问问题。原子类型保证了对变量的读写操作是原子的，即不会发生数据竞争。
c++#include <iostream>
#include <atomic>
#include <thread>
std::atomic<int> counter(0);
void incrementCounter() {
for (int i = 0; i < 1000; ++i) {
counter.fetch_add(1, std::memory_order_relaxed);
}
}
int main() {
std::thread t1(incrementCounter);
std::thread t2(incrementCounter);
t1.join();
t2.join();
std::cout << "Counter value: " << counter << std::endl;
return 0;
}
C++多线程
pthread_create
创建子线程，并注册回调函数
pthread_join
在主线程中调用，等待子线程执行完毕后，释放子线程资源，再执行join后的代码
pthread_detach
主线程在调用pthread_detach(子线程ID) 与pthread_exit(NULL)后，不用等待Join才可释放子线程资源，在子线程结束运行前，主线程可以执行其他功能，子线程运行结束后资源由OS而非主线程释放
pthread_cancel
在主线程中杀死子线程（通过系统调用，延迟杀死线程）
pthread_equal
比较两个线程ID是否一致
父子进程fork()
当一个进程调用 fork 函数生成另一个进程，原进程就称为父进程，新生成的进程则称为子进程。
c++#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
int main(int argc, char * argv[])
{
int pid;
/* fork another process */
pid = fork();
if (pid < 0)
{
/* error occurred */
fprintf(stderr,"Fork Failed!");
exit(-1);
}
else if (pid == 0)
{
/* child process */
printf("This is Child Process!\n");
}
else
{
/* parent process */
printf("This is Parent Process!\n");
/* parent will wait for the child to complete*/
wait(NULL);
printf("Child Complete!\n");
}
}
可以建立一个新进程，把当前的进程分为父进程和子进程，新进程称为子进程，而原进程称为父进程。fork调用一次，返回两次，这两个返回分别带回它们各自的返回值，其中在父进程中的返回值是子进程的PID，而子进程中的返回值则返回 0。因此，可以通过返回值来判定该进程是父进程还是子进程。
孤儿进程
父进程释放，子进程还在，内核接管，没有危害
僵尸进程
子进程退出，父进程不知道，此时子进程还占用着资源
在 Linux 环境中，我们是通过 fork 函数来创建子进程的。创建完毕之后，父子进程独立运行，父进程无法预知子进程什么时候结束。通常情况下，子进程退出后，父进程会使用 wait 或 waitpid 函数进行回收子进程的资源，并获得子进程的终止状态。但是，如果父进程先于子进程结束，则子进程成为孤儿进程。孤儿进程将被 init 进程（进程号为1）领养，并由 init 进程对孤儿进程完成状态收集工作。而如果子进程先于父进程退出，同时父进程太忙了，无瑕回收子进程的资源，子进程残留资源（PCB）存放于内核中，变成僵尸（Zombie）进程
解决方案：
- 父进程在子进程退出时调用wait()/waitpid()函数来回收子进程的资源
- fork一个孙子进程，然后将子进程变为一个孤儿进程可以避免僵尸进程的产生
- 杀死这个僵尸进程的父进程。那么该僵尸进程就会被守护进程给领养。从而守护进程，会对这个僵尸进程的内核区资源进行回收。
僵尸进程其实已经就是退出的进程，因此无法再利用kill命令杀死僵尸进程。僵尸进程的罪魁祸首是父进程没有回收它的资源，那我们可以想办法它其它进程去回收僵尸进程的资源，这个进程就是 init 进程。因此，我们可以直接杀死父进程，init 进程就会很善良地把那些僵尸进程领养过来，并合理的回收它们的资源，那些僵尸进程就得到了妥善的处理了。
例如，如果 PID 5878 是一个僵尸进程，它的父进程是 PID 4809，那么要杀死僵尸进程 （5878），您可以结束父进程 （4809）：
$ sudo kill -9 4809 #4809 is the parent, not the zombie
守护进程
前台进程是在终端中运行的命令，那么该终端就为进程的控制终端，一旦这个终端关闭，这个进程也随着消失
- 而守护进程（Daemon），也就是我们平时说的后台进程，是运行在后台的一种特殊进程，不受终端控制，它不需要终端的交互
- 守护进程是一种特殊的后台进程，它通常在系统启动时自动启动，并在系统运行过程中一直运行，执行一些系统级别的任务，如监控系统资源、处理网络请求等。守护进程通常不与用户交互，也不需要终端，而是在后台默默地运行，直到系统关闭或者被显式地停止。
协程
C++20新增
协程不受操作系统调度，切换方便，轻量级
- 依赖关系：线程是由操作系统内核进行调度管理的，并且每个线程通常拥有自己的独立堆栈和上下文。而协程则是由程序员在代码中显式地定义和管理的，没有操作系统参与调度。协程依赖于某种运行时环境或者特定的库来实现调度和切换。
- 并发性能：线程属于操作系统层面的并发机制，它可以充分利用多核处理器的计算能力。每个线程都需要一定的系统资源来进行管理，因此创建大量线程可能会导致资源消耗过大。相比之下，协程是轻量级的，可以在单个线程中运行大量的协程，节省了线程切换的开销。
- 切换机制：在线程之间进行切换时，需要进行上下文的保存和恢复，这是由操作系统内核负责完成的，并且通常涉及到用户态和内核态之间的切换。而协程的切换是在用户态完成的，切换开销更小。协程通过手动选择合适的切换点，在不同的协程之间进行切换，使得程序可以在合适的时机保存和恢复中间状态。
- 同步方式：线程通常通过共享内存或者消息传递来进行通信和同步。而协程则通常通过显式的调度和消息传递机制来实现数据共享和同步。协程之间的切换是协作性的，需要各个协程自行决定何时让出执行权。
总的来说，线程更加底层和系统级别，可以充分利用多核处理器的并行计算能力，但线程数量受限于系统资源，并且线程切换开销较大。而协程是一种高级抽象，更适合处理大量的轻型任务，并且协程之间的切换开销较小。但协程需要依赖特定的运行时环境或库的支持，无法直接利用多核处理器的并行计算能力。
网络编程
OSI网络模型
| 层级 | 名称 | 作用 | 协议 | 关键词 |
|---|---|---|---|---|
| 7 | 应用层 | 各类网络服务 | HTTP、FTP | |
| 6 | 表示层 | 数据编码、格式转换、加密 | LPP、NBSSP | |
| 5 | 会话层 | 维护会话 | SSL、TLS、DAP、LDAP | |
| 4 | 传输层 | 建立主机端到端的连接（应用间的通信） | TCP、UDP | 端口号、TCP、UDP |
| 3 | 网络层 | 路由选择，控制数据包在设备间的转发（主机间通信） | **IP、ICMP、路由器、**RIP、IGMP、OSPF | IP地址、路由器、ping通 |
| 2 | 数据链路层 | 将比特流封装成数据帧（数据帧、网卡间通信） | ARP、网卡、交换机、PPTP、L2TP、ATMP | MAC地址、网卡 |
| 1 | 物理层 | 定义电平、传输介质、物理接口 | 光纤、集线器、中继器等物理器件 |
TCP&UDP
- TCP 提供面向连接的可靠传输，UDP 提供面向无连接的不可靠传输。
- UDP 在很多实时性要求高的场景有很好的表现，而TCP在要求数据准确、对速度没有硬性要求的场景有很好的表现。
UDP
- 面向无连接（不需要三次握手和四次挥手）
- 尽最大努力交付、面向报文（每次收发都是一整个报文段）
- 没有拥塞控制不可靠（只管发不管过程和结果）
- 支持一对一、一对多、多对一和多对多的通信方式、首部开销很小（8字节）
优点是快，没有TCP各种机制，少了很多首部信息和重复确认的过程，节省了大量的网络资源。
缺点是不可靠不稳定，只管数据的发送不管过程和结果，网络不好的时候很容易造成数据丢失。
语音通话、视频会议等要求源主机要以恒定的速率发送数据报，允许网络不好的时候丢失一些数据，但不允许太大的延迟，UDP很适合这种要求。
TCP
- 面向连接（需要三次握手四次挥手）
- 单播（只能端对端的连接）
- 可靠交付（有大量的机制保护TCP连接数据的可靠性）
- 全双工通讯（允许双方同时发送信息，也是四次挥手的原由）
- 面向字节流（不保留数据报边界的情况下以字节流的方式进行传输，这也是长连接的由来。）
- 头部开销大（最少20字节）
优点是可靠、稳定，有确认、窗口、重传、拥塞控制机制，在数据传完之后，还会断开连接用来节约系统资源。
缺点是慢，效率低，占用系统资源高，在传递数据之前要先建立连接，这会消耗时间，而且在数据传递时，确认机制、重传机制、拥塞机制等都会消耗大量的时间，而且要在每台设备上维护所有的传输连接。
在要求数据准确、对速度没有硬性要求的场景有很好的表现，比如在FTP（文件传输）、HTTP/HTTPS（超文本传输），TCP很适合这种要求。
TCP三次握手四次挥手
tcp的三次挥手的作用是保证 通信双方都能够正常的收发信息；三次握手的发生阶段是在客户端连接服务器的connect阶段开始的
- 公安局：你好！陈某，听得到吗？（一次会话）
- 陈某：听到了，王哥，你能听到吗 （二次会话）
- 公安局：听到了，你过来自首吧 （开始会话）（三次会话）
-
第一次握手 客户端发起SYN包
-
第二次握手 服务器收到后，回复SYN+ACK包
-
第三次握手 客户端收到后，回复ACK包
有人可能会很疑惑为什么要进行第三次握手？ 主要原因：防止已经失效的连接请求报文突然又传送到了服务器，从而客户端建立1个连接，服务器建立2个连接
- 第一次握手： 客户端向服务器端发送报文 证明客户端的发送能力正常
- 第二次握手：服务器端接收到报文并向客户端发送报文 证明服务器端的接收能力、发送能力正常
- 第三次握手：客户端向服务器发送报文 证明客户端的接收能力正常
如果采用两次握手会出现以下情况： 客户端向服务器端发送的请求报文由于网络等原因滞留，未能发送到服务器端，此时连接请求报文失效，客户端会再次向服务器端发送请求报文，之后与服务器端建立连接，当连接释放后，由于网络通畅了，第一次客户端发送的请求报文又突然到达了服务器端，这条请求报文本该失效了，但此时服务器端误认为客户端又发送了一次连接请求，两次握手建立好连接，此时客户端忽略服务器端发来的确认，也不发送数据，造成不必要的错误和网络资源的浪费。
四次挥手
作用是将服务器和客户端的连接安全的断开，四次挥手是发生在客户端或者服务器断开连接的时候
- 张三：好的，那我先走了
- 李四：好的，那你走吧
- 李四：那我也走了？
- 张三：好的，你走吧
- 第一次挥手 客户端发出FIN包
- 第二次挥手 服务器收到后，发出ACK包，（此时双方还可以继续传输数据）
- 第三次挥手 服务器发送FIN包
- 第四次挥手 客户端收到后回复ACK包，进入超时等待状态，服务器端接收到确认报文后，会立即关闭断开
为什么客户端要等待2MSL？ 主要原因是为了保证客户端发送那个的第一个ACK报文能到到服务器，因为这个ACK报文可能丢失，并且2MSL是任何报文在网络上存在的最长时间，超过这个时间报文将被丢弃，这样新的连接中不会出现旧连接的请求报文。当服务端一段时间后无法收到最后一个ACK包时，会重发FIN包，再次进入流程
浏览器从输入 URL 开始到页面显示内容，中间发生了什么？
- DNS解析域名，获取ip端口
- 建立tcp链接
- http发送请求
- 服务器处理请求
- 服务器端返回数据
- 浏览器解析html
- 浏览器布局渲染
TCP可靠传输机理
TCP是通过序列号、检验和、确认应答信号、重发机制、连接管理、窗口控制、流量控制、拥塞控制一起保证TCP传输的可靠性的。
TCP（传输控制协议）通过以下机制来保证可靠传输：
- 应答机制：发送方在发送数据包后，会等待接收方的确认应答。如果发送方没有收到确认应答，就会重新发送数据包，直到收到确认为止。
- 序列号和确认号：TCP将每个数据包都赋予一个唯一的序列号，接收方收到数据包后会发送一个确认应答，并指定下一个期望接收的数据的序列号。发送方根据接收方的确认号知道哪些数据已经成功发送并被接收。
- 滑动窗口：发送方将数据分割为多个小的数据段，并使用滑动窗口的机制进行发送。接收方通过确认号告诉发送方数据被接收，发送方可以根据确认号调整滑动窗口的大小和发送速率。
- 重传机制：如果发送方在一定时间内未收到确认应答，就会认为数据包丢失，并进行重传。接收方在收到重复的数据包时会丢弃重复的数据，确保只有一个副本被交付给上层应用。
- 流量控制：TCP使用滑动窗口的机制来控制发送方发送数据的速率，避免发送过多的数据导致接收方无法及时处理或丢失数据。
- 拥塞控制：TCP根据网络的拥塞程度动态调整发送方的发送速率，避免过多的数据流入网络导致拥塞。TCP使用拥塞窗口大小和重传超时时间等参数来判断网络的拥塞情况，并采取相应的措施，如减小发送速率或等待较长时间进行重传。
TCP 粘包
TCP基于字节流，无法判断发送方报文段边界
造成粘包的因素有很多，有可能是发送方造成的，也有可能是接收方造成的。比如接收方在接收缓存中读取数据不及时，在下一个数据包到达之前没有读取上一个，可能也会造成读取到超过一个数据包的情况。多个数据包被连续存储于连续的缓存中，在对数据包进行读取时由于无法确定发生方的发送边界
发送端可能堆积了两次数据，每次100字节一共在发送缓存堆积了200字节的数据，而接收方在接收缓存中一次读取120字节的数据，这时候接收端读取的数据中就包括了下一个报文段的头部，造成了粘包。
解决粘包的方法：
- 发送方关闭Nagle算法，使用TCP_NODELAY选项关闭Nagle功能
- 发送定长的数据包。每个数据包的长度一样，接收方可以很容易区分数据包的边界
- 数据包末尾加上\r\n标记，模仿FTP协议，但问题在于如果数据正文中也含有\r\n，则会误判为消息的边界
- 数据包头部加上数据包的长度。数据包头部定长4字节，可以存储数据包的整体长度
Linux
Linux嵌入式驱动开发的流程
- 了解硬件设备及其规范：首先要对目标硬件设备进行研究，包括芯片型号、外设接口、寄存器规范等。同时，对于设备的功能和特性也需要有基本的了解。
- 编写设备树（Device Tree）描述文件：Linux内核使用设备树来描述硬件设备的信息。需要编写设备树描述文件，以便内核能够识别和配置硬件设备。
- 编写驱动程序源码：根据设备的规格和需求，编写对应的驱动程序源码。通常需要涉及到底层寄存器的读写、中断处理、设备初始化和资源分配等操作。
- 将驱动程序源码添加到内核源码树：将驱动程序源码添加到Linux内核源码树，并在内核配置选项中选择该驱动模块进行编译。
- 构建并刷写内核镜像：完成驱动程序源码的添加和内核配置后，进行内核的构建。通过编译得到的内核镜像可以刷写到目标嵌入式设备上。
- 调试和测试：将构建好的内核镜像刷写到目标设备，并进行调试和测试。检查设备与驱动之间的通信，确保驱动程序能够正确地初始化设备并提供所需的功能。
- 优化和性能测试：根据实际使用情况对驱动程序进行优化，并进行性能测试。通过性能测试来评估驱动程序的性能，并进行必要的调整和优化。
Linux内核的组成
五部分：进程管理、内存管理、进程间通信、虚拟文件系统、网络接口
1.进程管理与调度：
2.内存管理：Linux内存管理对于每个进程完成从虚拟内存到物理内存的转换
3.虚拟文件系统：隐藏硬件的细节，采用vfs_read，vfs_write等接口
4.网络接口：分为网络协议和网络驱动程序
5.进程间通信：信号量、共享内存、消息队列、管道等，实现资源互斥、同步
系统调用read() write()，内核具体做了哪些事情
用户空间read()-->内核空间sys_read()-->scull_fops.read-->scull_read()；
过程分为两个部分：用户空间的处理和内核空间的处理。
在用户空间中通过 0x80 中断的方式将控制权交给内核处理，
内核接管后，经过6个层次的处理最后将请求交给磁盘，由磁盘完成最终的数据拷贝操作。在这个过程中，调用了一系列的内核函数。
系统调用与普通函数调用的区别
| 类别 | 系统调用 | 函数调用 |
|---|---|---|
| 简介 | 调用内核的服务 | 调用函数库中的一个程序 |
| 涉及对象 | 程序与内核 | 用户与程序 |
| 运行空间 | 内核地址空间 | 用户地址空间 |
| 开销 | 上下文切换，开销大 | 小 |
Bootloader内核 、根文件的关系
启动顺序：bootloader->linuxkernel->rootfile
u-boot：初始化硬件，将内核装载入RAM，设置SP与PC，准备启动内核
kernel：（底层驱动向内核注册，上层应用向内核调用）启动并挂载rootfile（存放了文件、库、命令）
rootfile：业务涉及的文件系统
Bootloader启动过程
上电后运行的第一个程序：bootloader（u-boot）（universal bootloader）
- 典型嵌入式系统的部署：uboot程序（类似BIOS）部署在Flash(能作为启动设备的NorFlash)上、OS部署在FLash(嵌入式系统中用Flash代替了硬盘)上、内存在掉电时无作用，CPU在掉电时不工作。
- 启动过程：嵌入式系统上电后先执行uboot、然后uboot负责初始化DDR，初始化Flash，然后将OS从Flash中读取到DDR中，然后启动OS(OS启动后uboot就无用了) 总结：嵌入式系统和PC机的启动过程几乎没有两样，只是BIOS成了uboot，硬盘成了Flash。
Stage1（汇编实现，依赖cpu体系结构初始化）
进行硬件的初始化（watchdog,ram初始化） 为Stage2加载代码准备RAM空间 复制Stage2阶段代码到RAM空间 设置好栈 跳转到第二阶段代码的入口点
Stage2（c语言实现，具有好的可读性和移植性）
初始化该阶段所用到的硬件设备。 检测系统内存映射。 将uImage ,Rootfs，dtb文件从flash读取到RAM内存中。 设置内核启动参数。（如通过寄存器传递设备树文件的内存地址）
Linux启动流程
- 引导加载程序（Bootloader）启动：U-Boot 被加载到内存中执行。 U-Boot 提供了一个命令行界面，用户可以在这个界面上进行配置和操作。
- 加载内核和备树文件：通过 U-Boot 的命令，加载 Linux 内核kernel）和设备树（device tree）文件到内存中4. 启动 Linux 内核：U-Boot控制权交给 Linux 内核，内核开始执行。内核会初始化系统硬设置页表、启动调度器等。
- 启动 init 进：在内核初始化完成后，内核会执行 init 进程，init 进程是用户空间的第一个进程。 init 进程负责启动其他系统服务，并根据配置加载所需的模块。
- 用户空间初始化：init 进程会根据配置启动用户空间的各个进程和服务，完成系统的初始化。
设备树
Linux设备树（Device Tree）是一种描述硬件设备和设备间关系的数据结构，用于在嵌入式系统中配置和管理硬件。它是一种与平台无关的机制，它将硬件设备的相关信息以一种可移植的格式储存在一个或多个设备树文件中。
设备树文件是以一种层级结构的形式描述硬件设备及其属性。它包含了设备的类型、寄存器地址、中断、时钟等信息，以及设备间的关系和依赖关系。通过解析设备树文件，内核可以获取设备的配置信息，并正确地初始化和管理硬件设备。
Linux 命令
搜索：
grep *.c
grep -n "linux" test.txt // 查找文件中的关键字并显示行号
搜索文件
find /home/user/dir -type f -name "*.c"
-type f表示只搜索文件，而不包括目录
查看文件内容：
cat：将原文显示
进程：
ps：查看进程
$ ps -ax PID TTY STAT TIME COMMAND 1 ? Ss 0:01 /usr/lib/systemd/systemd rhgb --switched-root --sys 2 ? S 0:00 [kthreadd] 3 ? I< 0:00 [rcu_gp] 4 ? I< 0:00 [rcu_par_gp]
pstree：查看父子进程关系
$ pstree -psn systemd(1)─┬─systemd-journal(952) ├─systemd-udevd(963) ├─systemd-oomd(1137) ├─systemd-resolve(1138) ├─systemd-userdbd(1139)─┬─systemd-userwor(12707) │ ├─systemd-userwor(12714) │ └─systemd-userwor(12715) ├─auditd(1140)───{auditd}(1141) ├─dbus-broker-lau(1164)───dbus-broker(1165) ├─avahi-daemon(1166)───avahi-daemon(1196) ├─bluetoothd(1167)
内存占用：
free –h：系统相关RAM使用情况（物理内存、交换内存）
top：查看系统CPU、进程、内存使用情况
磁盘占用：
df -h：查看磁盘占用
关机、重启、挂起、节电：
shutdown -h now
shutdown -h +10 // 延时10min
shutdown -h 19:30
sudo reboot
sudo pm-suspend
sudo pm-powersave
手动释放内存的方法
采用TOP命令查看内存张后，采用/proc/sys/vm/drop_caches来释放内存
[root@ipa]# echo 0~3 > /proc/sys/vm/drop_caches
drop_caches的值可以是0-3之间的数字，代表不同的含义： 0：不释放（系统默认值） 1：释放页缓存 2：释放dentries和inodes 3：释放所有缓存
文件系统
查看程序依赖的动态链接库
c++#include <stdio.h>
#include <iostream>
#include <string>
using namespace std;
int main ()
{
cout << "test" << endl;
return 0;
}
# g++ -o demo main.cpp
# ldd demo // 查看依赖的动态链接库文件
linux-vdso.so.1 => (0x00007fffcd1ff000)
libstdc++.so.6 => /usr/lib64/libstdc++.so.6 (0x00007f4d02f69000)
libm.so.6 => /lib64/libm.so.6 (0x00000036c1e00000)
libgcc_s.so.1 => /lib64/libgcc_s.so.1 (0x00000036c7e00000)
libc.so.6 => /lib64/libc.so.6 (0x00000036c1200000)
/lib64/ld-linux-x86-64.so.2 (0x00000036c0e00000)
如果程序引入动态链接库，但没有使用，一样会被链接，且影响启动速度，下面的例子
c++# g++ -o demo -lz -lm -lrt main.cpp // 加入用不到的.so
# ldd demo
linux-vdso.so.1 => (0x00007fff0f7fc000)
libz.so.1 => /lib64/libz.so.1 (0x00000036c2600000)
librt.so.1 => /lib64/librt.so.1 (0x00000036c2200000)
libstdc++.so.6 => /usr/lib64/libstdc++.so.6 (0x00007ff6ab70d000)
libm.so.6 => /lib64/libm.so.6 (0x00000036c1e00000)
libgcc_s.so.1 => /lib64/libgcc_s.so.1 (0x00000036c7e00000)
libc.so.6 => /lib64/libc.so.6 (0x00000036c1200000)
libpthread.so.0 => /lib64/libpthread.so.0 (0x00000036c1a00000)
/lib64/ld-linux-x86-64.so.2 (0x00000036c0e00000)
# ldd -u demo // 查看没有用到的.so
Unused direct dependencies:
/lib64/libz.so.1
/lib64/librt.so.1
/lib64/libm.so.6
/lib64/libgcc_s.so.1
软连接、硬连接
系统中只有一份数据，若一个用户修改，其他用户可以同步感知
硬链接：通过索引节点来进行链接。磁盘中的文件具有的索引编号（Inode）（允许一个文件拥有多个有效路径名）
- 以文件副本的形式存在。但不占用实际空间。
- 不允许给目录创建硬链接。
- 硬链接只有在同一个文件系统中才能创建。
- 删除其中一个硬链接文件并不影响其他有相同 inode 号的文件。
- 不同用户看来文件名可以不同
软连接：（符号连接，快捷方式）软链接就是一个普通文件，存放另一文件的路径
- 软链接是存放另一个文件的路径的形式存在。
- 可以跨文件系统
- 可以对一个不存在的文件名进行链接，硬链接必须要有源文件。
- 可以对目录进行链接。
shell[oracle@Linux]$ touch f1 #创建一个测试文件f1 原有文件
[oracle@Linux]$ ln f1 f2 #创建f1的一个硬连接文件f2 ln 源地址 目标地址
[oracle@Linux]$ ln -s f1 f3 #创建f1的一个符号连接文件f3 ln -s 源地址 目标地址
[oracle@Linux]$ ls -li # -i参数显示文件的inode节点信息
total 0
9797648 -rw-r--r-- 2 oracle oinstall 0 Apr 21 08:11 f1
9797648 -rw-r--r-- 2 oracle oinstall 0 Apr 21 08:11 f2
9797649 lrwxrwxrwx 1 oracle oinstall 2 Apr 21 08:11 f3 -> f1
#硬连接文件 f2 与原文件 f1 的 inode 节点相同，均为 9797648，然而符号连接文件的 inode 节点不同。
shell[oracle@Linux]$ echo "I am f1 file" >>f1
[oracle@Linux]$ cat f1
I am f1 file
[oracle@Linux]$ cat f2
I am f1 file
[oracle@Linux]$ cat f3
I am f1 file
[oracle@Linux]$ rm -f f1
[oracle@Linux]$ cat f2
I am f1 file
[oracle@Linux]$ cat f3
cat: f3: No such file or directory
#当删除原始文件 f1 后，硬连接 f2 不受影响，但是符号连接 f3 文件无效
Linux权限
文件角色有3种：
- 文件拥有者 ：谁创建这文件谁就是拥有者；
- 文件所属组 ：所有用户都要隶属于某一个组，哪怕只有一个人；
- 其他人 ：除了拥有者之外的人都是other。
更改拥有者 ： 需要 sudo 提升到管理员身份才能修改
**更改所属组 ：**sudo chgrp yz func.c
权限数字定义
-
rwx = 4 + 2 + 1 = 7
-
rw = 4 + 2 = 6
-
rx = 4 +1 = 5
即
-
若要同时设置 rwx (可读写运行） 权限则将该权限位 设置 为 4 + 2 + 1 = 7
-
若要同时设置 rw- （可读写不可运行）权限则将该权限位 设置 为 4 + 2 = 6
-
若要同时设置 r-x （可读可运行不可写）权限则将该权限位 设置 为 4 +1 = 5
设备驱动
逻辑设备表
记录了逻辑设备名称与物理设备名称的对应关系以及驱动程序入口地址
字符设备、块设备、网络设备
socket
用户建立一个socket，指明网络协议、端口号等，在内核中开辟一个空间，返回句柄fd
用户将数据包用write系统调用传给内核，内核调用网卡驱动发送出去
对端主机反向处理数据，应用采用read系统调用读取
grep
shellgrep "^a" a.txt ## 查找以a开头的行
grep "^a.*r$" a.txt ## 同时查找以a开头同时以r结尾的行
grep "^a.*h.*r$" a.txt ## 同时查找以a开头，包含字符h，并以r结尾的行
grep "^a\|e$" a.txt ## 提取以a开头，或者以e结尾的行
\ 反义字符：如"\"\""表示匹配""
[ - ] 匹配一个范围，[0-9a-zA-Z]匹配所有数字和字母
* 所有字符，长度可为0
+ 前面的字符出现了一次或者多次
^ #匹配行的开始 如：'^grep'匹配所有以grep开头的行。
$ #匹配行的结束 如：'grep$'匹配所有以grep结尾的行。
. #匹配一个非换行符的字符 如：'gr.p'匹配gr后接一个任意字符，然后是p。
* #匹配零个或多个先前字符 如：'*grep'匹配所有一个或多个空格后紧跟grep的行。
.* #一起用代表任意字符。
[] #匹配一个指定范围内的字符，如'[Gg]rep'匹配Grep和grep。
[^] #匹配一个不在指定范围内的字符，如：'[^A-FH-Z]rep'匹配不包含A-R和T-Z的一个字母开头，紧跟rep的行。
\(..\) #标记匹配字符，如'\(love\)'，love被标记为1。
\< #到匹配正则表达式的行开始，如:'\<grep'匹配包含以grep开头的单词的行。
\> #到匹配正则表达式的行结束，如'grep\>'匹配包含以grep结尾的单词的行。
x\{m\} #重复字符x，m次，如：'0\{5\}'匹配包含5个o的行。
x\{m,\} #重复字符x,至少m次，如：'o\{5,\}'匹配至少有5个o的行。
x\{m,n\} #重复字符x，至少m次，不多于n次，如：'o\{5,10\}'匹配5--10个o的行。
\w #匹配文字和数字字符，也就是[A-Za-z0-9]，如：'G\w*p'匹配以G后跟零个或多个文字或数字字符，然后是p。
\W #\w的反置形式，匹配一个或多个非单词字符，如点号句号等。
\b #单词锁定符，如: '\bgrep\b'只匹配grep。
文件大小写转换
shellcat file | tr a-z A-Z > newfile #将文件内容转换为大写
LInux是否支持浮点运算
Linux kernel默认不支持浮点计算。因为浮点相关寄存器(浮点计算上下文)在系统调用（进程切换）的过程中不会被保存，出于进程切换效率的考虑
Linux的7种文件类型
-
普通文件类型
Linux中最多的一种文件类型, 包括 纯文本文件；二进制文件；数据格式的文件；各种压缩文件。第一个属性为 [-]
-
目录文件
就是目录， 能用 cd 命令进入的。第一个属性为 [d]
-
块设备文件
块设备文件 ： 硬盘。例如一号硬盘的代码是 /dev/hda1等文件。第一个属性为 [b]
-
字符设备
即串行端口的接口设备，例如键盘、鼠标等等。第一个属性为 [c]
-
套接字文件
这类文件通常用在网络数据连接。可以启动一个程序来监听客户端的要求，客户端就可以通过套接字来进行数据通信。第一个属性为 [s]，最常在 /var/run目录中看到这种文件类型
-
管道文件
FIFO也是一种特殊的文件类型，它主要的目的是，解决多个程序同时存取一个文件所造成的错误。第一个属性为 [p]
-
链接文件
类似Windows下面的快捷方式。第一个属性为 [l]
Cortex-M能否运行Linux
不能，其不存在硬件的MMU（内存管理单元）（将硬件物理地址映射到虚拟地址并做检查）
STM32MP1（Cortex-A7）可运行Linux
shell脚本语法与命令
shell#!/bin/bash
echo "Hello World !" # 打印输出
your_name="runoob.com" # 定义变量
1.hello drv
c++#include <linux/mm.h>
#include <linux/module.h>
#include <linux/miscdevice.h>
#include <linux/slab.h>
#include <linux/vmalloc.h>
#include <linux/mman.h>
#include <linux/random.h>
#include <linux/init.h>
#include <linux/raw.h>
#include <linux/tty.h>
#include <linux/capability.h>
#include <linux/ptrace.h>
#include <linux/device.h>
#include <linux/highmem.h>
#include <linux/backing-dev.h>
#include <linux/shmem_fs.h>
#include <linux/splice.h>
#include <linux/pfn.h>
#include <linux/export.h>
#include <linux/io.h>
#include <linux/uio.h>
#include <linux/uaccess.h>
static int major;
static int hello_open (struct inode *node, struct file *filp)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return 0;
}
static ssize_t hello_read (struct file *filp, char __user *buf, size_t size, loff_t *offset)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return size;
}
static ssize_t hello_write(struct file *filp, const char __user *buf, size_t size, loff_t *offset)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return size;
}
static int hello_release (struct inode *node, struct file *filp)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return 0;
}
/* 1. create file_operations */
static const struct file_operations hello_drv = {
.owner = THIS_MODULE,
.read = hello_read,
.write = hello_write,
.open = hello_open,
.release = hello_release,
};
/* 2. register_chrdev */
/* 3. entry function */
static int hello_init(void)
{
major = register_chrdev(0, "100ask_hello", &hello_drv);
return 0;
}
/* 4. exit function */
static void hello_exit(void)
{
unregister_chrdev(major, "100ask_hello");
}
module_init(hello_init);
module_exit(hello_exit);
MODULE_LICENSE("GPL");
2.hello_drv_trans
c++#include "asm/cacheflush.h"
#include <linux/mm.h>
#include <linux/module.h>
#include <linux/miscdevice.h>
#include <linux/slab.h>
#include <linux/vmalloc.h>
#include <linux/mman.h>
#include <linux/random.h>
#include <linux/init.h>
#include <linux/raw.h>
#include <linux/tty.h>
#include <linux/capability.h>
#include <linux/ptrace.h>
#include <linux/device.h>
#include <linux/highmem.h>
#include <linux/backing-dev.h>
#include <linux/shmem_fs.h>
#include <linux/splice.h>
#include <linux/pfn.h>
#include <linux/export.h>
#include <linux/io.h>
#include <linux/uio.h>
#include <linux/uaccess.h>
static struct class *hello_class;
static int major;
static unsigned char hello_buf[100];
static int hello_open (struct inode *node, struct file *filp)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return 0;
}
static ssize_t hello_read (struct file *filp, char __user *buf, size_t size, loff_t *offset)
{
unsigned long len = size > 100 ? 100 : size;
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
copy_to_user(buf, hello_buf, len);
return len;
}
static ssize_t hello_write(struct file *filp, const char __user *buf, size_t size, loff_t *offset)
{
unsigned long len = size > 100 ? 100 : size;
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
copy_from_user(hello_buf, buf, len);
return len;
}
static int hello_release (struct inode *node, struct file *filp)
{
printk("%s %s %d\n", __FILE__, __FUNCTION__, __LINE__);
return 0;
}
/* 1. create file_operations */
static const struct file_operations hello_drv = {
.owner = THIS_MODULE,
.read = hello_read,
.write = hello_write,
.open = hello_open,
.release = hello_release,
};
/* 2. register_chrdev */
/* 3. entry function */
static int hello_init(void)
{
major = register_chrdev(0, "100ask_hello", &hello_drv);
hello_class = class_create(THIS_MODULE, "hello_class");
if (IS_ERR(hello_class)) {
printk("failed to allocate class\n");
return PTR_ERR(hello_class);
}
device_create(hello_class, NULL, MKDEV(major, 0), NULL, "hello"); /* /dev/hello */
return 0;
}
/* 4. exit function */
static void hello_exit(void)
{
device_destroy(hello_class, MKDEV(major, 0));
class_destroy(hello_class);
unregister_chrdev(major, "100ask_hello");
}
module_init(hello_init);
module_exit(hello_exit);
MODULE_LICENSE("GPL");
3template1_gpio_drv
c++#include <linux/module.h>
#include <linux/poll.h>
#include <linux/fs.h>
#include <linux/errno.h>
#include <linux/miscdevice.h>
#include <linux/kernel.h>
#include <linux/major.h>
#include <linux/mutex.h>
#include <linux/proc_fs.h>
#include <linux/seq_file.h>
#include <linux/stat.h>
#include <linux/init.h>
#include <linux/device.h>
#include <linux/tty.h>
#include <linux/kmod.h>
#include <linux/gfp.h>
#include <linux/gpio/consumer.h>
#include <linux/platform_device.h>
#include <linux/of_gpio.h>
#include <linux/of_irq.h>
#include <linux/interrupt.h>
#include <linux/irq.h>
#include <linux/slab.h>
#include <linux/fcntl.h>
#include <linux/timer.h>
struct gpio_desc{
int gpio;
int irq;
char *name;
int key;
struct timer_list key_timer;
} ;
static struct gpio_desc gpios[2] = {
{131, 0, "gpio_100ask_1", },
{132, 0, "gpio_100ask_2", },
};
/* 主设备号 */
static int major = 0;
static struct class *gpio_class;
/* 环形缓冲区 */
#define BUF_LEN 128
static int g_keys[BUF_LEN];
static int r, w;
struct fasync_struct *button_fasync;
#define NEXT_POS(x) ((x+1) % BUF_LEN)
static int is_key_buf_empty(void)
{
return (r == w);
}
static int is_key_buf_full(void)
{
return (r == NEXT_POS(w));
}
static void put_key(int key)
{
if (!is_key_buf_full())
{
g_keys[w] = key;
w = NEXT_POS(w);
}
}
static int get_key(void)
{
int key = 0;
if (!is_key_buf_empty())
{
key = g_keys[r];
r = NEXT_POS(r);
}
return key;
}
static DECLARE_WAIT_QUEUE_HEAD(gpio_wait);
// static void key_timer_expire(struct timer_list *t)
static void key_timer_expire(unsigned long data)
{
/* data ==> gpio */
// struct gpio_desc *gpio_desc = from_timer(gpio_desc, t, key_timer);
struct gpio_desc *gpio_desc = (struct gpio_desc *)data;
int val;
int key;
val = gpio_get_value(gpio_desc->gpio);
//printk("key_timer_expire key %d %d\n", gpio_desc->gpio, val);
key = (gpio_desc->key) | (val<<8);
put_key(key);
wake_up_interruptible(&gpio_wait);
kill_fasync(&button_fasync, SIGIO, POLL_IN);
}
/* 实现对应的open/read/write等函数，填入file_operations结构体 */
static ssize_t gpio_drv_read (struct file *file, char __user *buf, size_t size, loff_t *offset)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
int err;
int key;
if (is_key_buf_empty() && (file->f_flags & O_NONBLOCK))
return -EAGAIN;
wait_event_interruptible(gpio_wait, !is_key_buf_empty());
key = get_key();
err = copy_to_user(buf, &key, 4);
return 4;
}
static ssize_t gpio_drv_write(struct file *file, const char __user *buf, size_t size, loff_t *offset)
{
unsigned char ker_buf[2];
int err;
if (size != 2)
return -EINVAL;
err = copy_from_user(ker_buf, buf, size);
if (ker_buf[0] >= sizeof(gpios)/sizeof(gpios[0]))
return -EINVAL;
gpio_set_value(gpios[ker_buf[0]].gpio, ker_buf[1]);
return 2;
}
static unsigned int gpio_drv_poll(struct file *fp, poll_table * wait)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
poll_wait(fp, &gpio_wait, wait);
return is_key_buf_empty() ? 0 : POLLIN | POLLRDNORM;
}
static int gpio_drv_fasync(int fd, struct file *file, int on)
{
if (fasync_helper(fd, file, on, &button_fasync) >= 0)
return 0;
else
return -EIO;
}
/* 定义自己的file_operations结构体 */
static struct file_operations gpio_key_drv = {
.owner = THIS_MODULE,
.read = gpio_drv_read,
.write = gpio_drv_write,
.poll = gpio_drv_poll,
.fasync = gpio_drv_fasync,
};
static irqreturn_t gpio_key_isr(int irq, void *dev_id)
{
struct gpio_desc *gpio_desc = dev_id;
printk("gpio_key_isr key %d irq happened\n", gpio_desc->gpio);
mod_timer(&gpio_desc->key_timer, jiffies + HZ/5);
return IRQ_HANDLED;
}
/* 在入口函数 */
static int __init gpio_drv_init(void)
{
int err;
int i;
int count = sizeof(gpios)/sizeof(gpios[0]);
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
for (i = 0; i < count; i++)
{
gpios[i].irq = gpio_to_irq(gpios[i].gpio);
setup_timer(&gpios[i].key_timer, key_timer_expire, (unsigned long)&gpios[i]);
//timer_setup(&gpios[i].key_timer, key_timer_expire, 0);
gpios[i].key_timer.expires = ~0;
add_timer(&gpios[i].key_timer);
err = request_irq(gpios[i].irq, gpio_key_isr, IRQF_TRIGGER_RISING | IRQF_TRIGGER_FALLING, "100ask_gpio_key", &gpios[i]);
}
/* 注册file_operations */
major = register_chrdev(0, "100ask_gpio_key", &gpio_key_drv); /* /dev/gpio_desc */
gpio_class = class_create(THIS_MODULE, "100ask_gpio_key_class");
if (IS_ERR(gpio_class)) {
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
unregister_chrdev(major, "100ask_gpio_key");
return PTR_ERR(gpio_class);
}
device_create(gpio_class, NULL, MKDEV(major, 0), NULL, "100ask_gpio"); /* /dev/100ask_gpio */
return err;
}
/* 有入口函数就应该有出口函数：卸载驱动程序时，就会去调用这个出口函数
*/
static void __exit gpio_drv_exit(void)
{
int i;
int count = sizeof(gpios)/sizeof(gpios[0]);
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
device_destroy(gpio_class, MKDEV(major, 0));
class_destroy(gpio_class);
unregister_chrdev(major, "100ask_gpio_key");
for (i = 0; i < count; i++)
{
free_irq(gpios[i].irq, &gpios[i]);
del_timer(&gpios[i].key_timer);
}
}
/* 7. 其他完善：提供设备信息，自动创建设备节点 */
module_init(gpio_drv_init);
module_exit(gpio_drv_exit);
MODULE_LICENSE("GPL");
4template2_platform_dts
c++#include <linux/module.h>
#include <linux/poll.h>
#include <linux/fs.h>
#include <linux/errno.h>
#include <linux/miscdevice.h>
#include <linux/kernel.h>
#include <linux/major.h>
#include <linux/mutex.h>
#include <linux/proc_fs.h>
#include <linux/seq_file.h>
#include <linux/stat.h>
#include <linux/init.h>
#include <linux/device.h>
#include <linux/tty.h>
#include <linux/kmod.h>
#include <linux/gfp.h>
#include <linux/gpio/consumer.h>
#include <linux/platform_device.h>
#include <linux/of_gpio.h>
#include <linux/of_irq.h>
#include <linux/interrupt.h>
#include <linux/irq.h>
#include <linux/slab.h>
#include <linux/fcntl.h>
#include <linux/timer.h>
struct gpio_desc{
int gpio;
int irq;
char name[128];
int key;
struct timer_list key_timer;
} ;
static struct gpio_desc *gpios;
static int count;
/* 主设备号 */
static int major = 0;
static struct class *gpio_class;
/* 环形缓冲区 */
#define BUF_LEN 128
static int g_keys[BUF_LEN];
static int r, w;
struct fasync_struct *button_fasync;
#define NEXT_POS(x) ((x+1) % BUF_LEN)
static int is_key_buf_empty(void)
{
return (r == w);
}
static int is_key_buf_full(void)
{
return (r == NEXT_POS(w));
}
static void put_key(int key)
{
if (!is_key_buf_full())
{
g_keys[w] = key;
w = NEXT_POS(w);
}
}
static int get_key(void)
{
int key = 0;
if (!is_key_buf_empty())
{
key = g_keys[r];
r = NEXT_POS(r);
}
return key;
}
static DECLARE_WAIT_QUEUE_HEAD(gpio_wait);
// static void key_timer_expire(struct timer_list *t)
static void key_timer_expire(unsigned long data)
{
/* data ==> gpio */
// struct gpio_desc *gpio_desc = from_timer(gpio_desc, t, key_timer);
struct gpio_desc *gpio_desc = (struct gpio_desc *)data;
int val;
int key;
val = gpio_get_value(gpio_desc->gpio);
//printk("key_timer_expire key %d %d\n", gpio_desc->gpio, val);
key = (gpio_desc->key) | (val<<8);
put_key(key);
wake_up_interruptible(&gpio_wait);
kill_fasync(&button_fasync, SIGIO, POLL_IN);
}
/* 实现对应的open/read/write等函数，填入file_operations结构体 */
static ssize_t gpio_drv_read (struct file *file, char __user *buf, size_t size, loff_t *offset)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
int err;
int key;
if (is_key_buf_empty() && (file->f_flags & O_NONBLOCK))
return -EAGAIN;
wait_event_interruptible(gpio_wait, !is_key_buf_empty());
key = get_key();
err = copy_to_user(buf, &key, 4);
return 4;
}
static ssize_t gpio_drv_write(struct file *file, const char __user *buf, size_t size, loff_t *offset)
{
unsigned char ker_buf[2];
int err;
if (size != 2)
return -EINVAL;
err = copy_from_user(ker_buf, buf, size);
if (ker_buf[0] >= sizeof(gpios)/sizeof(gpios[0]))
return -EINVAL;
gpio_set_value(gpios[ker_buf[0]].gpio, ker_buf[1]);
return 2;
}
static unsigned int gpio_drv_poll(struct file *fp, poll_table * wait)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
poll_wait(fp, &gpio_wait, wait);
return is_key_buf_empty() ? 0 : POLLIN | POLLRDNORM;
}
static int gpio_drv_fasync(int fd, struct file *file, int on)
{
if (fasync_helper(fd, file, on, &button_fasync) >= 0)
return 0;
else
return -EIO;
}
/* 定义自己的file_operations结构体 */
static struct file_operations gpio_key_drv = {
.owner = THIS_MODULE,
.read = gpio_drv_read,
.write = gpio_drv_write,
.poll = gpio_drv_poll,
.fasync = gpio_drv_fasync,
};
static irqreturn_t gpio_key_isr(int irq, void *dev_id)
{
struct gpio_desc *gpio_desc = dev_id;
printk("gpio_key_isr key %d irq happened\n", gpio_desc->gpio);
mod_timer(&gpio_desc->key_timer, jiffies + HZ/5);
return IRQ_HANDLED;
}
/* 在入口函数 */
static int gpio_drv_probe(struct platform_device *pdev)
{
int err = 0;
int i;
struct device_node *np = pdev->dev.of_node;
struct resource *res;
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
/* 从platfrom_device获得引脚信息
* 1. pdev来自c文件
* 2. pdev来自设备树
*/
if (np)
{
/* pdev来自设备树 : 示例
reg_usb_ltemodule: regulator@1 {
compatible = "100ask,gpiodemo";
gpios = <&gpio5 5 GPIO_ACTIVE_HIGH>, <&gpio5 3 GPIO_ACTIVE_HIGH>;
};
*/
count = of_gpio_count(np);
if (!count)
return -EINVAL;
gpios = kmalloc(count * sizeof(struct gpio_desc), GFP_KERNEL);
for (i = 0; i < count; i++)
{
gpios[i].gpio = of_get_gpio(np, i);
sprintf(gpios[i].name, "%s_pin_%d", np->name, i);
}
}
else
{
/* pdev来自c文件
static struct resource omap16xx_gpio3_resources[] = {
{
.start = 115,
.end = 115,
.flags = IORESOURCE_IRQ,
},
{
.start = 118,
.end = 118,
.flags = IORESOURCE_IRQ,
}, };
*/
count = 0;
while (1)
{
res = platform_get_resource(pdev, IORESOURCE_IRQ, count);
if (res)
{
count++;
}
else
{
break;
}
}
if (!count)
return -EINVAL;
gpios = kmalloc(count * sizeof(struct gpio_desc), GFP_KERNEL);
for (i = 0; i < count; i++)
{
res = platform_get_resource(pdev, IORESOURCE_IRQ, i);
gpios[i].gpio = res->start;
sprintf(gpios[i].name, "%s_pin_%d", pdev->name, i);
}
}
for (i = 0; i < count; i++)
{
gpios[i].irq = gpio_to_irq(gpios[i].gpio);
setup_timer(&gpios[i].key_timer, key_timer_expire, (unsigned long)&gpios[i]);
//timer_setup(&gpios[i].key_timer, key_timer_expire, 0);
gpios[i].key_timer.expires = ~0;
add_timer(&gpios[i].key_timer);
err = request_irq(gpios[i].irq, gpio_key_isr, IRQF_TRIGGER_RISING | IRQF_TRIGGER_FALLING, "100ask_gpio_key", &gpios[i]);
}
/* 注册file_operations */
major = register_chrdev(0, "100ask_gpio_key", &gpio_key_drv); /* /dev/gpio_desc */
gpio_class = class_create(THIS_MODULE, "100ask_gpio_key_class");
if (IS_ERR(gpio_class)) {
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
unregister_chrdev(major, "100ask_gpio_key");
return PTR_ERR(gpio_class);
}
device_create(gpio_class, NULL, MKDEV(major, 0), NULL, "100ask_gpio"); /* /dev/100ask_gpio */
return err;
}
/* 有入口函数就应该有出口函数：卸载驱动程序时，就会去调用这个出口函数
*/
static int gpio_drv_remove(struct platform_device *pdev)
{
int i;
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
device_destroy(gpio_class, MKDEV(major, 0));
class_destroy(gpio_class);
unregister_chrdev(major, "100ask_gpio_key");
for (i = 0; i < count; i++)
{
free_irq(gpios[i].irq, &gpios[i]);
del_timer(&gpios[i].key_timer);
}
return 0;
}
static const struct of_device_id gpio_dt_ids[] = {
{ .compatible = "100ask,gpiodemo", },
{ /* sentinel */ }
};
static struct platform_driver gpio_platform_driver = {
.driver = {
.name = "100ask_gpio_plat_drv",
.of_match_table = gpio_dt_ids,
},
.probe = gpio_drv_probe,
.remove = gpio_drv_remove,
};
static int __init gpio_drv_init(void)
{
/* 注册platform_driver */
return platform_driver_register(&gpio_platform_driver);
}
static void __exit gpio_drv_exit(void)
{
/* 反注册platform_driver */
platform_driver_unregister(&gpio_platform_driver);
}
/* 7. 其他完善：提供设备信息，自动创建设备节点 */
module_init(gpio_drv_init);
module_exit(gpio_drv_exit);
MODULE_LICENSE("GPL");
5template3_i2c
c++
#include "linux/i2c.h"
#include <linux/module.h>
#include <linux/poll.h>
#include <linux/fs.h>
#include <linux/errno.h>
#include <linux/miscdevice.h>
#include <linux/kernel.h>
#include <linux/major.h>
#include <linux/mutex.h>
#include <linux/proc_fs.h>
#include <linux/seq_file.h>
#include <linux/stat.h>
#include <linux/init.h>
#include <linux/device.h>
#include <linux/tty.h>
#include <linux/kmod.h>
#include <linux/gfp.h>
#include <linux/gpio/consumer.h>
#include <linux/platform_device.h>
#include <linux/of_gpio.h>
#include <linux/of_irq.h>
#include <linux/interrupt.h>
#include <linux/irq.h>
#include <linux/slab.h>
#include <linux/fcntl.h>
#include <linux/timer.h>
/* 主设备号 */
static int major = 0;
static struct class *my_i2c_class;
struct i2c_client *g_client;
static DECLARE_WAIT_QUEUE_HEAD(gpio_wait);
struct fasync_struct *i2c_fasync;
/* 实现对应的open/read/write等函数，填入file_operations结构体 */
static ssize_t i2c_drv_read (struct file *file, char __user *buf, size_t size, loff_t *offset)
{
int err;
struct i2c_msg msgs[2];
/* 初始化i2c_msg */
err = i2c_transfer(g_client->adapter, msgs, 2);
/* copy_to_user */
return 0;
}
static ssize_t i2c_drv_write(struct file *file, const char __user *buf, size_t size, loff_t *offset)
{
int err;
/* copy_from_user */
struct i2c_msg msgs[2];
/* 初始化i2c_msg */
err = i2c_transfer(g_client->adapter, msgs, 2);
return 0;
}
static unsigned int i2c_drv_poll(struct file *fp, poll_table * wait)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
poll_wait(fp, &gpio_wait, wait);
//return is_key_buf_empty() ? 0 : POLLIN | POLLRDNORM;
return 0;
}
static int i2c_drv_fasync(int fd, struct file *file, int on)
{
if (fasync_helper(fd, file, on, &i2c_fasync) >= 0)
return 0;
else
return -EIO;
}
/* 定义自己的file_operations结构体 */
static struct file_operations i2c_drv_fops = {
.owner = THIS_MODULE,
.read = i2c_drv_read,
.write = i2c_drv_write,
.poll = i2c_drv_poll,
.fasync = i2c_drv_fasync,
};
static int i2c_drv_probe(struct i2c_client *client,
const struct i2c_device_id *id)
{
// struct device_node *np = client->dev.of_node;
// struct i2c_adapter *adapter = client->adapter;
/* 记录client */
g_client = client;
/* 注册字符设备 */
/* 注册file_operations */
major = register_chrdev(0, "100ask_i2c", &i2c_drv_fops); /* /dev/gpio_desc */
my_i2c_class = class_create(THIS_MODULE, "100ask_i2c_class");
if (IS_ERR(my_i2c_class)) {
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
unregister_chrdev(major, "100ask_i2c");
return PTR_ERR(my_i2c_class);
}
device_create(my_i2c_class, NULL, MKDEV(major, 0), NULL, "myi2c"); /* /dev/myi2c */
return 0;
}
static int i2c_drv_remove(struct i2c_client *client)
{
/* 反注册字符设备 */
device_destroy(my_i2c_class, MKDEV(major, 0));
class_destroy(my_i2c_class);
unregister_chrdev(major, "100ask_i2c");
return 0;
}
static const struct of_device_id myi2c_dt_match[] = {
{ .compatible = "100ask,i2cdev" },
{},
};
static struct i2c_driver my_i2c_driver = {
.driver = {
.name = "100ask_i2c_drv",
.owner = THIS_MODULE,
.of_match_table = myi2c_dt_match,
},
.probe = i2c_drv_probe,
.remove = i2c_drv_remove,
};
static int __init i2c_drv_init(void)
{
/* 注册i2c_driver */
return i2c_add_driver(&my_i2c_driver);
}
static void __exit i2c_drv_exit(void)
{
/* 反注册i2c_driver */
i2c_del_driver(&my_i2c_driver);
}
/* 7. 其他完善：提供设备信息，自动创建设备节点 */
module_init(i2c_drv_init);
module_exit(i2c_drv_exit);
MODULE_LICENSE("GPL");
6template3_spi
c++#include <linux/spi/spi.h>
#include <linux/module.h>
#include <linux/poll.h>
#include <linux/fs.h>
#include <linux/errno.h>
#include <linux/miscdevice.h>
#include <linux/kernel.h>
#include <linux/major.h>
#include <linux/mutex.h>
#include <linux/proc_fs.h>
#include <linux/seq_file.h>
#include <linux/stat.h>
#include <linux/init.h>
#include <linux/device.h>
#include <linux/tty.h>
#include <linux/kmod.h>
#include <linux/gfp.h>
#include <linux/gpio/consumer.h>
#include <linux/platform_device.h>
#include <linux/of_gpio.h>
#include <linux/of_irq.h>
#include <linux/interrupt.h>
#include <linux/irq.h>
#include <linux/slab.h>
#include <linux/fcntl.h>
#include <linux/timer.h>
/* 主设备号 */
static int major = 0;
static struct class *my_spi_class;
static struct spi_device *g_spi;
static DECLARE_WAIT_QUEUE_HEAD(gpio_wait);
struct fasync_struct *spi_fasync;
/* 实现对应的open/read/write等函数，填入file_operations结构体 */
static ssize_t spi_drv_read (struct file *file, char __user *buf, size_t size, loff_t *offset)
{
// int err;
// struct spi_transfer msgs[2];
/* 初始化 spi_transfer */
// static inline int
// spi_sync_transfer(struct spi_device *spi, struct spi_transfer *xfers,
// unsigned int num_xfers);
/* copy_to_user */
return 0;
}
static ssize_t spi_drv_write(struct file *file, const char __user *buf, size_t size, loff_t *offset)
{
//int err;
/* copy_from_user */
// struct spi_transfer msgs[2];
/* 初始化 spi_transfer */
// static inline int
// spi_sync_transfer(struct spi_device *spi, struct spi_transfer *xfers,
// unsigned int num_xfers);
return 0;
}
static unsigned int spi_drv_poll(struct file *fp, poll_table * wait)
{
//printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
poll_wait(fp, &gpio_wait, wait);
//return is_key_buf_empty() ? 0 : POLLIN | POLLRDNORM;
return 0;
}
static int spi_drv_fasync(int fd, struct file *file, int on)
{
if (fasync_helper(fd, file, on, &spi_fasync) >= 0)
return 0;
else
return -EIO;
}
/* 定义自己的file_operations结构体 */
static struct file_operations spi_drv_fops = {
.owner = THIS_MODULE,
.read = spi_drv_read,
.write = spi_drv_write,
.poll = spi_drv_poll,
.fasync = spi_drv_fasync,
};
static int spi_drv_probe(struct spi_device *spi)
{
// struct device_node *np = client->dev.of_node;
/* 记录spi_device */
g_spi = spi;
/* 注册字符设备 */
/* 注册file_operations */
major = register_chrdev(0, "100ask_spi", &spi_drv_fops); /* /dev/gpio_desc */
my_spi_class = class_create(THIS_MODULE, "100ask_spi_class");
if (IS_ERR(my_spi_class)) {
printk("%s %s line %d\n", __FILE__, __FUNCTION__, __LINE__);
unregister_chrdev(major, "100ask_spi");
return PTR_ERR(my_spi_class);
}
device_create(my_spi_class, NULL, MKDEV(major, 0), NULL, "myspi"); /* /dev/myspi */
return 0;
}
static int spi_drv_remove(struct spi_device *spi)
{
/* 反注册字符设备 */
device_destroy(my_spi_class, MKDEV(major, 0));
class_destroy(my_spi_class);
unregister_chrdev(major, "100ask_spi");
return 0;
}
static const struct of_device_id myspi_dt_match[] = {
{ .compatible = "100ask,spidev" },
{},
};
static struct spi_driver my_spi_driver = {
.driver = {
.name = "100ask_spi_drv",
.owner = THIS_MODULE,
.of_match_table = myspi_dt_match,
},
.probe = spi_drv_probe,
.remove = spi_drv_remove,
};
static int __init spi_drv_init(void)
{
/* 注册spi_driver */
return spi_register_driver(&my_spi_driver);
}
static void __exit spi_drv_exit(void)
{
/* 反注册spi_driver */
spi_unregister_driver(&my_spi_driver);
}
/* 7. 其他完善：提供设备信息，自动创建设备节点 */
module_init(spi_drv_init);
module_exit(spi_drv_exit);
MODULE_LICENSE("GPL");
