目录
嵌入式软件开发工程师
1.数据结构
数组、链表、栈、队列、树(二叉搜索树)、图
2.算法核心
1.链表
1.1 反转链表
C++/**
* 迭代法实现反转列表
* @param head ListNode类
* @return ListNode类
*/
struct ListNode* ReverseList(struct ListNode* head ) {
// write code here
struct ListNode *Current,*Prev,*next;
Current = head;
Prev = NULL;
while(Current != NULL){
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head = Prev;
return head;
}
1.2 反转指定区间内得链表比如1->2->3->4->5->NULL,m=2,n=3;返回1->4->3->2->5->NULL
C++/**
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
struct ListNode* reverseBetween(struct ListNode* head, int m, int n ) {
// write code here
if(head == NULL)return head;
if(head->next == NULL)return head;
if(m == n)return head;
struct ListNode *Current,*Prev,*next,*start,*start_last;
int i;
Current = head;
Prev = NULL;
next = NULL;
// 先找到开始位置
for (i=1; i<m; i++) {
next = Current->next;
// Current->next = Prev;
Prev = Current;
Current = next;
}
// 标记
start_last = Prev;
start = Current;
// 反转
for (i=0; i<(n-m+1); i++) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
// 头尾节点重指向
if(start != head){
start->next = next;
start_last->next = Prev;//start!=head的情况下,需要保留start上一个指针
}
else {
start->next = next;
head = Prev;//start==head的情况下,直接将head指向待反转的最后一个
}
return head;
}
1.3 输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
C++/**
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
struct ListNode* Merge(struct ListNode* pHead1, struct ListNode* pHead2 ) {
// write code here
if(pHead1 == NULL)return pHead2;
if(pHead2 == NULL)return pHead1;
struct ListNode* p1 = (pHead1->val <= pHead2->val ? pHead1 : pHead2);
struct ListNode* p2 = (pHead1->val > pHead2->val ? pHead1 : pHead2);
struct ListNode* p = p1; //p1是主链
// temp存放中间指针,有可能在p1中有可能在p2中,最终每次指向p1链两个node之间和大node最近的那个点
struct ListNode* temp =NULL;
while((p1 != NULL)&&(p2 != NULL)){
if(p1->val <= p2->val){
temp = p1;
p1 = p1->next;
}
else {
temp->next = p2;
temp = p2;
p2 = p2->next;
temp->next = p1;
}
}
if(p1 == NULL){
temp->next =p2;
return p;
}else return p;
}
1.4 合并K个递增的链表,单个链表的长度为n,合并这k链表并使新链表中的节点仍然是递增排序的。 方法一:先将数值存放在一个数组中,排序,再给链表赋新值
C++/**
* @param lists ListNode类一维数组
* @param listsLen int lists数组长度
* @return ListNode类
*/
struct ListNode* mergeKLists(struct ListNode** lists, int listsLen ) {
// write code here
int i=0;
struct ListNode* pHead1 = NULL;
// 找到列表中第一个非空链表
for(i=0;i<listsLen;i++){
if(lists[i] == NULL)continue;
else{
pHead1 = lists[i];//找到后跳出
break;
}
}
// 如果没找到,则列表中全是空的链表,直接返回NULL
if(pHead1 == NULL)return pHead1;
// 接下来进行两个链表的合并
for(i=i+1;i<listsLen;i++){
struct ListNode* pHead2 = lists[i];
if(pHead2 == NULL)continue;
struct ListNode* p1 = (pHead1->val <= pHead2->val ? pHead1 : pHead2);
struct ListNode* p2 = (pHead1->val > pHead2->val ? pHead1 : pHead2);
struct ListNode* p = p1; //p1是主链
// temp存放中间指针,有可能在p1中有可能在p2中,最终每次指向p1链两个node之间和大node最近的那个点
struct ListNode* temp =NULL;
while((p1 != NULL)&&(p2 != NULL)){
if(p1->val <= p2->val){
temp = p1;
p1 = p1->next;
}
else {
temp->next = p2;
temp = p2;
p2 = p2->next;
temp->next = p1;
}
}
// 使用pHead1指向合并的俩链表
if(p1 == NULL){
temp->next =p2;
pHead1 = p;
}else pHead1 = p;
}
return pHead1;
}
方法二、使用自底向上的方法实现归并排序,则可以达到O(nlogn)的时间复杂度、O(1)的空间复杂度。首先求得链表的长度 length,然后将链表拆分成子链表进行合并。
具体做法如下。
- 用 subLength表示每次需要排序的子链表的长度,初始时 subLength=1。
- 每次将链表拆分成若干个长度为 subLength的子链表(最后一个子链表的长度可以小于 subLength,按照每两个子链表一组进行合并,合并后即可得到若干个长度为 subLength×2的有序子链表(最后一个子链表的长度可以小于 subLength×2。合并两个子链表仍然使用「21. 合并两个有序链表」的做法。
- 将 subLength的值加倍,重复第 2 步,对更长的有序子链表进行合并操作,直到有序子链表的长度大于或等于 length,整个链表排序完毕。
C++/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head == nullptr)return head;
int length = 0;
ListNode *node = head;
while(node != nullptr){
length++;
node = node->next;
}
ListNode* dummyHead = new ListNode(0, head);
for(int subLength = 1; subLength < length; subLength <<= 1){
ListNode *pre = dummyHead, *cur = dummyHead->next;
while(cur != nullptr){
ListNode *head1 = cur;
for(int i = 1; i < subLength && cur->next != nullptr; i++){
cur = cur->next;
}
ListNode *head2 = cur->next;
cur->next = nullptr;
cur = head2;
for(int i = 1; i < subLength && cur != nullptr && cur->next != nullptr;i++){
cur = cur->next;
}
ListNode* next = nullptr;
if(cur != nullptr){
next = cur->next;
cur->next = nullptr;
}
ListNode *merged = merge(head1, head2);
pre->next = merged;
while(pre->next != nullptr){
pre = pre->next;
}
cur = next;
}
}
return dummyHead->next;
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
1.5 判断链表中是否有环,思想:使用快慢指针fast和slow,fast 指针每次向后移动两个位置,而slow 指针每次向后移动一个位置。如果链表中存在环,则 fast 指针最终将再次与 slow 指针在环中相遇。
C++/**
* @param head ListNode类
* @return bool布尔型
*/
bool hasCycle(struct ListNode* head ) {
// write code here
//快慢指针
struct ListNode* fast = head;
struct ListNode* slow = head;
while (fast != NULL && slow != NULL) {
if (fast->next != NULL) {
fast = fast->next->next; //快指针每次2步
} else {
return false;
}
slow = slow->next; //慢指针每次1步
if (fast == slow) {
return true;
}
}
return false;
}
1.6 给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。
C++/**
*方法一、使用C语言快慢指针
* @param pHead ListNode类
* @return ListNode类
*/
struct ListNode* EntryNodeOfLoop(struct ListNode* pHead ) {
// write code here
// 方法一、快慢指针
struct ListNode *fast = pHead,*slow = pHead;// 快慢指针一开始都指向头
while(fast){
slow =slow->next; // 慢指针走一步
if(fast->next == NULL)return NULL;// 若快指针的下一步不能走,则说明两指针不会相遇
fast = fast->next->next;// 快指针向后走两步
if(fast == slow){// 找到相交节点, 此时慢指针已经走了nb步
fast = pHead;// 快指针重新移动到头
while(fast != slow){// 直到两指针相遇位置,每次向后走一步
fast = fast->next;
slow = slow->next;
}
return fast;// 找到入口节点,直接返回
}
}
return NULL;
}
/*
*方法二、使用C++语言 哈希表
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
unordered_set<ListNode*> st; // 哈希集合
while(pHead){
if(st.count(pHead)) return pHead; // 若已经记录过,直接返回
st.insert(pHead); // 记录当前结点
pHead = pHead->next;
}
return nullptr; // 无环
}
};
1.7 链表中倒数最后k个结点
C++/**
* @param pHead ListNode类
* @param k int整型
* @return ListNode类
*/
struct ListNode* FindKthToTail(struct ListNode* pHead, int k ) {
// write code here
struct ListNode* Current;
int i = 0, j =0;
Current = pHead;
while (Current != NULL) {
i++;
Current = Current->next;
}
if(i < k)return NULL;
else {
for(j=0;j<(i-k);j++){
pHead = pHead->next;
}
}
return pHead;
}
1.8 输入两个无环的单向链表,找出它们的第一个公共结点,如果没有公共节点则返回空。
C++/*
*方法一:使用C++语言 哈希表
*方法二、使用两个指针分别指向两个链表,其中一个指针走完链表1走链表2,另外一个类似,如果有共同节点,那么最后一起到达末尾,所以第一次相遇的地方就是入口公告节点,如果最后都等于空的话则没有公共节点。
*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
unordered_set<ListNode*> st; // 哈希集合
while(pHead1){
st.insert(pHead1);
pHead1 = pHead1->next;
}
while(pHead2){
if(st.count(pHead2)) return pHead2; // 若已经记录过,直接返回
pHead2 = pHead2->next;
}
return nullptr; // 无环
}
};
1.9 两个链表相加

C++/**
* @param head1 ListNode类
* @param head2 ListNode类
* @return ListNode类
*/
#include <stdlib.h>
struct ListNode* addInList(struct ListNode* head1, struct ListNode* head2 ) {
// write code here
struct ListNode* Current, *Prev, *next;
int i = 0;
//反转链表1
Current = head1;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head1 = Prev;
//反转链表2
Current = head2;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head2 = Prev;
//直接相加
Current = head1;
while (Current) {
Current->val = Current->val + head2->val;
if ((Current->next == NULL) && (head2->next == NULL))break;
else {
if (Current->next == NULL) {
Current->next = head2->next;
break;
}
if (head2->next == NULL) {
break;
}
}
Current = Current->next;
head2 = head2->next;
}
//判断相加后的链表节点值是否大于10,更正
Current = head1;
while(Current){
if(i == 1){
if(Current->val + 1 >= 10){
Current->val = Current->val + 1 - 10;
i = 1;
}
else {
Current->val = Current->val + 1;
i = 0;
}
}
else {
if(Current->val >= 10){
Current->val = Current->val - 10;
i = 1;
}
else {
i = 0;
}
}
Current = Current->next;
}
//再反转
Current = head1;
Prev = NULL;
while (Current != NULL) {
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head1 = Prev;
// 判断第一个值(反转前最后一个值)是否大于10,如果大于则创建一个新的节点
if (i == 1) {
struct ListNode* temp = (struct ListNode*)malloc(sizeof(struct ListNode));
temp->val = 1;
temp->next = head1;
head1 = temp;
}
return head1;
}
1.10 单链表排序
C++/**
* @param head ListNode类 the head node
* @return ListNode类
*/
#include <stdio.h>
struct ListNode* sortInList(struct ListNode* head ) {
// write code here
int NodeVal[100000];
int i = 0;
int len = 0;
int j, temp;
struct ListNode* current = head;
//将链表中的值保存在数组
while (current) {
NodeVal[i] = current->val;
current = current->next;
i++;
}
len = i;
//冒泡排序算法:进行 n-1 轮比较
for (i = 0; i < len - 1; i++) {
//每一轮比较前 n-1-i 个,也就是说,已经排序好的最后 i 个不用比较
for (j = 0; j < len - 1 - i; j++) {
if (NodeVal[j] > NodeVal[j + 1]) {
temp = NodeVal[j];
NodeVal[j] = NodeVal[j + 1];
NodeVal[j + 1] = temp;
}
}
}
//将排序好的数组赋值到链表
i = 0;
current = head;
while (current){
current->val = NodeVal[i++];
current = current->next;
}
return head;
}
1.11 判断一个链表是否为回文结构(即前序 后序遍历一样)
C++/**
* @param head ListNode类 the head
* @return bool布尔型
*/
#include <stdbool.h>
bool isPail(struct ListNode* head ) {
// write code here
struct ListNode *Current,*Prev,*next;
//定义数组存入前序值
int aa[100000];
int i = 0;
Current = head;
while(Current){
aa[i++] = Current->val;
Current = Current->next;
}
// 链表反转
Current = head;
Prev = NULL;
while(Current != NULL){
next = Current->next;
Current->next = Prev;
Prev = Current;
Current = next;
}
head = Prev;
//对比
Current = head;
i = 0;
while(Current){
if(Current->val == aa[i++]){
Current = Current->next;
}
else{
return false;
}
}
return true;
}
1.12 链表的奇偶重排:先奇节点再偶节点如输入1->2->3->4->5->6->null,输出1->3->5->2->4->6->null.
C++/**
* @param head ListNode类
* @return ListNode类
*/
struct ListNode* oddEvenList(struct ListNode* head ) {
// write code here
if(head == NULL)return head;
if(head->next == NULL)return head;
struct ListNode *cur,*forw,*forw1;
cur = head;
forw = forw1 = head->next;
// 奇偶节点跳跳乐
while(cur){
if(cur->next != NULL){
if(cur->next->next != NULL){
cur->next = cur->next->next;
cur = cur->next;
}
else break;
}
else break;
if(forw->next != NULL){
if(forw->next->next != NULL){
forw->next = forw->next->next;
forw = forw->next;
}
}
}
// 当奇数个节点的时候偶数跳跃最后不指向空
if(forw->next != NULL)forw->next = NULL;
// 指向第一个偶节点
cur->next = forw1;
return head;
}
1.13 删除有序链表中重复的元素,删除给出链表中的重复元素(链表中元素从小到大有序),使链表中的所有元素都只出现一次
C++/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param head ListNode类
* @return ListNode类
*/
ListNode* deleteDuplicates(ListNode* head) {
// write code here
if(head == nullptr)return head;
struct ListNode *cur = head,*last = head,*temp;
cur = cur->next;
while (last&&cur) {
if(last->val == cur->val){
// last->next = cur->next;
// last = last->next;
temp = cur;
cur = cur->next;
temp = nullptr;
delete temp;
last->next = cur;
}
else{
cur = cur->next;
last = last->next;
}
}
return head;
}
};
1.14 删除有序链表中重复的元素,给出一个升序排序的链表,删除链表中的所有重复出现的元素,只保留原链表中只出现一次的元素。
C++/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param head ListNode类
* @return ListNode类
*/
ListNode* deleteDuplicates(ListNode* head) {
// write code here
if (head == nullptr)return nullptr;
ListNode* res = new ListNode(0);//在链表前加一个表头
res->next = head;
ListNode* cur = res;
while (cur->next != nullptr && cur->next->next != nullptr) {
//遇到相邻两个节点值相同
if (cur->next->val == cur->next->next->val) {
int temp = cur->next->val;
//将所有相同的都跳过
while (cur->next != nullptr && cur->next->val == temp)
cur->next = cur->next->next;
} else
cur = cur->next;
}
//返回时去掉表头
return res->next;
}
};
2.二分查找/排序
2.1 二分查找
C++class Solution {
public:
/**
* @param nums int整型vector
* @param target int整型
* @return int整型
*/
int search(vector<int>& nums, int target) {
// write code here
int left = 0;
int right = nums.size() - 1;
while(left <= right){
int mid = left + (right - left)/2;
if(nums[mid] == target)return mid;
if(nums[mid] < target){
left = mid + 1;
}
else{
right = mid - 1;
}
}
return -1;
}
};
2.2 寻找峰值
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int findPeakElement(vector<int>& nums) {
// write code here
int left = 0;
int right = nums.size() - 1;
// 二分法
while(left < right){
int mid = (left + right) / 2;
//右边是往下,不一定有坡峰
if(nums[mid] > nums[mid+1]){
right = mid;
}
//右边是往上,一定能找到波峰
else {
left = mid + 1;
}
}
return right;
}
};
2.3 数组中逆序对 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007 思路:在归并排序过程中,局部有序后,如果一个局部有序的最小值大于另一个局部有序的最大值,那么第一个局部有序后面的值与都可以与第二个局部有序的值构成逆序对,简化了计算时间。
C++class Solution {
private:
const int kmod = 1000000007;
public:
/**
* @param nums int整型vector
* @return int整型
*/
int InversePairs(vector<int>& nums) {
// write code here
int ret = 0;
// 在最外层开辟数组
vector<int> tmp(nums.size());
merge_sort__(nums, tmp, 0, nums.size() - 1, ret);
return ret;
}
void merge_sort__(vector<int>& arr, vector<int>& tmp, int l, int r, int& ret) {
if (l >= r) {
return;
}
int mid = l + ((r - l) >> 1);
merge_sort__(arr, tmp, l, mid, ret);
merge_sort__(arr, tmp, mid + 1, r, ret);
merge__(arr, tmp, l, mid, r, ret);
}
void merge__(vector<int>& arr, vector<int>& tmp, int l, int mid, int r, int& ret) {
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (arr[i] > arr[j]) {
tmp[k++] = arr[j++];
ret += (mid - i + 1);
ret %= kmod;
} else {
tmp[k++] = arr[i++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= r) {
tmp[k++] = arr[j++];
}
for (k = 0, i = l; i <= r; ++i, ++k) {
arr[i] = tmp[k];
}
}
};
2.4 求旋转数组的最小数字,有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int minNumberInRotateArray(vector<int>& nums) {
// write code here
int left = 0;
int right = nums.size() - 1;
while(left < right){
int mid = (left + right) / 2;
//最小的数字在mid右边
if(nums[mid] > nums[right]){
left = mid + 1;
}
// 无法判断,一个一个试
else if(nums[mid] == nums[right]) {
right-- ;
}
else {
right = mid;
}
}
return nums[left];
}
};
2.5 你2个版本号version1和version2,请你比较他们的大小。版本号是由修订号组成,修订号与修订号之间由一个"."连接。1个修订号可能有多位数字组成,修订号可能包含前导0,且是合法的。例如,1.02.11,0.1,0.2都是合法的版本号。每个版本号至少包含1个修订号。 修订号从左到右编号,下标从0开始,最左边的修订号下标为0,下一个修订号下标为1,以此类推。
C++#include <iostream>
#include <ostream>
#include <string>
class Solution {
public:
/**
* 比较版本号
* @param version1 string字符串
* @param version2 string字符串
* @return int整型
*/
int compare(string version1, string version2) {
// write code here
int n1 = version1.size();
int n2 = version2.size();
int i = 0, j = 0;
while (i < n1 || j < n2) {
long long num1 = 0;
while (i < n1 && version1[i] != '.') {
num1 = num1 * 10 + version1[i] - '0';
i++;
}
i++;//跳过点
long long num2 = 0;
while (j < n2 && version2[j] != '.') {
num2 = num2 * 10 + version2[j] - '0';
j++;
}
j++;//跳过点
if(num1 > num2)return 1;
if(num1 < num2)return -1;
}
return 0;
}
};
3.二叉树
3.1 二叉树的前序遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Preorder(vector<int> &res, TreeNode* root) {
if (root == nullptr) return;
res.push_back(root->val);
Preorder(res,root->left);
Preorder(res,root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Preorder(result, root);
return result;
}
};
3.2 二叉树的中序遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Inorder(vector<int>&result, TreeNode* root){
if(root == nullptr)return;
Inorder(result, root->left);
result.push_back(root->val);
Inorder(result, root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Inorder(result, root);
return result;
}
};
3.3 二叉树的后续遍历
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型vector
*/
void Postorder(vector<int> &result, TreeNode* root){
if(root == nullptr)return;
Postorder(result, root->left);
Postorder(result, root->right);
result.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
// write code here
vector<int> result;
Postorder(result, root);
return result;
}
};
3.4 二叉树的最大深度,此时定义深度是指树的根节点到任一叶子节点路径上节点的数量。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param root TreeNode类
* @return int整型
*/
int maxDepth(TreeNode* root) {
// write code here
int LeftHeight = 0;
int RightHeight = 0;
if (root == nullptr) {
return 0;
}
LeftHeight = maxDepth(root->left);
RightHeight = maxDepth(root->right);
if (LeftHeight >= RightHeight)return LeftHeight + 1;
else return RightHeight + 1;
}
};
3.5 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点
C++//方法一 将中序遍历的结果用数组存储下来,得到的数组是有从小到大顺序的。最后将数组中的结点依次连接即可。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<TreeNode*> TreeList;//定义一个数组,根据中序遍历来存储结点。
void inorder(TreeNode* root) {
if (!root) return;
inorder(root->left);
TreeList.push_back(root);
inorder(root->right);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
inorder(pRootOfTree);
for (int i = 0; i < TreeList.size() - 1; i++) { //根据数组中的顺序将结点连接,注意i的范围。
TreeList[i]->right = TreeList[i + 1];
TreeList[i + 1]->left = TreeList[i];
}
return TreeList[0];//数组的头部存储的是双向链表的第一个结点。
}
};
//方法二 根据题目的要求1,不能创建新的结点,而方法一的数组中存储的其实是结点,并不满足题意;所以需要在中序遍历的过程中,直接对结点的指针进行调整。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* preNode;//preNode一定是全局变量。
void inorder(TreeNode* root) {
if (!root) return;
inorder(root->left);
//当前结点中需要进校的调整。
root->left = preNode;
if (preNode) {
preNode->right = root;
}
preNode = root;//更新preNode,指向当前结点,作为下一个结点的前继。
inorder(root->right);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
TreeNode* p = pRootOfTree;
while (p->left) p = p->left;//找到双向链表的开头。
inorder(pRootOfTree);
return p;
}
};
3.6 合并两个二叉树,合并规则是:都存在的结点,就将结点值加起来,否则空的位置就由另一个树的结点来代替。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param t1 TreeNode类
* @param t2 TreeNode类
* @return TreeNode类
*/
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
// write code here
if(t1 == nullptr)return t2;
if(t2 == nullptr)return t1;
TreeNode* head = new TreeNode(t1->val + t2->val);
head->left = mergeTrees(t1->left, t2->left);
head->right = mergeTrees(t1->right, t2->right);
return head;
}
};
3.7 二叉树的镜像,镜像的概念是父节点的左右子节点(及其子孙)交换
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot) {
// write code here
if(pRoot == nullptr)return pRoot;
TreeNode *temp = new TreeNode(0);
temp->left = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = temp->left;
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
}
};
3.8 判断是不是二叉搜索树
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param root TreeNode类
* @return bool布尔型
*/
bool IsSubtreeLesser(struct TreeNode* root, int data) {
if (root == nullptr)return true;
if (root->val <= data
&& IsSubtreeLesser(root->left, data)
&& IsSubtreeLesser(root->right, data))
return true;
else
return false;
}
bool IsSubtreeGreater(struct TreeNode* root, int data) {
if (root == nullptr)return true;
if (root->val >= data
&& IsSubtreeGreater(root->left, data)
&& IsSubtreeGreater(root->right, data))
return true;
else
return false;
}
bool isValidBST(TreeNode* root) {
// write code here
if (root == nullptr)return true;
if (IsSubtreeLesser(root->left, root->val)
&& IsSubtreeGreater(root->right, root->val)
&& isValidBST(root->left)
&& isValidBST(root->right))
return true;
else
return false;
}
};
3.9 判断是不是完全二叉树,若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <queue>
class Solution {
public:
/**
* @param root TreeNode类
* @return bool布尔型
*/
bool isCompleteTree(TreeNode* root) {
// write code here
if(root == nullptr)return true;
queue<TreeNode*> q;
q.push(root);
bool flag = false;
//层次遍历
while(!q.empty()){
int sz = q.size();
for(int i = 0; i < sz; i++){
TreeNode* cur = q.front();
q.pop();
//标记第一次遇到空节点
if(cur == nullptr)flag = true;
else {
//后续访问已经遇到空节点了,说明经过了叶子
if(flag)return false;
q.push(cur->left);
q.push(cur->right);
}
}
}
return true;
}
};
3.10 输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树,具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <cstdio>
class Solution {
public:
/**
* @param pRoot TreeNode类
* @return bool布尔型
*/
int maxDepth(TreeNode* root) {
// write code here
int LeftHeight = 0;
int RightHeight = 0;
if (root == nullptr) {
return -1;
}
LeftHeight = maxDepth(root->left);
RightHeight = maxDepth(root->right);
if (LeftHeight >= RightHeight)return LeftHeight + 1;
else return RightHeight + 1;
}
bool IsBalanced_Solution(TreeNode* pRoot) {
// write code here
if(pRoot == nullptr)return true;
int left_h = maxDepth(pRoot->left);
int right_h = maxDepth(pRoot->right);
printf("%d,%d",left_h,right_h);
if((abs(left_h - right_h) <= 1)
&&IsBalanced_Solution(pRoot->left)
&&IsBalanced_Solution(pRoot->right))return true;
else return false;
}
};
3.11 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <cstdio>
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @param p int整型
* @param q int整型
* @return int整型
*/
vector<int> Path(TreeNode* root, int a) {
vector<int> path_v;
TreeNode* temp = root;
while (temp->val != a) {
if (temp->val != a) {
path_v.push_back(temp->val);
}
if (temp->val < a)temp = temp->right;
else temp = temp->left;
}
path_v.push_back(temp->val);
return path_v;
}
int lowestCommonAncestor(TreeNode* root, int p, int q) {
// write code here
// p路径 q路径(包含自身)
vector<int> path_p = Path(root, p);
vector<int> path_q = Path(root, q);
int res;
// 比较两个路径
for (int i = 0; i < min(path_p.size(), path_q.size()); i++) {
if(path_p[i] == path_q[i]){
// 最后一个相同的节点就是最近的公共祖先
res = path_p[i];
}
}
return res;
}
};
3.12 给定一个二叉树,找到指定节点的最近公共祖先(用到了深度搜索,递归方法)
如果返回的是节点值那么路径就定义为vector<int>,如果要返回的是节点就定义为:vector<TreeNode*>;
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <vector>
class Solution {
public:
/**
* @param root TreeNode类
* @param o1 int整型
* @param o2 int整型
* @return int整型
*/
bool find = false;
void dfs(vector<int>&path, TreeNode* root, int o){
if(find || root == nullptr)return;//已经找到或者到达空节点
path.push_back(root->val);
if(root->val == o){
find = true;
return;
}
dfs(path, root->left, o);
dfs(path, root->right, o);
if(find)return;//防止去除节点
path.pop_back();//不在这条路径上,去除节点
}
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
// write code here
vector<int> path1, path2;
dfs(path1, root, o1);
find = false;
dfs(path2, root, o2);
int res;
for(int i = 0; i < min(path1.size(),path2.size()); i++){
if(path1[i] == path2[i])res = path1[i];
}
return res;
}
};
3.13 序列化和反序列化二叉树,二叉树的序列化(Serialize)是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串。
C++/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
//处理序列化的功能函数(递归)
void SerializeFunction(TreeNode* root, string& str) {
// 如果指针为空,表示左叶子节点或右叶子节点为空,用#表示
if (root == nullptr) {
str += '#';
return;
}
// 根节点
string temp = to_string(root->val);
str += temp + '!';//加!区分节点
// 左右子树
SerializeFunction(root->left, str);
SerializeFunction(root->right, str);
}
char* Serialize(TreeNode* root) {
// 处理空树
if (root == nullptr)return "#";
string res;
SerializeFunction(root, res);
// 把str转换成char
char* charRes = new char[res.length() + 1];
strcpy(charRes, res.c_str());
charRes[res.length()] = '\0';
return charRes;
}
//处理反序列化的功能函数(递归)
TreeNode* DeserializeFunction(char** str) {
//到达叶节点时,构建完毕,返回继续构建父节点
//双**表示取值
if (**str == '#') {
(*str)++;
return nullptr;
}
// 数字转换
int val = 0;
while (**str != '!' && **str != '\0') {
val = val * 10 + ((**str) - '0');
(*str)++;
}
TreeNode* root = new TreeNode(val);
// 序列到底了,构建完成
if (**str = '\0')return root;
else (*str)++;
//反序列化与序列化一致,都是前序
root->left = DeserializeFunction(str);
root->right = DeserializeFunction(str);
return root;
}
TreeNode* Deserialize(char* str) {
if (str == "#")return nullptr;
TreeNode* res = DeserializeFunction(&str);
return res;
}
};
3.14 重建二叉树,给定节点数为 n 的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。
C++/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* @param preOrder int整型vector
* @param vinOrder int整型vector
* @return TreeNode类
*/
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
int n = preOrder.size();
int m = vinOrder.size();
//每个遍历都不能为0
if (n == 0 || m == 0)
return NULL;
//构建根节点
TreeNode* root = new TreeNode(preOrder[0]);
for (int i = 0; i < vinOrder.size(); i++) {
//找到中序遍历中的前序第一个元素
if (preOrder[0] == vinOrder[i]) {
//左子树的前序遍历
vector<int> leftpre(preOrder.begin() + 1, preOrder.begin() + i + 1);
//左子树的中序遍历
vector<int> leftvin(vinOrder.begin(), vinOrder.begin() + i);
//构建左子树
root->left = reConstructBinaryTree(leftpre, leftvin);
//右子树的前序遍历
vector<int> rightpre(preOrder.begin() + i + 1, preOrder.end());
//右子树的中序遍历
vector<int> rightvin(vinOrder.begin() + i + 1, vinOrder.end());
//构建右子树
root->right = reConstructBinaryTree(rightpre, rightvin);
break;
}
}
return root;
}
};
3.15 请根据二叉树的前序遍历,中序遍历恢复二叉树,并打印出二叉树的右视图
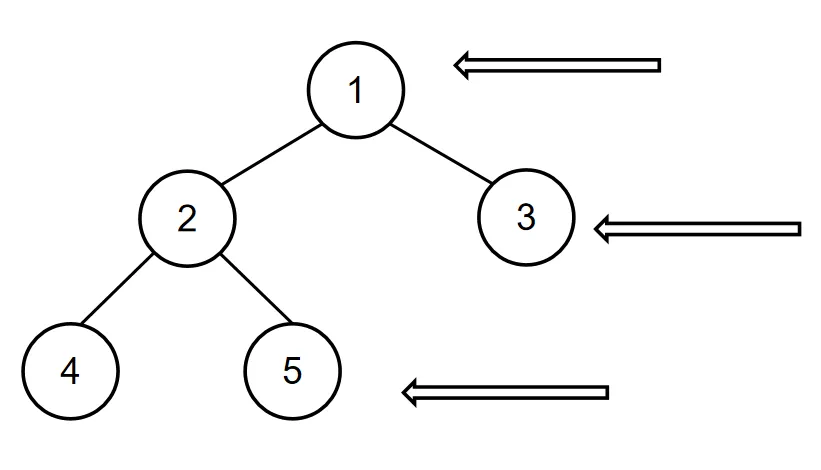
C++#include <stack>
#include <unordered_map>
#include <vector>
class Solution {
public:
/**
* 求二叉树的右视图
* @param preOrder int整型vector 先序遍历
* @param inOrder int整型vector 中序遍历
* @return int整型vector
*/
// 建树
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
int n = preOrder.size();
int m = vinOrder.size();
//每个遍历都不能为0
if (n == 0 || m == 0)
return NULL;
//构建根节点
TreeNode* root = new TreeNode(preOrder[0]);
for (int i = 0; i < vinOrder.size(); i++) {
//找到中序遍历中的前序第一个元素
if (preOrder[0] == vinOrder[i]) {
//左子树的前序遍历
vector<int> leftpre(preOrder.begin() + 1, preOrder.begin() + i + 1);
//左子树的中序遍历
vector<int> leftvin(vinOrder.begin(), vinOrder.begin() + i);
//构建左子树
root->left = reConstructBinaryTree(leftpre, leftvin);
//右子树的前序遍历
vector<int> rightpre(preOrder.begin() + i + 1, preOrder.end());
//右子树的中序遍历
vector<int> rightvin(vinOrder.begin() + i + 1, vinOrder.end());
//构建右子树
root->right = reConstructBinaryTree(rightpre, rightvin);
break;
}
}
return root;
}
// 右视图
vector<int> rightSideView(TreeNode* root){
unordered_map<int, int> map;//存放右边最深处的值
int max_depth = -1;//记录最大深度
stack<TreeNode*> nodes;//维护深度访问节点
stack<int> depths;//维护深度时的深度
nodes.push(root);
depths.push(0);
while(!nodes.empty()){
TreeNode* node = nodes.top();
nodes.pop();
int depth = depths.top();
depths.pop();
if(node != nullptr){
//维护二叉树的最大深度
max_depth = max(max_depth, depth);
//如果不存在对应深度的节点我们才插入,因为后面入栈的时候我后如的右节点的栈
if(map.find(depth) == map.end()){
map[depth] = node->val;
}
nodes.push(node->left);
nodes.push(node->right);
depths.push(depth + 1);
depths.push(depth + 1);
}
}
vector<int> res;
for(int i = 0; i < map.size(); i++){
res.push_back(map[i]);
}
return res;
}
vector<int> solve(vector<int>& preOrder, vector<int>& inOrder) {
// write code here
vector<int> res;
if(preOrder.size() == 0)return res;
// 建树
TreeNode* temp = reConstructBinaryTree(preOrder, inOrder);
return rightSideView(temp);
}
};
4.堆/栈/队列
4.1 使用两个栈模拟一个队列,思路:当插入时,直接插入 stack1,2、当弹出时,当 stack2 不为空,弹出 stack2 栈顶元素,如果 stack2 为空,将 stack1 中的全部数逐个出栈入栈 stack2,再弹出 stack2 栈顶元素
C++class Solution {
public:
void push(int node) {
stack1.push(node);
}
int pop() {
if (stack2.empty()) {
while (!stack1.empty()) {
int temp;
temp = stack1.top();
stack1.pop();
stack2.push(temp);
}
}
int temp2 = stack2.top();
stack2.pop();
return temp2;
}
private:
stack<int> stack1;
stack<int> stack2;
};
4.2 最小栈。定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的 min 函数,输入操作时保证 pop、top 和 min 函数操作时,栈中一定有元素。进阶:栈的各个操作的时间复杂度是O(1) ,空间复杂度是 O(n) 思路:用两个栈来做,另外一个栈保持栈顶元素是最小值。
C++#include <cstddef>
#include <stack>
#include <vector>
class Solution {
public:
void push(int value) {
node.push(value);
//空或者新元素较小,则入栈
if(node_min.empty() || node_min.top() > value)node_min.push(value);
//重复加入栈顶
else node_min.push(node_min.top());
}
void pop() {
node.pop();
node_min.pop();
}
int top() {
return node.top();
}
int min() {
return node_min.top();
}
private:
stack<int> node;
stack<int> node_min;
};
4.3 有效括号序列
C++#include <asm-generic/errno.h>
#include <vector>
class Solution {
public:
/**
* @param s string字符串
* @return bool布尔型
*/
bool isValid(string s) {
// write code here
stack<char> str;
for (int i = 0; i < s.length(); i++) {
if ((s[i] == '(') || (s[i] == '[') || (s[i] == '{') ) {
str.push(s[i]);
}
if ((s[i] == ')') || (s[i] == ']') || (s[i] == '}') ) {
if (s[i] == ')') {
if (!str.empty()) {
if (str.top() == '(') {
str.pop();
continue;
} else return false;
}
else return false;
}
if (s[i] == ']') {
if (!str.empty()) {
if (str.top() == '[') {
str.pop();
continue;
} else return false;
}
else return false;
}
if (s[i] == '}') {
if (!str.empty()) {
if (str.top() == '{') {
str.pop();
continue;
} else return false;
}
else return false;
}
}
}
if (str.empty())return true;
else return false;
}
};
4.4 滑动窗口的最大值,返回滑动窗口大小为size的窗口中的最大值。
C++#include <vector>
class Solution {
public:
/**
* @param num int整型vector
* @param size int整型
* @return int整型vector
*/
vector<int> maxInWindows(vector<int>& num, int size) {
// write code here
vector<int> max_num;
if(size == 0)return max_num;
int max;
for(int i = 0; i < num.size() - size + 1;i++){
max = num[i];
for(int j = i; j < size + i;j++){
if(max < num[j])max = num[j];
}
max_num.push_back(max);
}
return max_num;
}
};
4.5 输出数组最小K个数,思路:优先队列即PriorityQueue,是一种内置的机遇堆排序的容器,分为大顶堆与小顶堆。要找到最小的k个元素,只需要准备k个数字,之后每次遇到一个数字能够快速的与这k个数字中最大的值比较,每次将最大的值替换掉,那么最后剩余的就是k个最小的数字了。
C++class Solution {
public:
/**
* @param input int整型vector
* @param k int整型
* @return int整型vector
*/
vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
// write code here
vector<int> res;
if (k == 0 || input.size() == 0)
return res;
priority_queue<int> q;
//构建一个k个大小的堆
for (int i = 0; i < k; i++)
q.push(input[i]);
for (int i = k; i < input.size(); i++) {
//较小元素入堆
if (q.top() > input[i]) {
q.pop();
q.push(input[i]);
}
}
//堆中元素取出入vector
for (int i = 0; i < k; i++) {
res.push_back(q.top());
q.pop();
}
return res;
}
};
4.6 寻找数组中第K大个数,思路:快速排序(每次移动,可以找到一个标杆元素,然后将大于它的移到左边,小于它的移到右边,由此整个数组划分成为两部分,然后分别对左边和右边使用同样的方法进行排序,不断划分左右子段,直到整个数组有序。这也是分治的思想,将数组分化成为子段,分而治之。)
C++class Solution {
public:
/**
* @param a int整型vector
* @param n int整型
* @param K int整型
* @return int整型
*/
int part(vector<int>& r, int low, int hight) { //划分函数
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j) {
while (i < j &&r[j] <= pivot) { //从右向左开始找一个 大于 pivot的数值
j--;
}
if (i < j) {
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j &&r[i] > pivot) { //从左向右开始找一个 小于 pivot的数值
i++;
}
if (i < j) {
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
int Quicksort(vector<int>& r, int low, int hight, int K) {
int mid;
if (low < hight) {
mid = part(r, low, hight); // 返回基准元素位置
Quicksort(r, low, mid - 1, K); // 左区间递归快速排序
Quicksort(r, mid + 1, hight, K); // 右区间递归快速排序
}
return r[K-1];
}
int findKth(vector<int>& a, int n, int K) {
// write code here
return Quicksort(a, 0, n-1, K);
}
};
4.7 数据流中的中位数。思路:暴力方法,用vector来存取,调用sort函数排序。方法二,插入排序,每次来数据前对原数组进行插入排序。
C++#include <algorithm>
#include <vector>
class Solution {
public:
#define SCD static_cast<double>
vector<int> v;
void Insert(int num) {
if(v.empty())v.push_back(num);
else{
auto it = lower_bound(v.begin(), v.end(), num);
v.insert(it, num);
}
}
double GetMedian() {
int sz = v.size();
if(sz & 1)return SCD(v[sz >> 1]);
else{
return SCD((v[sz >> 1] + v[(sz-1) >> 1])) / 2;
}
}
};
4.8 表达式求值,写一个整数计算器,支持加减乘三种运算和括号。思路:遇到左括号,则将括号后的部分送入递归,处理子问题;
C++#include <cctype>
#include <string>
#include <vector>
class Solution {
public:
/**
* 返回表达式的值
* @param s string字符串 待计算的表达式
* @return int整型
*/
vector<int> function(string s, int index) {
int i;
stack<int> stack;
int num = 0;
char op = '+';
for (i = index; i < s.length(); i++) {
//数字转换成int数字
if (isdigit(s[i])) {
num = num * 10 + s[i] - '0';
if (i != s.length() - 1)continue;
}
//碰到'('时,把整个括号内的当成一个数字处理
if (s[i] == '(') {
//递归处理括号
vector<int> res = function(s, i + 1);
num = res[0];
i = res[1];
if (i != s.length() - 1)continue;
}
switch (op) {
//加减号先入栈
case '+':
stack.push(num);
break;
case '-':
//相反数
stack.push(-num);
break;
//优先计算乘号
case '*':
int temp = stack.top();
stack.pop();
stack.push(temp * num);
break;
}
num = 0;
//右括号结束递归
if (s[i] == ')')
break;
else
op = s[i];
}
int sum = 0;
//栈中元素相加
while (!stack.empty()) {
sum += stack.top();
stack.pop();
}
return vector<int> {sum, i};
}
int solve(string s) {
// write code here
return function(s, 0)[0];
}
};
5.哈希表
5.1 多数元素问题。数组中出现次数超过一半的数字,思路给定一个数组,找出数组中的众数,若有,返回众数,若没有,返回0。有三个方法:哈希表法(先遍历一遍数组,在map中存每个元素出现的次数,然后再遍历一次数组,找出众数)、排序法(使用sort(numbers.begin(),numbers.end())排序,超过一半的数肯定在数组中间)、候选法(最优解)加入数组中存在众数,那么众数一定大于数组的长度的一半。思想就是:如果两个数不相等,就消去这两个数,最坏情况下,每次消去一个众数和一个非众数,那么如果存在众数,最后留下的数肯定是众数。
C++//方法一、哈希表法 /*时间复杂度O(n),空间复杂度O(n)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
unordered_map<int,int> mp;
for(const int val : numbers) ++mp[val];
for(const int val : numbers){
if(mp[val] > (numbers.size() / 2))return val;
}
return 0;
}
};
C++//方法二、排序法,可以先将数组排序,然后可能的众数肯定在数组中间,然后判断一下。 /*时间复杂度O(nlogn),空间复杂度O(n)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
sort(numbers.begin(),numbers.end());
int cond = numbers[numbers.size() / 2];
int cnt;
for(const int k : numbers){
if(cond == k)++cnt;
}
if(cnt > numbers.size() / 2)return cond;
return 0;
}
};
C++//方法三、候选法,/*时间复杂度O(nlogn),空间复杂度O(1)*/
class Solution {
public:
/**
* @param numbers int整型vector
* @return int整型
*/
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
int cond = -1;
int cnt = 0;
for(int i = 0; i < numbers.size(); i++){
if(cnt == 0){
cond = numbers[i];
++cnt;
}
else{
if(cond == numbers[i])++cnt;
else --cnt;
}
}
cnt = 0;
for(const int k : numbers){
if(cond == k)++cnt;
}
if(cnt > numbers.size() / 2)return cond;
return 0;
}
};
//方法四、随机化,随机选一个数字计算次数,/时间复杂度O(n),空间复杂度O(1)/
C++class Solution {
public:
int majorityElement(vector<int>& nums) {
while (true) {
int candidate = nums[rand() % nums.size()];
int count = 0;
for (int num : nums)
if (num == candidate)
++count;
if (count > nums.size() / 2)
return candidate;
}
return -1;
}
};
5.2 返回数组中只出现一次的两个数字。一个整型数组里除了两个数字只出现一次,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
C++#include <any>
#include <unordered_map>
#include <vector>
class Solution {
public:
/**
* @param nums int整型vector
* @return int整型vector
*/
vector<int> FindNumsAppearOnce(vector<int>& nums) {
// write code here
unordered_map<int, int> mp;
vector<int> res;
for(const int val : nums){
mp[val]++;
}
for(int i = 0; i < nums.size(); i++){
if(mp[nums[i]] == 1){
res.push_back(nums[i]);
}
}
if(res[0] > res[1])swap(res[0], res[1]);
return res;
}
};
5.3 找到一个数组中缺失的第一个正整数
C++#include <unordered_map>
class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int minNumberDisappeared(vector<int>& nums) {
// write code here
unordered_map<int, int> mp;
int max = 1;
for(const int val : nums){
if(val > 0){
if(val > max)max = val;
mp[val]++;
}
}
for(int i = 1; i < max; i++){
if(mp[i] == 0)return i;
}
return max + 1;
}
};
6.递归/回溯
6.1 没有重复项数字的全排列,给出一组数字,返回该组数字的所有排列,例如:[1,2,3]的所有排列如下[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].思路:递归+回溯
C++#include <utility>
#include <vector>
class Solution {
public:
/**
* @param num int整型vector
* @return int整型vector<vector<>>
*/
void recursion(vector<vector<int>> &res, vector<int> &num, int index){
// 分支进入结尾,找到一种排列
if(index == num.size() - 1)res.push_back(num);
else{
// 遍历后续的元素
for(int i = index; i < num.size(); i++){
// 交换二者
swap(num[i], num[index]);
// 继续往后找
recursion(res, num, index + 1);
// 回溯
swap(num[i], num[index]);
}
}
}
vector<vector<int> > permute(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<vector<int>> res;
recursion(res, num, 0);
return res;
}
};
6.2 有重复项数字的全排列。思路:递归+回溯
C++class Solution {
public:
/**
* @param num int整型vector
* @return int整型vector<vector<>>
*/
void recursion(vector<vector<int>>& res, vector<int>& num, vector<int>& temp,
vector<int>& vis) {
// 分支进入结尾,找到一种排列
if (temp.size() == num.size()) {
res.push_back(temp);
return;
}
for (int i = 0; i < num.size(); i++) {
//如果该元素已经被加入了则不需要再加入了
if (vis[i])continue;
if (i > 0 && num[i - 1] == num[i] && !vis[i - 1])
//当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
continue;
//标记为使用过
vis[i] = 1;
//加入数组
temp.push_back(num[i]);
recursion(res, num, temp, vis);
//回溯
vis[i] = 0;
temp.pop_back();
}
}
vector<vector<int> > permuteUnique(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<int> vis(num.size(), 0);
vector<vector<int>> res;
vector<int> temp;
recursion(res, num, temp, vis);
return res;
}
};
6.3 岛屿的数量,给一个01矩阵,1代表是陆地,0代表海洋, 如果两个1相邻,那么这两个1属于同一个岛。我们只考虑上下左右为相邻。岛屿: 相邻陆地可以组成一个岛屿(相邻:上下左右) 判断岛屿个数。思路:矩阵中多处聚集着1,要想统计1聚集的堆数而不重复统计,那我们可以考虑每次找到一堆相邻的1,就将其全部改成0,而将所有相邻的1改成0的步骤又可以使用深度优先搜索(dfs):当我们遇到矩阵的某个元素为1时,首先将其置为了0,然后查看与它相邻的上下左右四个方向,如果这四个方向任意相邻元素为1,则进入该元素,进入该元素之后我们发现又回到了刚刚的子问题,又是把这一片相邻区域的1全部置为0,因此可以用递归实现。
C++#include <vector>
class Solution {
public:
/**
* 判断岛屿数量
* @param grid char字符型vector<vector<>>
* @return int整型
*/
void dfs(vector<vector<char>> &grid, int i, int j){
int n = grid.size();
int m = grid[0].size();
// 置为0
grid[i][j] = '0';
// 左右上下四个方向遍历
if(i - 1 >= 0 && grid[i - 1][j] == '1')dfs(grid, i - 1, j);
if(i + 1 < n && grid[i + 1][j] == '1')dfs(grid, i + 1, j);
if(j - 1 >= 0 && grid[i][j - 1] == '1')dfs(grid, i, j - 1);
if(j + 1 < m && grid[i][j + 1] == '1')dfs(grid, i, j + 1);
}
int solve(vector<vector<char> >& grid) {
// write code here
// 空矩阵的情况
int n = grid.size();
if(n == 0)return 0;
int m = grid[0].size();
// 记录岛屿数量
int count = 0;
// 遍历矩阵
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(grid[i][j] == '1'){
count++;
dfs(grid, i, j);
}
}
}
return count;
}
};
6.4 字符串的排列,输入一个长度为 n 字符串,打印出该字符串中字符的所有排列,你可以以任意顺序返回这个字符串数组。例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。(可能string中有重复的字符类似有重复数组的全排列)
C++#include <vector>
class Solution {
public:
/**
* @param str string字符串
* @return string字符串vector
*/
void recursion(vector<string>& res, string &num, string& temp,
vector<int>& vis) {
// 分支进入结尾,找到一种排列
if (temp.size() == num.size()) {
res.push_back(temp);
return;
}
for (int i = 0; i < num.size(); i++) {
//如果该元素已经被加入了则不需要再加入了
if (vis[i])continue;
if (i > 0 && num[i - 1] == num[i] && !vis[i - 1])
//当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
continue;
//标记为使用过
vis[i] = 1;
//加入数组
temp.push_back(num[i]);
recursion(res, num, temp, vis);
//回溯
vis[i] = 0;
temp.pop_back();
}
}
vector<string> Permutation(string str) {
// write code here
//先按字典序排序,使重复字符串相邻
sort(str.begin(), str.end());
//标记每个位置的字符是否被使用过s
vector<int> vis(str.size(), 0);
vector<string> res;
string temp;
recursion(res, str, temp, vis);
return res;
}
};
6.5 括号生成,给出n对括号,请编写一个函数来生成所有的由n对括号组成的合法组合。例如,给出n=3,解集为:"((()))", "(()())", "(())()", "()()()", "()(())"思路:递归+回溯。
C++#include <string>
#include <vector>
class Solution {
public:
/**
* @param n int整型
* @return string字符串vector
*/
void recursion(int left, int right, string temp, vector<string> &res, int n){
// 左右括号都用完了就加入结果
if(left == n && right == n){
res.push_back(temp);
return;
}
// 使用一次左括号
if(left < n){
recursion(left + 1, right, temp + '(', res, n);
}
// 使用右括号个数必须小于左括号
if(right < n && left > right){
recursion(left, right + 1, temp + ')', res, n);
}
}
vector<string> generateParenthesis(int n) {
// write code here
vector<string> res;
string temp;
recursion(0, 0, temp, res, n);
return res;
}
};
6.6 矩阵最长递增路径
C++#include <vector>
class Solution {
public:
/**
* 递增路径的最大长度
* @param matrix int整型vector<vector<>> 描述矩阵的每个数
* @return int整型
*/
//记录四个方向
int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int n, m;
int dfs(vector<vector<int>>& matrix, vector<vector<int>>& dp, int i, int j) {
if(dp[i][j] != 0)
return dp[i][j];
dp[i][j]++;
for(int k = 0; k < 4; k++){
int nexti = i + dirs[k][0];
int nextj = j + dirs[k][1];
//判断条件
if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] > matrix[i][j])
dp[i][j] = max(dp[i][j], dfs(matrix, dp, nexti, nextj) + 1);
}
return dp[i][j];
}
int solve(vector<vector<int> >& matrix) {
// write code here
int res = 0;
n = matrix.size();
m = matrix[0].size();
if (n == 0 || m == 0)return 0;
//i,j处的单元格拥有的最长递增路径
vector<vector<int>> dp (n, vector <int> (m));
// 遍历矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
res = max(res, dfs(matrix, dp, i, j));
}
}
return res;
}
};
7.动态规划
7.1 斐波那契数列,输入整数n,输出斐波那契数列的第n个值;可以当作动态规划问题;
C++class Solution {
public:
/**
* @param n int整型
* @return int整型
*/
int Fibonacci(int n) {
// write code here
int dp[50]{0};
dp[1] = 1, dp[2] = 1;
for(int i = 3; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
7.2 跳台阶,一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法(先后次序不同算不同的结果)。属于动态规划问题,分三步:1.定义问题;2.分解问题;3.子问题求解; 定义dp[i]是跳上第i个台阶的跳法,因为第i个台阶是i-1跳上去的或者是i-2跳上去的,所以dp[i]=dp[i-1]+dp[i-2],子问题dp[0] = 1, dp[1] =1;所以可以使用递归方法做了。
C++class Solution {
public:
/**
* @param number int整型
* @return int整型
*/
int jumpFloor(int number) {
// write code here
int dp[50]{0};
dp[0] = 1, dp[1] =1;
for (int i = 2; i <= number; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[number];
}
};
7.3 最小花费爬楼梯,给定一个整数数组cost,其中cost[i] 是从楼梯第i 个台阶向上爬需要支付的费用,下标从0开始。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
C++#include <vector>
class Solution {
public:
/**
* @param cost int整型vector
* @return int整型
*/
int minCostClimbingStairs(vector<int>& cost) {
// write code here
vector<int> dp(cost.size() + 1, 0);
dp[1] = 0, dp[2] = 0;
for(int i = 2; i <= cost.size(); i++){
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
7.4 两个字符串的最长公共子序列,思路,动态规划,1.定义dp[i][j]表示在s1中以i结尾,s2中以j结尾的字符串的最长公共子序列长度。2.根据“若是i位与j位的字符相等,则该问题可以变成1+dp[i−1][j−1],若i位与j位的字符不相等,取dp[i][j−1]或者dp[i−1][j]的较大值”补充矩阵dp[i][j]。3.dp的最后一个值就是最大子序列的长度,从最后一个值往前找,找到相等的值然后存起来,往左上角走相等的值对应的行或者列就是相等的字符,保存起来。
C++#include <stack>
#include <string>
#include <vector>
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* longest common subsequence
* @param s1 string字符串 the string
* @param s2 string字符串 the string
* @return string字符串
*/
string LCS(string s1, string s2) {
// write code here
if(s1 == "" || s2 == "")return "-1";
int len1 = s1.length();
int len2 = s2.length();
//dp[i][j]表示s1第i位,s2第j位为止的最长公共子序列长度
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
//遍历两个字符串每个位置求的最长长度
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(s1[i - 1] == s2[j - 1]){
dp[i][j] = 1 + dp[i - 1][j - 1];
}
else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 此时dp[len1][len2]为最大子序列的长度
//从动态规划数组末尾开始找最大子序列
stack<char> s;
int i = len1, j = len2;
while(dp[i][j]){
if(dp[i][j] == dp[i - 1][j])i--;
else if(dp[i][j] == dp[i][j - 1])j--;
else if(dp[i][j] > dp[i-1][j-1]){
i--;
j--;
s.push(s1[i]);
}
}
string res = "";
while(!s.empty()){
res += s.top();
s.pop();
}
return res != "" ? res : "-1"; ;
}
};
7.5 两个字符串的公共子串,思路:设1.dp[i][j]表示在str1中以第i个字符结尾在str2中以第j个字符结尾时的公共子串长度;2.遍历两个字符串填充dp数组,转移方程为:如果遍历到的该位两个字符相等,则此时长度等于两个前一位长度+1,dp[i][j]=dp[i−1][j−1]+1,如果遍历到该位时两个字符不相等,则置为0;每次更新dp[i][j]后,我们维护最大值,并更新该子串结束位置;3最后根据最大值结束位置使用substr即可截取出子串。
C++#include <iterator>
#include <stack>
#include <string>
#include <vector>
class Solution {
public:
/**
* longest common substring
* @param str1 string字符串 the string
* @param str2 string字符串 the string
* @return string字符串
*/
string LCS(string str1, string str2) {
// write code here
int len1 = str1.length();
int len2 = str2.length();
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
int max = 0;
int pos = 0;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1[i - 1] == str2[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = 0;
}
if (dp[i][j] > max){
max = dp[i][j]; // 将最大值放进去
pos = i;
}
}
}
return str1.substr(pos - max, max);
}
};
7.6 不同路径的数目,给定一个m∗n的矩阵,要求从矩阵的左上角走到右下角的不同路径数量(每次只能往下或者往右走). 方法一、递归:step 1:(终止条件) 当矩阵变长n减少到1的时候,很明显只能往下走,没有别的选择了,只有1条路径;同理m减少到1时也是如此。因此此时返回数量为1.step 2:(返回值) 对于每一级都将其两个子问题返回的结果相加返回给上一级。step 3:(本级任务) 每一级都有向下或者向右两种路径选择,分别进入相应分支的子问题。
C++class Solution {
public:
/**
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
// write code here
if(m == 1 || n == 1){
return 1;
}
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
}
};
方法二、动态规划:step 1:用dp[i][j]表示大小为i∗j的矩阵的路径数量,下标从1开始。step 2:(初始条件) 当i或者j为1的时候,代表矩阵只有一行或者一列,因此只有一种路径。step 3:(转移方程) 每个格子的路径数只会来自它左边的格子数和上边的格子数,因此状态转移为dp[i][j]=dp[i−1][j]+dp[i][j−1]。
C++#include <vector>
class Solution {
public:
/**
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
// write code here
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(i == 1){
dp[i][j] = 1;
continue;
}
if(j == 1){
dp[i][j] = 1;
continue;
}
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
};
7.7 给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。 思路:动态规划,1.设dp[i][j]为到矩阵a[i-1][j-1]的最小花费;2.分解:dp[i][j] = min(dp[i-1][j],dp[i][j-1])+a[i-1][j-1];注意第一行只能从左往右走,第一列只能从上往下走。3.矩阵dp右下角那个元素即为到达该地方的最小花费。
C++class Solution {
public:
/**
* @param matrix int整型vector<vector<>> the matrix
* @return int整型
*/
int minPathSum(vector<vector<int> >& matrix) {
// write code here
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (i == 1) {
dp[i][j] = dp[i][j - 1] + matrix[i - 1][j - 1];;
continue;
}
if (j == 1) {
dp[i][j] = dp[i - 1][j] + matrix[i - 1][j - 1];;
continue;
}
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i - 1][j - 1];
}
}
return dp[m][n];
}
};
7.8 把数字翻译成字符串,有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。现在给一串数字,返回有多少种可能的译码结果? 思路:动态规划,step 1:用辅助数组dp表示前i个数的译码方法有多少种。tep 2:对于一个数,我们可以直接译码它,也可以将其与前面的1或者2组合起来译码:如果直接译码,则dp[i]=dp[i−1];如果组合译码,则dp[i]=dp[i−2]。step 3:对于只有一种译码方式的,选上种dp[i−1]即可,对于满足两种译码方式(10,20不能)则是dp[i−1]+dp[i−2]。step 4:依次相加,最后的dp[length]即为所求答案。
C++class Solution {
public:
/**
* 解码
* @param nums string字符串 数字串
* @return int整型
*/
int solve(string nums) {
// write code here
//排除0
if (nums == "0")
return 0;
//排除只有一种可能的10 和 20
if (nums == "10" || nums == "20")
return 1;
//当0的前面不是1或2时,无法译码,0种
for (int i = 1; i < nums.length(); i++) {
if (nums[i] == '0')
if (nums[i - 1] != '1' && nums[i - 1] != '2')
return 0;
}
//辅助数组初始化为1
vector<int> dp(nums.length() + 1, 1);
for (int i = 2; i <= nums.length(); i++) {
//在11-19,21-26之间的情况
if ((nums[i - 2] == '1' && nums[i - 1] != '0') || (nums[i - 2] == '2' &&
nums[i - 1] > '0' && nums[i - 1] < '7'))
dp[i] = dp[i - 1] + dp[i - 2];
else
dp[i] = dp[i - 1];
}
return dp[nums.length()];
}
};
7.9 兑换零钱,给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。 思路:step 1:可以用dp[i]表示要凑出i元钱需要最小的货币数。step 2:一开始都设置为最大值aim+1,因此货币最小1元,即货币数不会超过aim.step 3:初始化dp[0]=0。step 4:后续遍历1元到aim元,枚举每种面值的货币都可能组成的情况,取每次的最小值即可,转移方程为dp[i]=min(dp[i],dp[i−arr[j]]+1).step 5:最后比较dp[aim]的值是否超过aim,如果超过说明无解,否则返回即可。
C++#include <vector>
class Solution {
public:
/**
* 最少货币数
* @param arr int整型vector the array
* @param aim int整型 the target
* @return int整型
*/
int minMoney(vector<int>& arr, int aim) {
// write code here
if(aim < 1)return 0;
vector<int> dp(aim + 1, aim + 1);
dp[0] = 0;
for(int i = 1; i <= aim; i++){
for(int j = 0; j < arr.size(); j++){
if(arr[j] <= i){
dp[i] = min(dp[i], dp[i - arr[j]] + 1);
}
}
}
return dp[aim] > aim ? -1 : dp[aim];
}
};
7.10 最长上升子序列,给定一个长度为 n 的数组 arr,求它的最长严格上升子序列的长度。所谓子序列,指一个数组删掉一些数(也可以不删)之后,形成的新数组。例如 [1,5,3,7,3] 数组,其子序列有:[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。 思路:动态规划,step 1:用dp[i]表示到元素i结尾时,最长的子序列的长度,初始化为1,因为只有数组有元素,至少有一个算是递增。step 2:第一层遍历数组每个位置,得到n个长度的子数组。step 3:第二层遍历相应子数组求对应到元素i结尾时的最长递增序列长度,期间维护最大值。step 4:对于每一个到i结尾的子数组,如果遍历过程中遇到元素j小于结尾元素,说明以该元素结尾的子序列加上子数组末尾元素也是严格递增的,因此转移方程为dp[i]=dp[j]+1。
C++class Solution {
public:
/**
* 给定数组的最长严格上升子序列的长度。
* @param arr int整型vector 给定的数组
* @return int整型
*/
int LIS(vector<int>& arr) {
// write code here
if(arr.empty())return 0;
//设置数组长度大小的动态规划辅助数组
vector<int> dp(arr.size(), 1);
int res = 1;
for (int i = 1; i < arr.size(); i++) {
for (int j = 0; j < i; j++) {
//可能j不是所需要的最大的,因此需要dp[i] < dp[j] + 1
if (arr[i] > arr[j] && dp[i] < dp[j] + 1) {
//i点比j点大,理论上dp要加1
dp[i] = dp[j] + 1;
//找到最大长度
res = max(res, dp[i]);
}
}
}
return res;
}
};
7.11 最长回文子串, 思路: 方法一:中心扩散,每个字符都可以尝试作为中心点看,会出现两种情况:可能是类似 aba 的字符串,也可能是类似 abba 的情况;只需要分别计算出以一个和两个字符作为中心点的子串,取出较大的长度即可;从left到right开始向两边扩散、比较,如果相等则继续扩散比较;如果不相等则剪枝,不用再继续扩散比较;计算每次比较的回文子串长度,取最大;时间复杂度 O(N^2),空间复杂度 O(1);
C++#include <algorithm>
#include <string>
class Solution {
public:
/**
* @param A string字符串
* @return int整型
*/
int helper(string A, int left, int right) {
while (left >= 0 && right < A.length()) {
if (A[left] == A[right]) {
left--;
right++;
continue;
}
break;
}
// "+1"是因为通过下标计算子串长度
// "-2"是因为上边的while循环是当索引为left和right不想等才退出循环的
// 因此此时的left和right是不满足的,需要舍弃
return right - left + 1 - 2;
}
int getLongestPalindrome(string A) {
// write code here
int n = A.length();
if (n < 2)return n;
int res = 0;
for (int i = 0; i < n; i++) {
int len = max(helper(A, i, i), helper(A, i, i + 1));
res = max(res, len);
}
return res;
}
};
方法二:动态规划,1.维护一个布尔型的二维数组dp,dp[i][j]表示 i 到 j 的子串是否是回文子串; 2.从长度0到字符串长度n进行判断; 3.选定起始下标 i 和终止下标 j, i 和 j 分别为要比较的字符串的左右边界指针; 4.从左右边界字符开始判断,即 A.charAt(i) == A.charAt(j); 5.当相等时,还要判断当前长度 c 是否大于1,不大于则表明只有两个字符的字符串,一个或两个字符肯定是回文串,如“11”; 6.判断的长度大于1时,因为最左右的字符已经相等,因此取决于上一次的子串是否是回文子串, 如 “12121”; 7.更新回文串的最大长度;
C++#include <algorithm>
#include <string>
#include <vector>
class Solution {
public:
/**
* @param A string字符串
* @return int整型
*/
int getLongestPalindrome(string A) {
// write code here
int n = A.length();
vector<vector<bool>> dp(n, vector<bool>(n, false));
int max = 0;
// 字符串长度差 c = j-i,即当前要比较的字符串长度
for(int c = 0; c <= n + 1; c++){
for(int i = 0; i < n -c; i++){
int j = c + i;
if(A[i] == A[j]){
// c <= 1表示只有两个字符的字符串,一个或两个字符肯定是回文串
if(c <= 1)dp[i][j] = true;
else{
// 对于两个字符以上的字符串
// 因为最左右的字符已经相等,因此取决于内层的子串是否是回文子串
dp[i][j] = dp[i + 1 ][j - 1];
}
// 更新回文串的最大长度,c代表判断的子串长度,越来越大
if(dp[i][j])max = c + 1;
}
}
}
return max;
}
};
7.12 数字字符串转换成合法的ip地址。 方法一:枚举法,tep 1:依次枚举这三个点的位置。step 2:然后截取出四段数字。step 3:比较截取出来的数字,不能大于255,且除了0以外不能有前导0,然后才能组装成IP地址加入答案中。
C++#include <string>
#include <vector>
class Solution {
public:
/**
* @param s string字符串
* @return string字符串vector
*/
vector<string> restoreIpAddresses(string s) {
// write code here
vector<string> res;
int n = s.length();
for (int i = 1; i < 4 && i < n - 2; i++) {
for (int j = i + 1; j < i + 4 && j < n - 1; j++) {
for (int k = j + 1; k < j + 4 && k < n; k++) {
if (n - k >= 4) {
continue;
}
string a = s.substr(0, i);
string b = s.substr(i, j - i);
string c = s.substr(j, k - j);
string d = s.substr(k);
//IP每个数字不大于255
if (stoi(a) > 255 || stoi(b) > 255 || stoi(c) > 255 || stoi(d) > 255)
continue;
//排除前导0的情况
if ((a.length() != 1 && a[0] == '0') || (b.length() != 1 && b[0] == '0') ||
(c.length() != 1 && c[0] == '0') || (d.length() != 1 && d[0] == '0'))
continue;
//组装IP地址
string temp = a + "." + b + "." + c + "." + d;
res.push_back(temp);
}
}
}
return res;
}
};
7.13 给定两个字符串 str1 和 str2 ,请你算出将 str1 转为 str2 的最少操作数。 你可以对字符串进行3种操作: 1.插入一个字符 2.删除一个字符 3.修改一个字符。 思路:step 1:初始条件: 假设第二个字符串为空,那很明显第一个字符串子串每增加一个字符,编辑距离就加1,这步操作是删除;同理,假设第一个字符串为空,那第二个字符串每增加一个字符,编剧距离就加1,这步操作是添加。 step 2:状态转移: 状态转移肯定是将dp矩阵填满,那就遍历第一个字符串的每个长度,对应第二个字符串的每个长度。如果遍历到str1[i]和 str2[j]的位置,这两个字符相同,这多出来的字符就不用操作,操作次数与两个子串的前一个相同,因此有dp[i][j]=dp[i−1][j−1];如果这两个字符不相同,那么这两个字符需要编辑,但是此时的最短的距离不一定是修改这最后一位,也有可能是删除某个字符或者增加某个字符,因此我们选取这三种情况的最小值增加一个编辑距离,即dp[i][j]=min(dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1]))+1。
C++class Solution {
public:
/**
* @param str1 string字符串
* @param str2 string字符串
* @return int整型
*/
int editDistance(string str1, string str2) {
// write code here
int n1 = str1.length();
int n2 = str2.length();
//dp[i][j]表示到str1[i]和str2[j]为止的子串需要的编辑距离
vector<vector<int> > dp(n1 + 1, vector<int>(n2 + 1, 0));
//初始化边界
for (int i = 1; i <= n1; i++)
dp[i][0] = dp[i - 1][0] + 1;
for (int i = 1; i <= n2; i++)
dp[0][i] = dp[0][i - 1] + 1;
//遍历第一个字符串的每个位置
for (int i = 1; i <= n1; i++)
//对应第二个字符串每个位置
for (int j = 1; j <= n2; j++) {
//若是字符相同,此处不用编辑
if (str1[i - 1] == str2[j - 1])
//直接等于二者前一个的距离
dp[i][j] = dp[i - 1][j - 1];
else
//选取最小的距离加上此处编辑距离1
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
return dp[n1][n2];
}
};
7.14 打家劫舍问题1,给定一个整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额(不能连着偷)。 思路,动态规划,step 1:用dp[i]表示长度为i的数组,最多能偷取到多少钱,只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。 step 2:(初始状态) 如果数组长度为1,只有一家人,肯定是把这家人偷了,收益最大,因此dp[1]=nums[0]。 step 3:(状态转移) 每次对于一个人家,我们选择偷他或者不偷他,如果我们选择偷那么前一家必定不能偷,因此累加的上上级的最多收益,同理如果选择不偷他,那我们最多可以累加上一级的收益。因此转移方程为 dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度,在nums中为下标。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int rob(vector<int>& nums) {
// write code here
//dp[i]表示长度为i的数组,最多能偷取多少钱
vector<int> dp(nums.size() + 1, 0);
//长度为1只能偷第一家
dp[1] = nums[0];
for (int i = 2; i <= nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
return dp[nums.size()];
}
};
7.15 打家劫舍问题2,数组头尾视为相邻,给定一个长度为n的整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。 思路:动态规划,step 1:使用原先的方案是:用dp[i]表示长度为i的数组,最多能偷取到多少钱,只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。 step 2:(初始状态) 如果数组长度为1,只有一家人,肯定是把这家人偷了,收益最大,因此dp[1]=nums[0]。 step 3:(状态转移) 每次对于一个人家,我们选择偷他或者不偷他,如果我们选择偷那么前一家必定不能偷,因此累加的上上级的最多收益,同理如果选择不偷他,那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度,在nums中为下标。 step 4:此时第一家与最后一家不能同时取到,那么我们可以分成两种情况讨论: 情况1:偷第一家的钱,不偷最后一家的钱。初始状态与状态转移不变,只是遍历的时候数组最后一位不去遍历。 情况2:偷最后一家的请,不偷第一家的钱。初始状态就设定了dp[1]=0,第一家就不要了,然后遍历的时候也会遍历到数组最后一位。 step 5:最后取两种情况的较大值即可。
C++class Solution {
public:
/**
* @param nums int整型vector
* @return int整型
*/
int rob(vector<int>& nums) {
// write code here
//dp[i]表示长度为i的数组,最多能偷取多少钱
vector<int> dp(nums.size() + 1, 0);
//选择偷了第一家
dp[1] = nums[0];
//最后一家不能偷
for (int i = 2; i < nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
int res = dp[nums.size() - 1];
//清除dp数组,第二次循环
dp.clear();
//不偷第一家
dp[1] = 0;
//可以偷最后一家
for (int i = 2; i <= nums.size(); i++)
//对于每家可以选择偷或者不偷
dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]);
//选择最大值
return max(res, dp[nums.size()]);
}
};
7.16 打家劫舍问题3,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root。除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。 思路:动态规划,我们可以用 f(o)表示选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;g(o)表示不选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;l和 r代表 o的左右孩子。当 o被选中时,o的左右孩子都不能被选中,故 o被选中情况下子树上被选中点的最大权值和为 l 和 r不被选中的最大权值和相加,即 f(o)=g(l)+g(r)。当 o不被选中时,o的左右孩子可以被选中,也可以不被选中。对于 o的某个具体的孩子 x,它对 o的贡献是 x被选中和不被选中情况下权值和的较大值。故 g(o)=max{f(l),g(l)}+max{f(r),g(r)}。至此,我们可以用哈希表来存 f和 g的函数值,用深度优先搜索的办法后序遍历这棵二叉树,我们就可以得到每一个节点的 f和 g。根节点的 f和 g的最大值就是我们要找的答案。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map <TreeNode*, int> f, g;
void dfs(TreeNode* node) {
if (!node) {
return;
}
dfs(node->left);
dfs(node->right);
f[node] = node->val + g[node->left] + g[node->right];
g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
}
int rob(TreeNode* root) {
dfs(root);
return max(f[root], g[root]);
}
};
8.字符串
8.1 字符串变形,对于一个长度为 n 字符串,我们需要对它做一些变形。首先这个字符串中包含着一些空格,就像"Hello World"一样,然后我们要做的是把这个字符串中由空格隔开的单词反序,同时反转每个字符的大小写。 比如"Hello World"变形后就变成了"wORLD hELLO"。 思路:step 1:遍历字符串,遇到小写字母,转换成大写,遇到大写字母,转换成小写,遇到空格正常不变。 step 2:第一次反转整个字符串,这样基本的单词逆序就有了,但是每个单词的字符也是逆的。 step 3:再次遍历字符串,以每个空间为界,将每个单词反转回正常。
C++class Solution {
public:
/**
* @param s string字符串
* @param n int整型
* @return string字符串
*/
string trans(string s, int n) {
// write code here
if (n == 0)
return s;
string res;
for (int i = 0; i < n; i++) {
//大小写转换
if (s[i] <= 'Z' && s[i] >= 'A')
res += s[i] - 'A' + 'a';
else if (s[i] >= 'a' && s[i] <= 'z')
res += s[i] - 'a' + 'A';
else
//空格直接复制
res += s[i];
}
//翻转整个字符串
reverse(res.begin(), res.end());
for (int i = 0; i < n; i++) {
int j = i;
//以空格为界,二次翻转
while (j < n && res[j] != ' ')
j++;
reverse(res.begin() + i, res.begin() + j);
i = j;
}
return res;
}
};
8.2 最长公共前缀,给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。 思路:step 1:处理数组为空的特殊情况。 step 2:因为最长公共前缀的长度不会超过任何一个字符串的长度,因此我们逐位就以第一个字符串为标杆,遍历第一个字符串的所有位置,取出字符。 step 3:遍历数组中后续字符串,依次比较其他字符串中相应位置是否为刚刚取出的字符,如果是,循环继续,继续查找,如果不是或者长度不足,说明从第i位开始不同,前面的都是公共前缀。 step 4:如果遍历结束都相同,最长公共前缀最多为第一个字符串。
C++class Solution {
public:
/**
* @param strs string字符串vector
* @return string字符串
*/
string longestCommonPrefix(vector<string>& strs) {
// write code here
int n = strs.size();
//空字符串数组
if (n == 0)
return "";
//遍历第一个字符串的长度
for (int i = 0; i < strs[0].length(); i++) {
char temp = strs[0][i];
//遍历后续的字符串
for (int j = 1; j < n; j++)
//比较每个字符串该位置是否和第一个相同
if (i == strs[j].length() || strs[j][i] != temp)
//不相同则结束
return strs[0].substr(0, i);
}
//后续字符串有整个字一个字符串的前缀
return strs[0];
}
};
8.3 验证IP地址是否有效 思路:step 1:写一个split函数(或者内置函数)。 step 2:遍历IP字符串,遇到.或者:将其分开储存在一个数组中。 step 3:遍历数组,对于IPv4,需要依次验证分组为4,分割不能缺省,没有前缀0或者其他字符,数字在0-255范围内。 step 4:对于IPv6,需要依次验证分组为8,分割不能缺省,每组不能超过4位,不能出现除数字小大写a-f以外的字符。
C++class Solution {
public:
/**
* 验证IP地址
* @param IP string字符串 一个IP地址字符串
* @return string字符串
*/
vector<string> split(string s, string spliter) {
vector<string> res;
int i;
//遍历字符串查找spliter
while ((i = s.find(spliter)) && i != s.npos) {
//将分割的部分加入vector中
res.push_back(s.substr(0, i));
s = s.substr(i + 1);
}
res.push_back(s);
return res;
}
int isIPv4(string IP) {
vector<string> s = split(IP, ".");
if (s.size() != 4)
return false;
for (int i = 0; i < s.size(); i++) {
//不可缺省,有一个分割为零,说明两个点相连
if (s[i].size() == 0)
return false;
//比较数字位数及不为零时不能有前缀零
if (s[i].size() < 0 || s[i].size() > 3 || (s[i][0] == '0' && s[i].size() != 1))
return false;
//遍历每个分割字符串,必须为数字
for (int j = 0; j < s[i].size(); j++)
if (!isdigit(s[i][j]))
return false;
//转化为数字比较,0-255之间
int num = stoi(s[i]);
if (num < 0 || num > 255)
return false;
}
return true;
}
int isIPv6(string IP) {
vector<string> s = split(IP, ":");
//IPv6必定为8组
if (s.size() != 8)
return false;
for (int i = 0; i < s.size(); i++) {
//每个分割不能缺省,不能超过4位
if (s[i].size() == 0 || s[i].size() > 4)
return false;
for (int j = 0; j < s[i].size(); j++) {
//不能出现a-fA-F以外的大小写字符
if (!(isdigit(s[i][j]) || (s[i][j] >= 'a' && s[i][j] <= 'f') ||
(s[i][j] >= 'A' && s[i][j] <= 'F')))
return false;
}
}
return true;
}
string solve(string IP) {
// write code here
if (IP.size() == 0)
return "Neither";
if (isIPv4(IP))
return "IPv4";
else if (isIPv6(IP))
return "IPv6";
return "Neither";
}
};
8.4 大数相加,以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。 数据范围:s.length,t.length≤100000,字符串仅由'0'~‘9’构成 思路:模拟加法运算
C++class Solution {
public:
/**
* 计算两个数之和
* @param s string字符串 表示第一个整数
* @param t string字符串 表示第二个整数
* @return string字符串
*/
string solve(string s, string t) {
// write code here
//若是其中一个为空,返回另一个
if (s.empty())
return t;
if (t.empty())
return s;
//让s为较长的,t为较短的
if (s.length() < t.length())
swap(s, t);
//进位标志
int carry = 0;
//从后往前遍历较长的字符串
for (int i = s.length() - 1; i >= 0; i--) {
//转数字加上进位
int temp = s[i] - '0' + carry;
//转较短的字符串相应的从后往前的下标
int j = i - s.length() + t.length();
//如果较短字符串还有
if (j >= 0)
//转数组相加
temp += t[j] - '0';
//取进位
carry = temp / 10;
//去十位
temp = temp % 10;
//修改结果
s[i] = temp + '0';
}
//最后的进位
if (carry == 1)
s = '1' + s;
return s;
}
};
9.双指针
9.1 判断字符串是否是回文结构(即前序遍历和后序遍历是一样的) 思路:使用双指针,一个指针在队首,一个指针在队尾,比较,首指针往后走,尾指针往前走,判断,一直到队尾指针下标大于队尾指针下标。
C++class Solution {
public:
/**
* @param str string字符串 待判断的字符串
* @return bool布尔型
*/
bool judge(string str) {
// write code here
//首指针
int left = 0;
//尾指针
int right = str.length() - 1;
while(left < right){
if(str[left] != str[right])return false;
left++;
right--;
}
return true;
}
};
9.2 合并区间,给出一组区间,请合并所有重叠的区间。请保证合并后的区间按区间起点升序排列。 输入:[[10,30],[20,60],[80,100],[150,180]] 返回值:[[10,60],[80,100],[150,180]]
C++/**
* struct Interval {
* int start;
* int end;
* Interval(int s, int e) : start(start), end(e) {}
* };
*/
class Solution {
public:
/**
* @param intervals Interval类vector
* @return Interval类vector
*/
static bool cmp(Interval &a, Interval &b) {
return a.start < b.start;
}
vector<Interval> merge(vector<Interval>& intervals) {
// write code here
vector<Interval> res;
if(intervals.size() == 0){
return res;
}
//按照区间首排序
sort(intervals.begin(), intervals.end(), cmp);
//放入第一个区间
res.push_back(intervals[0]);
//遍历后续区间,查看是否与末尾有重叠
for(int i = 1; i < intervals.size(); i++){
//区间有重叠,更新结尾
if(intervals[i].start <= res.back().end)
res.back().end = max(res.back().end, intervals[i].end);
//区间没有重叠,直接加入
else
res.push_back(intervals[i]);
}
return res;
}
};
9.3 反转字符串
C++#include <string>
class Solution {
public:
/**
* 反转字符串
* @param str string字符串
* @return string字符串
*/
string solve(string str) {
// write code here
string res;
int len = str.length();
for(int i = 0; i < len; i++){
res += str[len - 1 - i];
}
return res;
}
};
9.4 最长无重复子数组,给定一个长度为n的数组arr,返回arr的最长无重复元素子数组的长度,无重复指的是所有数字都不相同。子数组是连续的,比如[1,3,5,7,9]的子数组有[1,3],[3,5,7]等等,但是[1,3,7]不是子数组. 思路:step 1:构建一个哈希表,用于统计数组元素出现的次数。 step 2:窗口左右界都从数组首部开始,每次窗口优先右移右界,并统计进入窗口的元素的出现频率。 step 3:一旦右界元素出现频率大于1,就需要右移左界直到窗口内不再重复,将左边的元素移除窗口的时候同时需要将它在哈希表中的频率减1,保证哈希表中的频率都是窗口内的频率。 step 4:每轮循环,维护窗口长度最大值。
C++#include <map>
#include <unordered_map>
class Solution {
public:
/**
* @param arr int整型vector the array
* @return int整型
*/
int maxLength(vector<int>& arr) {
// write code here
// 哈希表内记录窗口内非重复的数字
unordered_map<int, int> mp;
int res = 0;
// 设置窗口左右界
for(int left = 0,right = 0; right < arr.size(); right++){
mp[arr[right]]++;
while(mp[arr[right]] > 1){
mp[arr[left++]]--;
}
res = max(res, right - left + 1);
}
return res;
}
};
9.5 盛水最多的容器,给定一个数组height,长度为n,每个数代表坐标轴中的一个点的高度,eight[i]是在第i点的高度,请问,从中选2个高度与x轴组成的容器最多能容纳多少水。
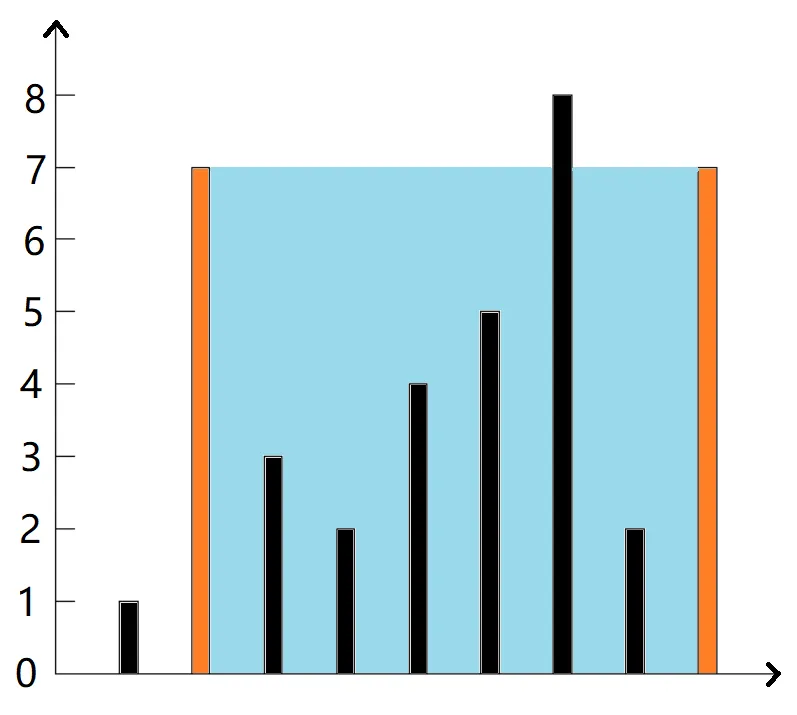 思路:可以利用贪心思想:我们都知道容积与最短边长和底边长有关,与长的底边一定以首尾为边,但是首尾不一定够高,中间可能会出现更高但是底边更短的情况,因此我们可以使用对撞双指针向中间靠,这样底边长会缩短,因此还想要有更大容积只能是增加最短变长,此时我们每次指针移动就移动较短的一边,因为贪心思想下较长的一边比较短的一边更可能出现更大容积。
step 1:优先排除不能形成容器的特殊情况。
step 2:初始化双指针指向数组首尾,每次利用上述公式计算当前的容积,维护一个最大容积作为返回值。
step 3:对撞双指针向中间靠,但是依据贪心思想,每次指向较短边的指针向中间靠,另一指针不变。
思路:可以利用贪心思想:我们都知道容积与最短边长和底边长有关,与长的底边一定以首尾为边,但是首尾不一定够高,中间可能会出现更高但是底边更短的情况,因此我们可以使用对撞双指针向中间靠,这样底边长会缩短,因此还想要有更大容积只能是增加最短变长,此时我们每次指针移动就移动较短的一边,因为贪心思想下较长的一边比较短的一边更可能出现更大容积。
step 1:优先排除不能形成容器的特殊情况。
step 2:初始化双指针指向数组首尾,每次利用上述公式计算当前的容积,维护一个最大容积作为返回值。
step 3:对撞双指针向中间靠,但是依据贪心思想,每次指向较短边的指针向中间靠,另一指针不变。
C++class Solution {
public:
/**
* @param height int整型vector
* @return int整型
*/
int maxArea(vector<int>& height) {
// write code here
//排除不能形成容器的情况
if (height.size() < 2)
return 0;
int res = 0;
//双指针左右界
int left = 0;
int right = height.size() - 1;
//共同遍历完所有的数组
while (left < right) {
//计算区域水容量
int capacity = min(height[left], height[right]) * (right - left);
//维护最大值
res = max(res, capacity);
//优先舍弃较短的边
if (height[left] < height[right])
left++;
else
right--;
}
return res;
}
};
9.6 接雨水问题
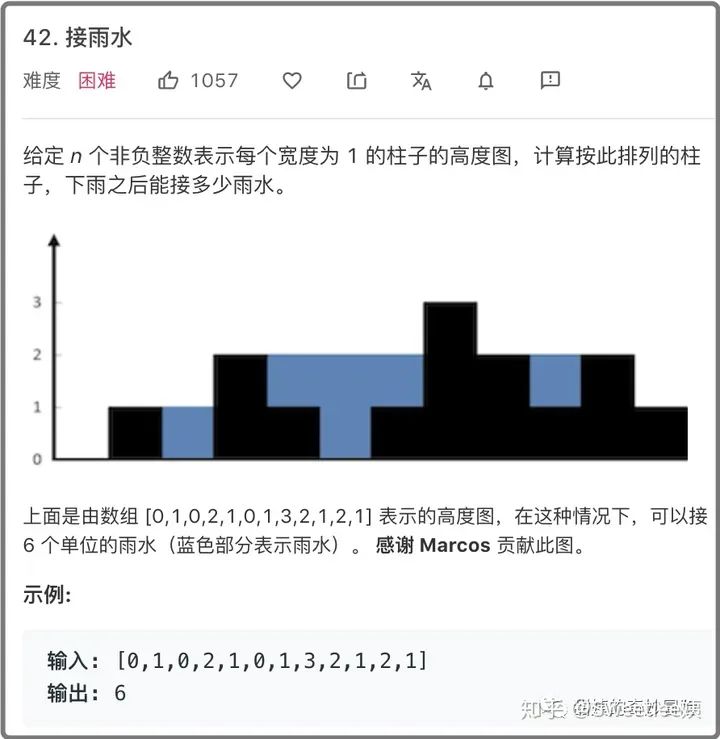
C++// 接雨水问题
#include<iostream>
using namespace std;
/*
*暴力法:每个柱子顶部可以储水的高度为:该柱子的左右两侧最大高度的较小者减去此柱子的高度。因此我们只需要遍历每个柱子,累加每个柱子可以储水的高度即可。
*/
int JieYuShui1(int height[], int len){
int res = 0;
// 遍历每个柱子
for (int i = 1; i < len - 1; i++) {
int leftMax = 0, rightMax = 0;
// 计算当前柱子左侧的柱子中的最大高度
for (int j = 0; j <= i; j++) {
leftMax = max(leftMax, height[j]);
}
// 计算当前柱子右侧的柱子中的最大高度
for (int j = i; j < len; j++) {
rightMax = max(rightMax, height[j]);
}
// 结果中累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
res += min(leftMax, rightMax) - height[i];
}
return res;
}
/*
*动态规划:对于每个柱子,我们都需要从两头重新遍历一遍求出左右两侧的最大高度,这里是有很多重复计算的,很明显最大高度是可以记忆化的,具体在这里可以用数组边递推边存储,也就是常说的动态规划,DP。
1定义二维dp数组 int[][] dp = new int[n][2],其中,dp[i][0] 表示下标i的柱子左边的最大值,dp[i][1] 表示下标i的柱子右边的最大值。2分别从两头遍历height数组,为 dp[i][0]和 dp[i][1] 赋值。3同方法1,遍历每个柱子,累加每个柱子可以储水的高度。
*/
int JieYuShui2(int height[], int len){
int res = 0;
if (len == 0) {
return 0;
}
// 定义二维dp数组
// dp[i][0] 表示下标i的柱子左边的最大值
// dp[i][1] 表示下标i的柱子右边的最大值
int dp[len][2];
dp[0][0] = height[0];
dp[len - 1][1] = height[len - 1];
for (int i = 1; i < len; i++) {
dp[i][0] = max(height[i], dp[i - 1][0]);
}
for (int i = len - 2; i >= 0; i--) {
dp[i][1] = max(height[i], dp[i + 1][1]);
}
// 遍历每个柱子,累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
for (int i = 1; i < len - 1; i++) {
res += min(dp[i][0], dp[i][1]) - height[i];
}
return res;
}
/*
*双指针:在上述的动态规划方法中,我们用二维数组来存储每个柱子左右两侧的最大高度,但我们递推累加每个柱子的储水高度时其实只用到了 dp[i][0]和 dp[i][1] 两个值,因此我们递推的时候只需要用 int leftMax 和 int rightMax 两个变量就行了。
*/
int JieYuShui3(int height[], int len){
int res = 0;
int leftMax = 0, rightMax = 0, left = 0, right = len - 1;
while (left <= right) {
if (leftMax <= rightMax) {
leftMax = max(leftMax, height[left]);
res += leftMax - height[left++];
} else {
rightMax = max(rightMax, height[right]);
res += rightMax - height[right--];
}
}
return res;
}
int main(){
int arr[] = {0,1,0,2,1,0,1,3,2,1,2,1};
int len = sizeof(arr) / sizeof(arr[0]);
int res = JieYuShui3(arr, len);
cout<<res<<endl;
return 0;
}
10.贪心算法
10.1 主持人调度,有 n 个活动即将举办,每个活动都有开始时间与活动的结束时间,第 i 个活动的开始时间是 starti ,第 i 个活动的结束时间是 endi ,举办某个活动就需要为该活动准备一个活动主持人。 step 1: 利用辅助数组获取单独各个活动开始的时间和结束时间,然后分别开始时间和结束时间进行排序,方便后面判断是否相交。 step 2: 遍历n个活动,如果某个活动开始的时间大于之前活动结束的时候,当前主持人就够了,活动结束时间往后一个。 step 3: 若是出现之前活动结束时间晚于当前活动开始时间的,则需要增加主持人。
C++class Solution {
public:
/**
* 计算成功举办活动需要多少名主持人
* @param n int整型 有n个活动
* @param startEnd int整型vector<vector<>> startEnd[i][0]用于表示第i个活动的开始时间,startEnd[i][1]表示第i个活动的结束时间
* @return int整型
*/
int minmumNumberOfHost(int n, vector<vector<int> >& startEnd) {
vector<int> start;
vector<int> end;
//分别得到活动起始时间
for (int i = 0; i < n; i++) {
start.push_back(startEnd[i][0]);
end.push_back(startEnd[i][1]);
}
//分别对开始和结束时间排序
sort(start.begin(), start.end());
sort(end.begin(), end.end());
int res = 0;
int j = 0;
for (int i = 0; i < n; i++) {
//新开始的节目大于上一轮结束的时间,主持人不变
if (start[i] >= end[j])
j++;
else
//主持人增加
res++;
}
return res;
}
};
11.模拟
11.1 旋转数组,一个数组A中存有 n 个整数,在不允许使用另外数组的前提下,将每个整数循环向右移 M。 输入:6,2,[1,2,3,4,5,6] 返回值:[5,6,1,2,3,4] 思路,先整体反转,再两个局部部分反转。
C++class Solution {
public:
/**
* 旋转数组
* @param n int整型 数组长度
* @param m int整型 右移距离
* @param a int整型vector 给定数组
* @return int整型vector
*/
vector<int> solve(int n, int m, vector<int>& a) {
// write code here
// 取余,因为m可能比n大
m = m % n;
// 第一次全部反转
reverse(a.begin(), a.end());
// 反转开头m个
reverse(a.begin(), a.begin() + m);
// 反转开头n个
reverse(a.begin() + m, a.end());
return a;
}
};
11.2 顺时针旋转矩阵,有一个NxN整数矩阵,请编写一个算法,将矩阵顺时针旋转90度。给定一个NxN的矩阵,和矩阵的阶数N,请返回旋转后的NxN矩阵。 输入[[1,2,3],[4,5,6],[7,8,9]],3 返回[[7,4,1],[8,5,2],[9,6,3]] 思路:先对角线反转(行转列,列转行),每一行反转
C++class Solution {
public:
/**
* @param mat int整型vector<vector<>>
* @param n int整型
* @return int整型vector<vector<>>
*/
vector<vector<int> > rotateMatrix(vector<vector<int> >& mat, int n) {
// write code here
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
swap(mat[i][j], mat[j][i]);
}
}
for(int i = 0; i < n; i++){
reverse(mat[i].begin(), mat[i].end());
}
return mat;
}
};
11.3 设计LRU缓存结构,设计LRU(最近最少使用)缓存结构,该结构在构造时确定大小,假设大小为 capacity ,操作次数是 n ,并有如下功能:
- Solution(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
- get(key):如果关键字 key 存在于缓存中,则返回key对应的value值,否则返回 -1 。
- set(key, value):将记录(key, value)插入该结构,如果关键字 key 已经存在,则变更其数据值 value,如果不存在,则向缓存中插入该组 key-value ,如果key-value的数量超过capacity,弹出最久未使用的key-value
思路:用一个双向链表,哈希表存key以及双向链表的迭代器。当需要插入新的数据项的时候,如果新数据项在链表中存在(一般称为命中),则把该节点移到链表头部,如果不存在,则新建一个节点,放到链表头部,若缓存满了,则把链表最后一个节点删除即可。在访问数据的时候,如果数据项在链表中存在,则把该节点移到链表头部,否则返回-1。这样一来在链表尾部的节点就是最近最久未访问的数据项。
C++#include <unordered_map>
class Solution {
list<pair<int, int>> dlist;//双向链表,pair是key-value的形式
unordered_map<int, list<pair<int, int>>::iterator> map;
int cap;
public:
Solution(int capacity) {
// write code here
cap = capacity;
}
int get(int key) {
// write code here
if (map.count(key)) {
//把这个放在头部,所以需要个tmp存着,然后删掉这个位置,再放到头部
auto tmp = *map[key];
dlist.erase(map[key]);
//map.erase(key);
dlist.push_front(tmp);//把它放在最前面
map[key] = dlist.begin();
//return tmp.second;
return dlist.front().second;
}
return -1;
}
void set(int key, int value) {
// write code here
if (map.count(key)) { //如果存在
dlist.erase(map[key]);//放在头部
//map.erase(key);
} else if (cap == dlist.size()) {
//先删掉末尾的
auto tmp = dlist.back();
map.erase(tmp.first);
dlist.pop_back();
}
dlist.push_front(pair<int, int>(key, value));
map[key] = dlist.begin(); //第一个迭代器
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* solution = new Solution(capacity);
* int output = solution->get(key);
* solution->set(key,value);
*/
11.4 设计LFU缓存结构,set(key, value):将记录(key, value)插入该结构 get(key):返回key对应的value值但是缓存结构中最多放K条记录,如果新的第K+1条记录要加入,就需要根据策略删掉一条记录,然后才能把新记录加入。这个策略为:在缓存结构的K条记录中,哪一个key从进入缓存结构的时刻开始,被调用set或者get的次数最少,就删掉这个key的记录;如果调用次数最少的key有多个,上次调用发生最早的key被删除这就是LFU缓存替换算法。实现这个结构,K作为参数给出 思路:但是我们还需要每次最快找到最久未使用的频率最小的节点,这时候我们可以考虑使用一个全局变量,跟踪记录最小的频率,有了最小的频率,怎样直接找到这个频率最小的节点,还是使用哈希表,key值记录各个频率,而value值就是后面接了一串相同频率的节点。如何保证每次都是最小频率的最久为使用,我们用双向链表将统一频率的节点连起来就好了,每次新加入这个频率的都在链表头,而需要去掉的都在链表尾。这样我们方法就是双哈希表。
C++class Solution {
public:
/**
* lfu design
* @param operators int整型vector<vector<>> ops
* @param k int整型 the k
* @return int整型vector
*/
//用list模拟双向链表,双向链表中数组第0位为频率,第1位为key,第2位为val
//频率到双向链表的哈希表
unordered_map<int, list<vector<int> > > freq_mp;
//key到双向链表节点的哈希表
unordered_map<int, list<vector<int> > ::iterator> mp;
//记录当前最小频次
int min_freq = 0;
//记录缓存剩余容量
int size = 0;
vector<int> LFU(vector<vector<int> >& operators, int k) {
// write code here
//记录输出
vector<int> res;
size = k;
//遍历所有操作
for (int i = 0; i < operators.size(); i++) {
auto op = operators[i];
if (op[0] == 1)
//set操作
set(op[1], op[2]);
else
//get操作
res.push_back(get(op[1]));
}
return res;
}
//调用函数时更新频率或者val值
void update(list<vector<int> >::iterator iter, int key, int value) {
//找到频率
int freq = (*iter)[0];
//原频率中删除该节点
freq_mp[freq].erase(iter);
//哈希表中该频率已无节点,直接删除
if (freq_mp[freq].empty()) {
freq_mp.erase(freq);
//若当前频率为最小,最小频率加1
if (min_freq == freq)
min_freq++;
}
//插入频率加一的双向链表表头,链表中对应:freq key value
freq_mp[freq + 1].push_front({freq + 1, key, value});
mp[key] = freq_mp[freq + 1].begin();
}
//set操作函数
void set(int key, int value) {
//在哈希表中找到key值
auto it = mp.find(key);
if (it != mp.end())
//若是哈希表中有,则更新值与频率
update(it->second, key, value);
else {
//哈希表中没有,即链表中没有
if (size == 0) {
//满容量取频率最低且最早的删掉
int oldkey = freq_mp[min_freq].back()[1];
//频率哈希表中删除
freq_mp[min_freq].pop_back();
if (freq_mp[min_freq].empty())
freq_mp.erase(min_freq);
//链表哈希表中删除
mp.erase(oldkey);
}
//若有空闲则直接加入,容量减1
else
size--;
//最小频率置为1
min_freq = 1;
//在频率为1的双向链表表头插入该键
freq_mp[1].push_front({1, key, value});
//哈希表key值指向链表中该位置
mp[key] = freq_mp[1].begin();
}
}
//get操作函数
int get(int key) {
int res = -1;
//查找哈希表
auto it = mp.find(key);
if (it != mp.end()) {
auto iter = it->second;
//根据哈希表直接获取值
res = (*iter)[2];
//更新频率
update(iter, key, res);
}
return res;
}
};
4.力扣top100
1.1每日温度,下一个更大元素。给一个数组,找到下一个比自身大的值在后面第几个。
输入:[73,74,75,71,69,72,76,73] 输出:[1,1,4,2,1,1,0,0] 思路一:暴力法,两层for循环。
C++class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int flag = 0;
vector<int> res;
int cnt = 0;
int len = temperatures.size();
for(int i = 0; i < len; i++){
for(int j = i + 1; j < len; j++){
if(temperatures[j] <= temperatures[i]){
cnt++;
}
if(temperatures[j] > temperatures[i]){
cnt++;
flag = 1;
break;
}
}
if(flag ==1 && cnt < len - i){
res.push_back(cnt);
}
else{
res.push_back(0);
}
cnt = 0;
flag = 0;
}
return res;
}
};
思路二:单调栈,空间换时间,定义一个栈存放数组元素的下标,遍历数组依次将数组元素的下标入栈,分三种情况考虑:
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
C++class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> st;
vector<int> result(temperatures.size(), 0);
st.push(0);
for (int i = 1; i < temperatures.size(); i++) {
// 情况一
if (temperatures[i] < temperatures[st.top()]) {
st.push(i);
}
// 情况二
else if (temperatures[i] == temperatures[st.top()]) {
st.push(i);
}
// 情况三
else {
while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
}
return result;
}
};
1.2 最大的正方形,在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
思路:动态规划,用dp(i,j)表示以(i,j)为右下角,且只包含1的正方形的边长最大值。 如果该位置的值是0,则 dp(i,j)=0,因为当前位置不可能在由1组成的正方形中; 如果该位置的值是 1,则 dp(i,j)的值由其上方、左方和左上方的三个相邻位置的 dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下: dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1 此外,还需要考虑边界条件。如果 i和 j中至少有一个为 0,则以位置 (i,j)为右下角的最大正方形的边长只能是1,因此 dp(i,j)=1。
C++class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};
1.3实现Trie(前缀树),前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
- Trie() 初始化前缀树对象。
- void insert(String word) 向前缀树中插入字符串 word 。
- boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
C++class Trie {
private:
bool isEnd;
Trie* next[26];
public:
Trie() {
isEnd = false;
memset(next, 0, sizeof(next));
}
void insert(string word) {
Trie* node = this;
for (char c : word) {
if (node->next[c-'a'] == NULL) {
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this;
for (char c : word) {
node = node->next[c - 'a'];
if (node == NULL) {
return false;
}
}
return node->isEnd;
}
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->next[c-'a'];
if (node == NULL) {
return false;
}
}
return true;
}
};
1.4课程优先学习问题,你这个学期必须选修 numCourses 门课程。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi],表示如果要学习课程 ai 则必须先学习课程 bi。请你判断是否可能完成所有课程的学习?
思路:本题是一道经典的「拓扑排序」问题。我们将每一门课看成一个节点;如果想要学习课程 AAA 之前必须完成课程 BBB,那么我们从 B到 A连接一条有向边。这样以来,在拓扑排序中,B一定出现在 A的前面。我们可以将深度优先搜索的流程与拓扑排序的求解联系起来,用一个栈来存储所有已经搜索完成的节点。我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候,我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。
C++class Solution {
private:
vector<vector<int>> edges;
vector<int> visited;
bool valid = true;
public:
void dfs(int u) {
visited[u] = 1;
for (int v: edges[u]) {
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
else if (visited[v] == 1) {
valid = false;
return;
}
}
visited[u] = 2;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
visited.resize(numCourses);
for (const auto& info: prerequisites) {
edges[info[1]].push_back(info[0]);
}
for (int i = 0; i < numCourses && valid; ++i) {
if (!visited[i]) {
dfs(i);
}
}
return valid;
}
};
1.5除自身以外数组的乘积,可以使用数组元素所有相乘再除以每个值得到,只需要考虑一下0的问题即可。如果要求不使用除法,则用下面的方法做。
思路:我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。
- 初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。
- 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。
- 同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
- 当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
C++class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
// L 和 R 分别表示左右两侧的乘积列表
vector<int> L(length, 0), R(length, 0);
vector<int> answer(length);
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
};
1.6最大乘积子数组,给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
思路:动态规划,如果我们用f(i) 来表示以第 i个元素结尾的乘积最大子数组的乘积,a表示输入参数 nums,那么很容易推导出这样的状态转移方程:f(i)=max{f(i−1)×ai,ai},但是这里需要考虑负数的问题,考虑当前位置如果是一个负数的话,那么我们希望以它前一个位置结尾的某个段的积也是个负数,这样就可以负负得正,并且我们希望这个积尽可能「负得更多」,可以得到这样的动态规划转移方程: fmax(i)=max{fmax(i−1)×ai,fmin(i−1)×ai,ai} fmin(i)=min{fmax(i−1)×ai,fmin(i−1)×ai,ai}
C++class Solution {
public:
int maxProduct(vector<int>& nums) {
vector <int> maxF(nums), minF(nums);
for (int i = 1; i < nums.size(); ++i) {
maxF[i] = max(maxF[i - 1] * nums[i], max(nums[i], minF[i - 1] * nums[i]));
minF[i] = min(minF[i - 1] * nums[i], min(nums[i], maxF[i - 1] * nums[i]));
}
return *max_element(maxF.begin(), maxF.end());
}
};
1.7单词拆分,给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
思路:动态规划,我们定义 dp[i]表示字符串 s前 i个字符组成的字符串 s[0..i−1]是否能被空格拆分成若干个字典中出现的单词。我们需要枚举 s[0..i−1]中的分割点 j ,看 s[0..j−1]组成的字符串 s1和 s[j..i−1]组成的字符串 s2拼接成的字符串也同样合法。出如下转移方程:dp[i]=dp[j] && check(s[j..i−1])对于检查一个字符串是否出现在给定的字符串列表里一般可以考虑哈希表来快速判断。
C++class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
auto wordDictSet = unordered_set <string> ();
for (auto word: wordDict) {
wordDictSet.insert(word);
}
auto dp = vector <bool> (s.size() + 1);
dp[0] = true;
for (int i = 1; i <= s.size(); ++i) {
for (int j = 0; j < i; ++j) {
if (dp[j] && wordDictSet.find(s.substr(j, i - j)) != wordDictSet.end()) {
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
};
1.8最长连续序列的长度
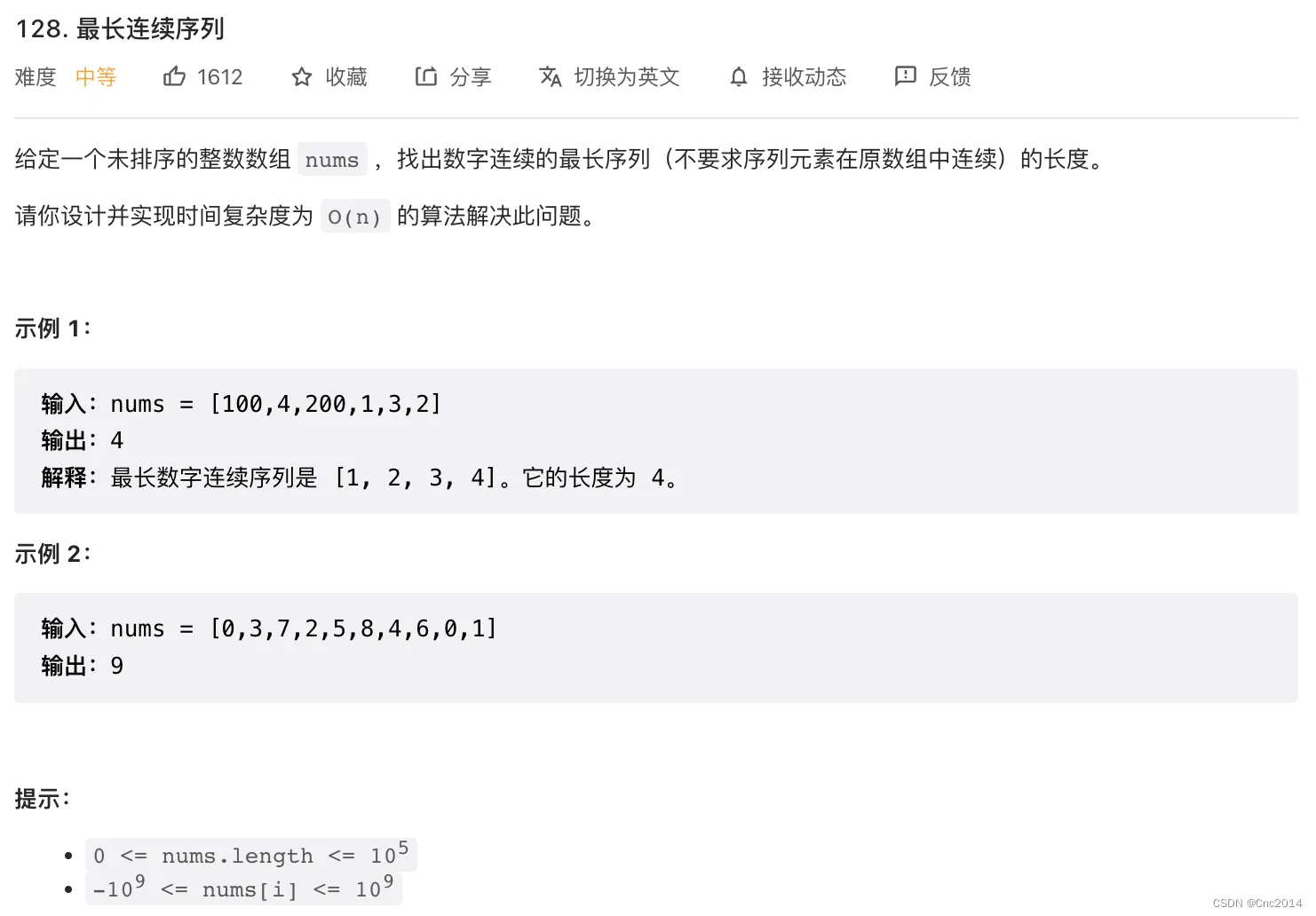 思路:哈希表,考虑枚举数组中的每个数 xxx,考虑以其为起点,不断尝试匹配 x+1,x+2,⋯是否存在,假设最长匹配到了 x+y,那么以 x为起点的最长连续序列即为 x,x+1,x+2,⋯ ,x+y其长度为 y+1,我们不断枚举并更新答案即可。仔细分析这个过程,我们会发现其中执行了很多不必要的枚举,如果已知有一个 x,x+1,x+2,⋯ ,x+y的连续序列,而我们却重新从 x+1,x+2或者是 x+y处开始尝试匹配,那么得到的结果肯定不会优于枚举 x为起点的答案,因此我们在外层循环的时候碰到这种情况跳过即可。
那么怎么判断是否跳过呢?由于我们要枚举的数 x一定是在数组中不存在前驱数 x−1的,不然按照上面的分析我们会从 x−1开始尝试匹配,因此我们每次在哈希表中检查是否存在 x−1即能判断是否需要跳过了。
思路:哈希表,考虑枚举数组中的每个数 xxx,考虑以其为起点,不断尝试匹配 x+1,x+2,⋯是否存在,假设最长匹配到了 x+y,那么以 x为起点的最长连续序列即为 x,x+1,x+2,⋯ ,x+y其长度为 y+1,我们不断枚举并更新答案即可。仔细分析这个过程,我们会发现其中执行了很多不必要的枚举,如果已知有一个 x,x+1,x+2,⋯ ,x+y的连续序列,而我们却重新从 x+1,x+2或者是 x+y处开始尝试匹配,那么得到的结果肯定不会优于枚举 x为起点的答案,因此我们在外层循环的时候碰到这种情况跳过即可。
那么怎么判断是否跳过呢?由于我们要枚举的数 x一定是在数组中不存在前驱数 x−1的,不然按照上面的分析我们会从 x−1开始尝试匹配,因此我们每次在哈希表中检查是否存在 x−1即能判断是否需要跳过了。
C++class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> num_set;
for (const int& num : nums) {
num_set.insert(num);
}
int longestStreak = 0;
for (const int& num : num_set) {
if (!num_set.count(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.count(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = max(longestStreak, currentStreak);
}
}
return longestStreak;
}
};
1.9二叉树的最大路径和,二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。路径和 是路径中各节点值的总和。
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6 思路:递归,实现一个简化的函数 maxGain(node),该函数计算二叉树中的一个节点的最大贡献值,具体而言,就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径,使得该路径上的节点值之和最大。根据函数 maxGain 得到每个节点的最大贡献值之后,如何得到二叉树的最大路径和?对于二叉树中的一个节点,该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值,如果子节点的最大贡献值为正,则计入该节点的最大路径和,否则不计入该节点的最大路径和。维护一个全局变量 maxSum 存储最大路径和,在递归过程中更新 maxSum 的值,最后得到的 maxSum 的值即为二叉树中的最大路径和。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int maxSum = INT_MIN;
public:
int maxGain(TreeNode* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时,才会选取对应子节点
int leftGain = max(maxGain(node->left), 0);
int rightGain = max(maxGain(node->right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node->val + leftGain + rightGain;
// 更新答案
maxSum = max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node->val + max(leftGain, rightGain);
}
int maxPathSum(TreeNode* root) {
maxGain(root);
return maxSum;
}
};
1.10目标和,给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
思路: 方法一、回溯,数组 nums的每个元素都可以添加符号 +或 -,因此每个元素有 2 种添加符号的方法,n个数共有 2^n种添加符号的方法,对应2^n种不同的表达式。当 n个元素都添加符号之后,即得到一种表达式,如果表达式的结果等于目标数 target,则该表达式即为符合要求的表达式。
C++class Solution {
public:
int count = 0;
int findTargetSumWays(vector<int>& nums, int target) {
backtrack(nums, target, 0, 0);
return count;
}
void backtrack(vector<int>& nums, int target, int index, int sum) {
if (index == nums.size()) {
if (sum == target) {
count++;
}
} else {
backtrack(nums, target, index + 1, sum + nums[index]);
backtrack(nums, target, index + 1, sum - nums[index]);
}
}
};
方法二、动态规划,记数组的元素和为 sum,添加 -号的元素之和为 neg,则其余添加 +的元素之和为 sum−neg,得到的表达式的结果为(sum−neg)−neg=sum−2⋅neg=target即neg=(sum−target)/2;若上式成立,问题转化成在数组 nums中选取若干元素,使得这些元素之和等于 neg,计算选取元素的方案数。我们可以使用动态规划的方法求解。

C++class Solution {
public:
int count = 0;
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int& num : nums) {
sum += num;
}
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int n = nums.size(), neg = diff / 2;
vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int num = nums[i - 1];
for (int j = 0; j <= neg; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= num) {
dp[i][j] += dp[i - 1][j - num];
}
}
}
return dp[n][neg];
}
};
1.11汉明距离,两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
方法一、使用内置函数,大多数编程语言都内置了计算二进制表达中 111 的数量的函数。在工程中,我们应该直接使用内置函数。
C++class Solution {
public:
int hammingDistance(int x, int y) {
return __builtin_popcount(x ^ y);
}
};
方法二、移位实现位计数,具体地,记 s=x⊕y,我们可以不断地检查 s的最低位,如果最低位为1,那么令计数器加一,然后我们令 s整体右移一位,这样 s的最低位将被舍去,原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0为止。这样计数器中就累计了 s的二进制表示中 1的数量。
C++class Solution {
public:
int hammingDistance(int x, int y) {
int s = x ^ y, ret = 0;
while (s) {
ret += s & 1;
s >>= 1;
}
return ret;
}
};
1.12找到数组中所有消失的数字,
 思路:我们可以用一个哈希表记录数组 nums中的数字,由于数字范围均在 [1,n]中,记录数字后我们再利用哈希表检查 [1,n]中的每一个数是否出现,从而找到缺失的数字。由于数字范围均在 [1,n]中,我们也可以用一个长度为 n的数组来代替哈希表。这一做法的空间复杂度是 O(n)的。我们的目标是优化空间复杂度到 O(1)。由于 nums的数字范围均在 [1,n]中,我们可以利用这一范围之外的数字,来表达「是否存在」的含义。具体来说,遍历 nums,每遇到一个数 x,就让 nums[x−1]增加 n。由于 nums中所有数均在 [1,n]中,增加以后,这些数必然大于 n。最后我们遍历 nums,若 nums[i]未大于 n,就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。
思路:我们可以用一个哈希表记录数组 nums中的数字,由于数字范围均在 [1,n]中,记录数字后我们再利用哈希表检查 [1,n]中的每一个数是否出现,从而找到缺失的数字。由于数字范围均在 [1,n]中,我们也可以用一个长度为 n的数组来代替哈希表。这一做法的空间复杂度是 O(n)的。我们的目标是优化空间复杂度到 O(1)。由于 nums的数字范围均在 [1,n]中,我们可以利用这一范围之外的数字,来表达「是否存在」的含义。具体来说,遍历 nums,每遇到一个数 x,就让 nums[x−1]增加 n。由于 nums中所有数均在 [1,n]中,增加以后,这些数必然大于 n。最后我们遍历 nums,若 nums[i]未大于 n,就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。
C++class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n = nums.size();
for (auto& num : nums) {
int x = (num - 1) % n;
nums[x] += n;
}
vector<int> ret;
for (int i = 0; i < n; i++) {
if (nums[i] <= n) {
ret.push_back(i + 1);
}
}
return ret;
}
};
1.13找到字符串中所有字母异位词,给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。 思路:滑动窗口法,根据题目要求,我们需要在字符串 s 寻找字符串 p 的异位词。因为字符串 p 的异位词的长度一定与字符串 p 的长度相同,所以我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口,并在滑动中维护窗口中每种字母的数量;当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时,则说明当前窗口为字符串 p 的异位词。
C++class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int sLen = s.size(), pLen = p.size();
if (sLen < pLen) {
return vector<int>();
}
vector<int> ans;
vector<int> sCount(26);
vector<int> pCount(26);
for (int i = 0; i < pLen; ++i) {
sCount[s[i] - 'a']++;
pCount[p[i] - 'a']++;
}
if (sCount == pCount) {
ans.push_back(0);
}
for (int i = 0; i < sLen - pLen; ++i) {
sCount[s[i] - 'a']--;
sCount[s[i + pLen] - 'a']++;
if (sCount == pCount) {
ans.push_back(i + 1);
}
}
return ans;
}
};
1.14 路径总和2,给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
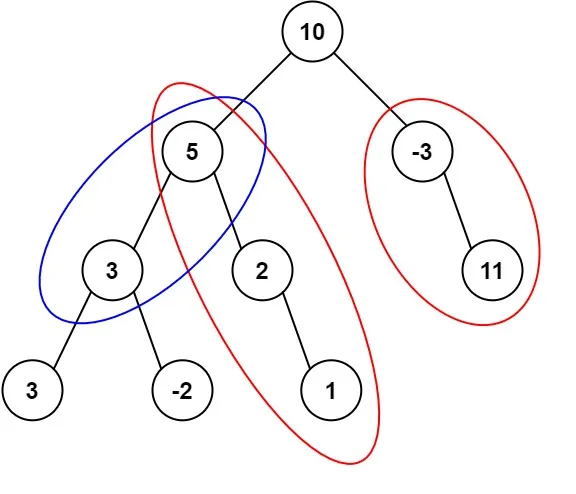
思路:深度优先搜索,我们首先想到的解法是穷举所有的可能,我们访问每一个节点 node,检测以 node为起始节点且向下延深的路径有多少种。我们递归遍历每一个节点的所有可能的路径,然后将这些路径数目加起来即为返回结果。
C++/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rootSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = 0;
if (root->val == targetSum) {
ret++;
}
ret += rootSum(root->left, targetSum - root->val);
ret += rootSum(root->right, targetSum - root->val);
return ret;
}
int pathSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root->left, targetSum);
ret += pathSum(root->right, targetSum);
return ret;
}
};
1.15分割等和子集,给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
思路:动态规划,给定一个只包含正整数的非空数组 nums[0],判断是否可以从数组中选出一些数字,使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0−1背包问题」。这道题与传统的「0−1背包问题」的区别在于,传统的「0−1背包问题」要求选取的物品的重量之和不能超过背包的总容量,这道题则要求选取的数字的和恰好等于整个数组的元素和的一半。类似于传统的「0−1 背包问题」,可以使用动态规划求解。 创建二维数组 dp,包含 nnn 行 target+1列,其中 dp[i][j]表示从数组的 [0,i][0,i][0,i] 下标范围内选取若干个正整数(可以是 0个),是否存在一种选取方案使得被选取的正整数的和等于j。初始时,dp中的全部元素都是 false。

C++class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return false;
}
int sum = accumulate(nums.begin(), nums.end(), 0);
int maxNum = *max_element(nums.begin(), nums.end());
if (sum & 1) {
return false;
}
int target = sum / 2;
if (maxNum > target) {
return false;
}
vector<vector<int>> dp(n, vector<int>(target + 1, 0));
for (int i = 0; i < n; i++) {
dp[i][0] = true;
}
dp[0][nums[0]] = true;
for (int i = 1; i < n; i++) {
int num = nums[i];
for (int j = 1; j <= target; j++) {
if (j >= num) {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n - 1][target];
}
};
1.16根据身高重建队列,假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
思路:从低到高考虑
C++class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](const vector<int>& u, const vector<int>& v) {
return u[0] < v[0] || (u[0] == v[0] && u[1] > v[1]);
});
int n = people.size();
vector<vector<int>> ans(n);
for (const vector<int>& person: people) {
int spaces = person[1] + 1;
for (int i = 0; i < n; ++i) {
if (ans[i].empty()) {
--spaces;
if (!spaces) {
ans[i] = person;
break;
}
}
}
}
return ans;
}
};
1.17除法求值,给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
思路:广度优先搜索,我们可以将整个问题建模成一张图:给定图中的一些点(变量),以及某些边的权值(两个变量的比值),试对任意两点(两个变量)求出其路径长(两个变量的比值)。 因此,我们首先需要遍历 equations数组,找出其中所有不同的字符串,并通过哈希表将每个不同的字符串映射成整数。 在构建完图之后,对于任何一个查询,就可以从起点出发,通过广度优先搜索的方式,不断更新起点与当前点之间的路径长度,直到搜索到终点为止。
C++class Solution {
public:
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
int nvars = 0;
unordered_map<string, int> variables;
int n = equations.size();
for (int i = 0; i < n; i++) {
if (variables.find(equations[i][0]) == variables.end()) {
variables[equations[i][0]] = nvars++;
}
if (variables.find(equations[i][1]) == variables.end()) {
variables[equations[i][1]] = nvars++;
}
}
// 对于每个点,存储其直接连接到的所有点及对应的权值
vector<vector<pair<int, double>>> edges(nvars);
for (int i = 0; i < n; i++) {
int va = variables[equations[i][0]], vb = variables[equations[i][1]];
edges[va].push_back(make_pair(vb, values[i]));
edges[vb].push_back(make_pair(va, 1.0 / values[i]));
}
vector<double> ret;
for (const auto& q: queries) {
double result = -1.0;
if (variables.find(q[0]) != variables.end() && variables.find(q[1]) != variables.end()) {
int ia = variables[q[0]], ib = variables[q[1]];
if (ia == ib) {
result = 1.0;
} else {
queue<int> points;
points.push(ia);
vector<double> ratios(nvars, -1.0);
ratios[ia] = 1.0;
while (!points.empty() && ratios[ib] < 0) {
int x = points.front();
points.pop();
for (const auto [y, val]: edges[x]) {
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;
points.push(y);
}
}
}
result = ratios[ib];
}
}
ret.push_back(result);
}
return ret;
}
};
1.18字符串解码,给定一个经过编码的字符串,返回它解码后的字符串。编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
输入:s = "3[a]2[bc]" 输出:"aaabcbc"
输入:s = "3[a2[c]]" 输出:"accaccacc"
思路:栈操作,本题中可能出现括号嵌套的情况,比如 2[a2[bc]],这种情况下我们可以先转化成 2[abcbc],在转化成 abcbcabcbc。我们可以把字母、数字和括号看成是独立的 TOKEN,并用栈来维护这些 TOKEN。具体的做法是,遍历这个栈: 如果当前的字符为数位,解析出一个数字(连续的多个数位)并进栈 如果当前的字符为字母或者左括号,直接进栈 如果当前的字符为右括号,开始出栈,一直到左括号出栈,出栈序列反转后拼接成一个字符串,此时取出栈顶的数字(此时栈顶一定是数字,想想为什么?),就是这个字符串应该出现的次数,我们根据这个次数和字符串构造出新的字符串并进栈 重复如上操作,最终将栈中的元素按照从栈底到栈顶的顺序拼接起来,就得到了答案。注意:这里可以用不定长数组来模拟栈操作,方便从栈底向栈顶遍历。
C++class Solution {
public:
string getDigits(string &s, size_t &ptr) {
string ret = "";
while (isdigit(s[ptr])) {
ret.push_back(s[ptr++]);
}
return ret;
}
string getString(vector <string> &v) {
string ret;
for (const auto &s: v) {
ret += s;
}
return ret;
}
string decodeString(string s) {
vector <string> stk;
size_t ptr = 0;
while (ptr < s.size()) {
char cur = s[ptr];
if (isdigit(cur)) {
// 获取一个数字并进栈
string digits = getDigits(s, ptr);
stk.push_back(digits);
} else if (isalpha(cur) || cur == '[') {
// 获取一个字母并进栈
stk.push_back(string(1, s[ptr++]));
} else {
++ptr;
vector <string> sub;
while (stk.back() != "[") {
sub.push_back(stk.back());
stk.pop_back();
}
reverse(sub.begin(), sub.end());
// 左括号出栈
stk.pop_back();
// 此时栈顶为当前 sub 对应的字符串应该出现的次数
int repTime = stoi(stk.back());
stk.pop_back();
string t, o = getString(sub);
// 构造字符串
while (repTime--) t += o;
// 将构造好的字符串入栈
stk.push_back(t);
}
}
return getString(stk);
}
};
1.19 前 K 个高频元素,给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
思路:粗暴排序法但是时间复杂度高,基于快速排序可以实现(内部找到)
C++class Solution {
public:
void qsort(vector<pair<int, int>>& v, int start, int end, vector<int>& ret, int k) {
int picked = rand() % (end - start + 1) + start;
swap(v[picked], v[start]);
int pivot = v[start].second;
int index = start;
for (int i = start + 1; i <= end; i++) {
// 使用双指针把不小于基准值的元素放到左边,
// 小于基准值的元素放到右边
if (v[i].second >= pivot) {
swap(v[index + 1], v[i]);
index++;
}
}
swap(v[start], v[index]);
if (k <= index - start) {
// 前 k 大的值在左侧的子数组里
qsort(v, start, index - 1, ret, k);
} else {
// 前 k 大的值等于左侧的子数组全部元素
// 加上右侧子数组中前 k - (index - start + 1) 大的值
for (int i = start; i <= index; i++) {
ret.push_back(v[i].first);
}
if (k > index - start + 1) {
qsort(v, index + 1, end, ret, k - (index - start + 1));
}
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
// 获取每个数字出现次数
unordered_map<int, int> occurrences;
for (auto& v: nums) {
occurrences[v]++;
}
vector<pair<int, int>> values;
for (auto& kv: occurrences) {
values.push_back(kv);
}
vector<int> ret;
qsort(values, 0, values.size() - 1, ret, k);
return ret;
}
};
1.20 买卖股票的最佳时机,给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0。
思路:一次遍历,一直记录最小值,然后当前值和最小值作差。
C++class Solution {
public:
int maxProfit(vector<int>& prices) {
int inf = 1e9;
int minprice = inf, maxprofit = 0;
for(int i = 0; i < prices.size(); i++){
maxprofit = max(maxprofit, prices[i] - minprice);
minprice = min(prices[i], minprice);
}
return maxprofit;
}
};
1.21,戳气球,有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。求所能获得硬币的最大数量。
思路:为了方便处理,我们对 nums数组稍作处理,将其两边各加上题目中假设存在的 nums[−1]和 nums[n],并保存在 val数组中,即 val[i]=nums[i−1]。之所以这样处理是为了处理 nums[−1],防止下标越界。我们观察戳气球的操作,发现这会导致两个气球从不相邻变成相邻,使得后续操作难以处理。于是我们倒过来看这些操作,将全过程看作是每次添加一个气球。我们定义方法 solve,令 solve(i,j)表示将开区间 (i,j)内的位置全部填满气球能够得到的最多硬币数。由于是开区间,因此区间两端的气球的编号就是 i和 j,对应着 val[i]和 val[j]。

C++class Solution {
public:
vector<vector<int>> rec;
vector<int> val;
int solve(int left, int right) {
if (left >= right - 1) {
return 0;
}
if (rec[left][right] != -1) {
return rec[left][right];
}
for (int i = left + 1; i < right; i++) {
int sum = val[left] * val[i] * val[right];
sum += solve(left, i) + solve(i, right);
rec[left][right] = max(rec[left][right], sum);
}
return rec[left][right];
}
int maxCoins(vector<int>& nums) {
int n = nums.size();
val.resize(n + 2);
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
val[0] = val[n + 1] = 1;
rec.resize(n + 2, vector<int>(n + 2, -1));
return solve(0, n + 1);
}
};
1.22买卖股票的最佳时机,含冷冻期,用户可以多次买卖股票,卖出股票后一天不能卖出(冷冻期)。
思路:动态规划,

class Solution { public: int maxProfit(vector<int>& prices) { if (prices.empty()) { return 0; } int n = prices.size(); // f[i][0]: 手上持有股票的最大收益 // f[i][1]: 手上不持有股票,并且处于冷冻期中的累计最大收益 // f[i][2]: 手上不持有股票,并且不在冷冻期中的累计最大收益 vector<vector<int>> f(n, vector<int>(3)); f[0][0] = -prices[0]; for (int i = 1; i < n; ++i) { f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]); f[i][1] = f[i - 1][0] + prices[i]; f[i][2] = max(f[i - 1][1], f[i - 1][2]); } return max(f[n - 1][1], f[n - 1][2]); } };
1.23删除无效括号,给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。返回所有可能的结果。答案可以按 任意顺序 返回。
思路:

C++class Solution {
public:
vector<string> res;
vector<string> removeInvalidParentheses(string s) {
int lremove = 0;
int rremove = 0;
for(char c : s){
if(c == '('){
lremove++;
}
else if(c == ')'){
if(lremove == 0)rremove++;
else lremove--;
}
}
helper(s, 0, lremove, rremove);
return res;
}
void helper(string str, int start, int lremove, int rremove){
if(lremove == 0 && rremove == 0){
if(isValid(str))res.push_back(str);
return;
}
for(int i = start; i < str.size(); i++){
if(i != start && str[i] == str[i - 1])continue;
// 如果剩余的字符无法满足去掉的数量要求,直接返回
if (lremove + rremove > str.size() - i) {
return;
}
// 尝试去掉一个左括号
if (lremove > 0 && str[i] == '(') {
helper(str.substr(0, i) + str.substr(i + 1), i, lremove - 1, rremove);
}
// 尝试去掉一个右括号
if (rremove > 0 && str[i] == ')') {
helper(str.substr(0, i) + str.substr(i + 1), i, lremove, rremove - 1);
}
}
}
inline bool isValid(const string & str){
int cnt = 0;
for(int i = 0; i < str.size(); i++){
if(str[i] == '(')cnt++;
else if(str[i] == ')'){
cnt--;
if(cnt < 0)return false;
}
}
return cnt == 0;
}
};
1.24 思路:
5.笔试经历
1.1 美团实习笔试第一题,小美入职美团后。特别喜欢meituan里的 mt这2个字符。他想写一份代码找到字符串里所有的'mf,"MT"。"mT"或者“Mt”。然后把他们都变成$$。请你写一份代码帮助也实现。
C++#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
getline(cin, s);
for (size_t i = 0; i < s.length() - 1; ++i) {
if (s[i] == 'm' || s[i] == 'M') {
if (s[i + 1] == 't' || s[i + 1] == 'T') {
s.replace(i, 2, "$$");
i++;
}
}
}
cout << s << endl;
return 0;
}
1.2 美团实习笔试第二题,小美拿到了一个n×n 的矩阵,其中每个元素是 0 或者 1。小美认为一个矩形区域是完美的,当且仅当该区域内 0 的数量恰好等于 1 的数量。现在,小美希望你回答有多少个i×i的完美矩形区域。
输入
4 1010 0101 1100 0011
输出
0 7 0 1
C++#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000;
int n;
char str[N][N];
int m[N][N], s[N][N];
int ans[N];
int GetPreSub(int x1, int y1, int x2, int y2) {
return s[x2 + 1][y2 + 1] - s[x1][y2 + 1] - s[x2 + 1][y1] + s[x1][y1];
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> str[i];
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
if (str[i][j] == '1') {
m[i + 1][j + 1] = 1;
} else {
m[i + 1][j + 1] = 0;
}
}
}
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + m[i][j];
}
}
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
for (int k = 0; k < n; k ++) {
if(i + k >= n || j + k >= n) {
break;
}
int sub = GetPreSub(i, j, i + k, j + k);
if (sub * 2 == (k + 1) * (k + 1)) {
ans[k] ++;
}
}
}
}
for (int i = 0; i < n; i ++) cout << ans[i] << endl;
return 0;
}
1.3 美团机器人招聘题1:第一行输入一个正整数n,代表菜品总数。第二行输入n个正整数ai,代表每道菜的价格。第三行输入两个正整数x和y,x代表满减的价格,y代表红包的价格。计算订单总价。
C++/*第一行输入一个正整数n,代表菜品总数。第二行输入n个正整数ai,代表每道菜的价格。
第三行输入两个正整数x和y,x代表满减的价格,y代表红包的价格。计算订单总价。
输入:
4
10 20 10 20
25 10
输出:
25
*/
#include <iostream>
using namespace std;
int main()
{
int n,a = 0,sum = 0;
int manjian,hongbao;
cin>>n;
for(int i = 0;i < n; i++){
cin>>a;
sum = sum + a;
}
cin>>manjian;
cin>>hongbao;
cout << sum - manjian - hongbao << endl;
return 0;
}
1.4 美团机器人招聘题2:定义以下三种单词是合法的:1.所有字母都是小写。例如: good。2.所有字母都是大写。例如。
3.第一个字母大写,后面所有字母都是小写。例如
。 现在小美拿到了一个单词,她每次操作可以修改任意一个字符的大小写。小美想知道最少操作几次可以使得单词变成合法的?C++/*小美定义以下三种单词是合法的:1.所有字母都是小写。例如: good。2.所有字母都是大写。例如:APP。
3.第一个字母大写,后面所有字母都是小写。例如:Alice。
现在小美拿到了一个单词,她每次操作可以修改任意一个字符的大小写。小美想知道最少操作几次可以使得单词变成合法的?
*/
#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
getline(cin, s);
int l = 0, h = 0;
for(int i = 0; i < s.size(); i++){
if(s[i] - 'a' >= 0)l++;
else h++;
}
int opt = min(l,h);
if((s[0] - 'a')<0)opt = min(opt,h - 1);
cout<<opt;
return 0;
}
1.5 美团机器人招聘题3:拿到了一个数组,她每次操作会将除了第x个元素的其余元素翻倍,一共操作了q次。请你帮小美计算操作结束后所有元素之和。
由于答案过大,请对1e9+7取模。
C++/*小美拿到了一个数组,她每次操作会将除了第x个元素的其余元素翻倍,一共操作了q次。请你帮小美计算操作结束后所有元素之和。
由于答案过大,请对1e9+7取模。
输入:
4 2
1 2 3 4
1 2
输出:
34
*/
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
int val,q,xi;
long sum=0;
const int MOD = 1e9 + 7;
cin >> n;
cin>>q;
vector<int> aa;
vector<int> bb;
for(int i = 0;i < n; i++){
cin>>val;
aa.push_back(val);
bb.push_back(val);
}
for(int i = 0; i < q; i++){
cin>>xi;
xi--;
for(int j = 0; j < n; j++){
if(j == xi)continue;
else{
bb[j] = bb[j] * 2 % MOD;
}
}
}
for(int i = 0; i < bb.size(); i++)sum+=bb[i];
std::cout<<sum % MOD;
return 0;
}
1.6 美团机器人招聘题4:求区间众数和
C++/*求区间众数和
第一行输入一个正整数n。第二行输入n个正整数,1<n<200000,1<=a<=2
输入
3
2 1 2
输出
9
*/
#include <cstdio>
#include <iostream>
#include <algorithm>
typedef long long LL;
const int N = 200010;
int n;
int a[N], tr[N * 2];
int sum[N];
int lowbit(int x) {
return x & -x;
}
void modify(int x, int k) {
for (int i = x; i <= 2 * n + 5; i += lowbit(i)) tr[i] += k;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
LL ans = 0;
modify(0 + n + 1, 1);
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1];
if (a[i] == 1) sum[i] += 1;
else sum[i] -= 1;
ans += query(sum[i] + n + 1) + (i - query(sum[i] + n + 1)) * 2;
modify(sum[i] + n + 1, 1);
}
printf("%lld", ans);
return 0;
}
1.7 美团机器人招聘题5:
C++#include<iostream>
#include<vector>
using namespace std;
const int N=200000;
void merge__(vector<int>& arr, vector<int>& tmp, int l, int mid, int r, int& ret) {
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (arr[i] > arr[j]) {
tmp[k++] = arr[j++];
ret += (mid - i + 1);
}
else {
tmp[k++] = arr[i++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= r) {
tmp[k++] = arr[j++];
}
for (k = 0, i = l; i <= r; ++i, ++k) {
arr[i] = tmp[k];
}
}
void merge_sort__(vector<int>& arr, vector<int>& tmp, int l, int r, int& ret) {
if (l >= r) {
return;
}
int mid = l + ((r - l) >> 1);
merge_sort__(arr, tmp, l, mid, ret);
merge_sort__(arr, tmp, mid + 1, r, ret);
merge__(arr, tmp, l, mid, r, ret);
}
int InversePairs(vector<int>& nums) {
// write code here
int ret = 0;
// 在最外层开辟数组
vector<int> tmp(nums.size());
merge_sort__(nums, tmp, 0, nums.size() - 1, ret);
return ret;
}
int main()
{
vector<int> q;
int n,a;
cin >> n;
int result;
for(int i=0;i<n;i++){
cin >>a;
q.push_back(a);
}
for(int i=0;i<n;i++){
q[i] = -q[i];
result = InversePairs(q);
cout << result<< ' ';
q[i] = -q[i];
}
return 0;
}
1.8美团删除数组问题小美有一个长度为 n 的数组 a1,a2,.·,an ,他可以对数组进行如下操作:
C++/*
问题描述:
小美有一个长度为 n 的数组 a1,a2,.·,an ,他可以对数组进行如下操作:
1.删除第一个元素 a1,同时数组的长度减一,花费为x
2.删除整个数组,花费为k*MEX(a),其中MEX(a)表示a中未出现过的最小非负整数。例如[0,1,2,4]的 MEX为3。
小美想知道将 a 数组全部清空的最小代价是多少。
输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T代表数据组数,每组测试数据描述如下第二行输入三个正整数:n,k,x
代表数组中的元素数量、删除整个数组的花费系数、删除单个元素的花费。第三行输入n个整数 a1, a2,...,an表示数组元素。
除此之外,保证所有的a之和不超过 2x105.
*/
/*
思路:动态规划+维护最小未出现的整数
dp[i]表示从i往后考虑的最小花费,最后的最小花费就是dp[0]和直接删除后续所有元素的最小值
对于删除后续所有的元素的选项,我们必须要知道mex是多少,可以在更新dp的过程中,用一个变量不断的更新当前的最小未出现的整数
虽然这里出现了两次循环的嵌套,但是并不会重置参数,因此复杂度是O(n)
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;
int main() {
int T;
cin >> T; // 读取测试数据组数
while (T--) {
long long n, k, x;
cin >> n >> k >> x;
vector<long long> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
// 动态规划数组dp[i]表示从i往后考虑的最小花费,最后最小花费就是dp[0]或者直接删除后续所有元素
vector<long long> dp(n + 1, LLONG_MAX);
dp[n] = 0;
int suffix_mex = 0;
set<int> vst;
for (int i = n-1; i >= 0; --i) {
vst.insert(a[i]);
while(vst.count(suffix_mex)){
suffix_mex++;
}
dp[i] = min(dp[i + 1] + x, k * suffix_mex);
}
// 输出最小花费
cout << dp[0] << endl;
}
return 0;
}
1.9大疆根据层序遍历字符串重建二叉树并找最大路径和
C++/*
问题描述:
题目描述:
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次。该路径 至少包含一个节点,目不一定经过根节点。路径和 是路径中各节点值的总和,以先序遍历给定一个二叉树的根节点root,返回其最大路径和。
输入描述:
输入:[1,2,3,4,5]
输出:11
*/
#include <bits/stdc++.h>
using namespace std;
#define emp -1
int maxSum = 0;
struct Node{
int value;
Node* left;
Node* right;
};
Node* createNode(){
Node* root = new Node();
root->left = nullptr;
root->right = nullptr;
return root;
}
void createFullBT_DFS(Node *&root, vector<int> &numbers, int len, int i) {
if(i <= len) {
root->value = numbers[i - 1];
if(2 * i <= len && numbers[2 * i - 1] != emp) {
root->left = createNode();
createFullBT_DFS(root->left, numbers, len, 2 * i);
}
if((2 * i + 1) <= len && numbers[2 * i] != emp) {
root->right = createNode();
createFullBT_DFS(root->right, numbers, len, 2 * i + 1);
}
}
}
int maxGain(Node* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时,才会选取对应子节点
int leftGain = max(maxGain(node->left), 0);
int rightGain = max(maxGain(node->right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node->value + leftGain + rightGain;
// 更新答案
maxSum = max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node->value + max(leftGain, rightGain);
}
void preOrder(Node *root) {
if(root != NULL) {
cout << root->value << " ";
preOrder(root->left);
preOrder(root->right);
}
}
int main(){
string str = "[1,2,3,4,5]";
string str_update = str.substr(1, str.length()-2);
char* str_input = (char*)str_update.c_str();
vector<int> nums;
int val = 0;
while(*str_input != '\0'){
if(*str_input != ','){
val = val * 10 + (*str_input - '0');
}
else{
nums.push_back(val);
val = 0;
}
str_input++;
}
nums.push_back(val);
Node* root = createNode();
createFullBT_DFS(root, nums, nums.size(), 1);
// preOrder(root);
maxGain(root);
cout << maxSum <<endl;
return 0;
}
1.10一个完整的软件项目往往会包含很多由代码和文档组成的源文件可能需要按照依赖关系来依次编译每个源文件。
C++/*
问题描述:
题目描述:
一个完整的软件项目往往会包含很多由代码和文档组成的源文件。编译器在编译整个项目的时候,可能需要按照依赖关系来依次编译每个源文件。比如,A.cpp 依赖 B.cpp,那么在编译的时候,编译器需要先编译 B.cpp,才能再编译 A.cpp。 假设现有 0,1,2,3 四个文件,0号文件依赖1号文件,1号文件依赖2号文件,3号文件依赖1号文件,则源文件的编译顺序为 2,1,0,3 或 2,1,3,0。现给出文件依赖关系,如 1,2,-1,1,表示0号文件依赖1号文件,1号文件依赖2号文件,2号文件没有依赖,3号文件依赖1号文件。请补充完整程序,返回正确的编译顺序。注意如有同时可以编译多个文件的情况,按数字升序返回一种情况即可,比如前述案例输出为:2,1,0,3
输入例子1:
"1,2,-1,1"
输出例子1:
"2,1,0,3"
*/
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
string compileSeq(string input) {
//首先完成有向无环图的构建
//统计图中各节点的个数 并标记头节点为-1
//使用优先队列 按照先小后大的顺序遍历输出节点值
int len = input.size();
/*********构建有向无环图(指向关系)*********/
map<int, vector<int>> mp;//first为先 second为后, 也就是second依赖于first
string tmp;
int idx = 0;
for(auto& s:input){
if(s != ',')
tmp += s;
else{
mp[stoi(tmp)].push_back(idx++);
string().swap(tmp);//清空string
}
}
if(!tmp.empty())
mp[stoi(tmp)].push_back(idx++);
/**********统计各节点个数 并保存头节点***********/
vector<int> indexcount(len, 0);//统计各节点个数
priority_queue<int, vector<int>, greater<>> pq;//保存节点
for(auto& m:mp){
if(m.first == -1){
for(auto& a:m.second){
pq.push(a);
indexcount[a] = -1;
}
}else{
for(auto& a:m.second)
++indexcount[a];
}
}
/************根据指向关系遍历图 并按照优先队列输出结果********/
vector<int> ans;
while(!pq.empty()){
int node = pq.top();
pq.pop();//输出了就需要从优先队列中弹出
ans.push_back(node);
for(auto& m:mp[node]){
if(--indexcount[m] == 0)//如果该节点是最后一次在图中出现 则放入队列中
pq.push(m);
}
}
/***********输出结果************/
string res;
for(auto& i:ans){
res += to_string(i);
res.push_back(',');
}
if(!res.empty())
res.pop_back();
return res;
}
};
int main(){
Solution OnecompileSeq;
string res = OnecompileSeq.compileSeq("1,2,-1,1");
cout << res << endl;
return 0;
}
1.11并查集模板
C++/*
问题描述:
并查集模板
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 100; // 节点数量
int f[N];
int init() {
// 初始化
for (int i=0; i<N; i++)
f[i] = i;
}
int getFather(int x) {
// 查询所在团伙代表人
return f[x]==x ? x : getFather(f[x]);
}
int merge(int a, int b) {
// 合并操作
f[getFather(a)] = getFather(b);
}
bool query(int a, int b) {
// 查询操作
return getFather(a) == getFather(b);
}
int main() {
init();
merge(3, 1); // 3和1是亲戚
merge(1, 4); // 1和4是亲戚
cout << getFather(3) << endl; // 输出3的团伙代表人+换行
cout << query(3, 1) << endl; // 输出3和1是否是亲戚+换行
}
1.12有向无环图节点的所有祖先
C++/*
问题描述:
有向无环图中一个节点的所有祖先。
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 ,1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ,1 和 3 。
- 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。
- 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
*/
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
vector<unordered_set<int>> anc(n); // 存储每个节点祖先的辅助数组
vector<vector<int>> e(n); // 邻接表
vector<int> indeg(n); // 入度表
// 预处理
for (const auto& edge: edges) {
e[edge[0]].push_back(edge[1]);
++indeg[edge[1]];
}
// 广度优先搜索求解拓扑排序
queue<int> q;
for (int i = 0; i < n; ++i) {
if (!indeg[i]) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v: e[u]) {
// 更新子节点的祖先哈希表
anc[v].insert(u);
for (int i: anc[u]) {
anc[v].insert(i);
}
--indeg[v];
if (!indeg[v]) {
q.push(v);
}
}
}
// 转化为答案数组
vector<vector<int>> res(n);
for (int i = 0; i < n; ++i) {
for (int j: anc[i]) {
res[i].push_back(j);
}
sort(res[i].begin(), res[i].end());
}
return res;
}
};
int main(){
Solution test;
int n = 8;
//[[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
vector<vector<int>> nums = {{0,3},{0,4},{1,3},{2,4},{2,7},{3,5},{3,6},{3,7},{4,6}};
vector<vector<int>> res = test.getAncestors(n, nums);
for(int i = 0; i < res.size(); i++){
for(int j = 0; j < res[i].size(); j++){
cout << res[i][j];
}
cout << endl;
}
return 0;
}
1.13滑动窗口找元素相加最接近某个值的,可以选择最多的元素数
c++/*
从数组中选择尽可能多的元素,只能连续选择,使得相加小于m,求最多可以选择几个数。输入为一个个数为n的数组和一个整数,输出为最多选择元素的个数。
*/
#include <iostream>
#include <vector>
using namespace std;
int maxConsecutiveElementsUnderSum(const std::vector<int>& nums, int m) {
int n = nums.size();
int max_count = 0; // 最多选择的元素个数
int current_sum = 0; // 当前窗口内元素的和
int left = 0; // 左指针
// 遍历数组,用右指针表示窗口的右端
for (int right = 0; right < n; ++right) {
current_sum += nums[right]; // 增加当前右指针对应的元素
// 当当前窗口和大于 m 时,收缩左边界
while (current_sum > m && left <= right) {
current_sum -= nums[left]; // 减去左指针的元素
left++; // 左指针右移
}
// 更新最多选择的元素个数
max_count = std::max(max_count, right - left + 1);
}
return max_count;
}
int main() {
vector<int> nums;
int n,m;
cin>>n>>m;
int val;
for(int i = 0; i < n; i++){
cin >> val;
nums.push_back(val);
}
int result = maxConsecutiveElementsUnderSum(nums, m);
cout << result << endl;
return 0;
}
1.14拼多多笔试1数组划分为k段,调整k段判断是否升序
c++/*
多多有一个长度为n的数组,依次采用如下策略对数组从小到大进行排序
1.将数组划分为k个非空子串(每个子串为原数组中连续数字组成的子序列)
2.调整k个子串的顺序,每个子串内元素顺序不变
3.将k个子串首尾相连,组成一个新的数组
以上策略不保证最终得到的数组有(单调递增)请你计算一下,对于给定的数组与划分数k,能否最终得到一个有序递增的序列
输入描述:
第一行一个数字T(T < 5),代表测试用例个数
对于每组测试用例:第一行两个数字:n,k,代表数组长度与划分子串个数,0<k<n<1e5
第二行n个数字a1,a2,…,an,0≤|ai|;≤ 1e14,保证数组内元素各不相同
输出描述:
对于每个测试用例,如果能够得到有序序列,输出“Tue"(不含引号),否则输出“False(不含引号)
示例:
输入:
3
5 3
8 12 7 -6 5
4 2
2 3 -6 4
5 5
10 6 8 -5 -10
输出:
True
False
True
思路 排序的同时也对原来的需要排序,然后判断块应该分割的次数,如果小于等于K则可以
*/
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
while(T--){
long long n, k;
cin >> n >> k;
vector<long long> arr(n);
for(auto &x : arr)cin >> x;
//Create a vector of pairs(value, original index)
vector<pair<long long, long long>> sorted_arr(n);
for(long long i = 0; i < n; i++){
sorted_arr[i] = {arr[i], i+1};//1-based indexing
}
// Sort the array based on values
sort(sorted_arr.begin(), sorted_arr.end());
// Count the number of blocks where indices are consecutive
long long m = 1;// At least one block
for(long long i = 1; i < n; i++){
if(sorted_arr[i].second != sorted_arr[i-1].second +1){
m++;
}
}
// If number of blocks <=k, it's possible
if(m <= k){
cout <<"True\n";
}
else{
cout<<"False\n";
}
}
}
1.15百度笔试时钟秒针转的圈数
c++/*
第一个的文字:小A的寝室里放着一个时钟。时钟有时针,分针,秒针三种指针。在某些时刻,时钟会记录下当前时间,格式为hh:mm:ss。
时钟上看不出日期,每天零点,三根指针都会归零。现在小A得到了一系列被记录的时间,且这些时间是按照先后顺序被记录的。
小A想让你算算,每两个时间点之间,秒针至少转了多少圈。注:一天有 24 个小时,1 小时有 60 分钟,1分钟有 60 秒,秒针一分钟转一圈。
输入描述:第一行一个整数 n(2 ≤n < 10e5),代表时间序列中时间点的个数。第二行n个字符串,每个字符串代表一个时间点,格式为hh:mm:ss(0 ≤ hh< 24, 0≤ mm< 60, 0 ≤ ss < 60).
输出描述:n -1个数,第i个数表示第i到i十1时间点秒针转过的圈数。输出结果和答案的绝对误差或相对误差不超过 10e-5 即被认为正确。
*/
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <iomanip>
using namespace std;
// Helper function to convert time in "hh:mm:ss" format to total seconds from midnight
int timeToSeconds(const string& time) {
int hh = stoi(time.substr(0, 2));
int mm = stoi(time.substr(3, 2));
int ss = stoi(time.substr(6, 2));
return hh * 3600 + mm * 60 + ss;
}
int main() {
int n;
cin >> n;
vector<string> times(n);
// Input all time points
for (int i = 0; i < n; ++i) {
cin >> times[i];
}
// Calculate and print the number of full rotations of the second hand between consecutive time points
for (int i = 1; i < n; ++i) {
int t1 = timeToSeconds(times[i - 1]);
int t2 = timeToSeconds(times[i]);
// If t2 is smaller, it means the time passed to the next day
if (t2 < t1) {
t2 += 24 * 3600; // add 24 hours in seconds
}
int secondsDiff = t2 - t1;
double rotations = secondsDiff / 60.0; // calculate the full rotations
printf("%.*f", 10, rotations);
// cout << setprecision(10) << rotations << endl; // print the result
}
return 0;
}
1.16百度笔试2正整数A包含B表示按位或运算
c++/*
我们称正整数A包含B,当且仅当(A|B)= A, |表示按位或运算,即B中的所有为1的二进制位,在A中都为1。现在给定n个正整数Ai,请你从中选出尽量少的整数,使得所有Ai,都至少被一个你选出来的整数包含。显然任何一个数总是包含其自身,即选择全部的数必定为一组合法答案(但不一定是最少的)。
输入描述:
第一行一个正整数n,接下来一行n个整数,第i个整数表示Ai。0≤ Ai< 262144, 1 ≤n≤2x1e5
输出描述:
一行一个整数,表示至少需要选出几个数字。
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
unordered_set<int> uniqueSet;
// Read input and add to the set to remove duplicates
for (int i = 0; i < n; ++i) {
cin >> a[i];
uniqueSet.insert(a[i]);
}
// Convert set back to vector
vector<int> uniqueNumbers(uniqueSet.begin(), uniqueSet.end());
// Sort in descending order to apply the greedy strategy
sort(uniqueNumbers.rbegin(), uniqueNumbers.rend());
int selectedCount = 0;
vector<bool> covered(uniqueNumbers.size(), false);
// For each number, see if it is necessary to cover the others
for (size_t i = 0; i < uniqueNumbers.size(); ++i) {
if (!covered[i]) {
selectedCount++;
for (size_t j = i + 1; j < uniqueNumbers.size(); ++j) {
if ((uniqueNumbers[i] | uniqueNumbers[j]) == uniqueNumbers[i]) {
covered[j] = true;
}
}
}
}
cout << selectedCount << endl;
return 0;
}
1.17得物笔试1字符串操作变成另外一个字符串
c++/*
c++实现以下问题:
小红一开始有 s串,s串是空串。她想获得一个字符串 t。
小红有四种操作:
1.在s串的开头添加一个字符,花费为p。
2.在s串的末尾添加一个字符,花费为p。
3.在s串的开头添加一个s串的子串,花费为 q。
4.在s串的末尾添加一个s串的子串,花费为 q。
每次操作都是基于当前的s串,有对应的花费。
小红想知道从s串变到t串的最小花费,你能帮帮她吗?
输入描述:
第一行输入一个字符串t,仅包含小写字符。
第二行输入两个正整数 p,q。
示例 1
输入
bbcabc
3 1
输出
11
说明:
s串先变成"c”,目前花费为3.
s串变成"bc",目前花费为6。
s串变成”bca”,目前花费为9.
s串变成"bcabc",目前花费为10.
s串变成“bbcabc",目前花费为11.
因此输出11。
*/
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main() {
// 读取输入
string t;
cin >> t;
int p, q;
cin >> p >> q;
int n = t.size();
vector<int> dp(n + 1, INT_MAX); // dp数组,初始为最大值
dp[0] = 0; // 空串到空串的花费为0
// 进行动态规划计算
for (int i = 1; i <= n; ++i) {
// 操作1和操作2: 添加一个字符
dp[i] = dp[i - 1] + p;
// 操作3和操作4: 添加一个子串
for (int j = 0; j < i; ++j) {
// 如果t的子串t[j:i]可以在s中形成,花费为q
string sub = t.substr(j, i - j);
if (t.substr(0, j).find(sub) != string::npos || t.substr(0, i - sub.size()).find(sub) != string::npos) {
dp[i] = min(dp[i], dp[j] + q);
}
}
}
// 输出最小花费
cout << dp[n] << endl;
return 0;
}
1.18 虹软笔试温控报警程序寄存器操作移位
c++/*
描述:编写一个温控报警程序,根据给定的三个32位寄存器的值reg1、reg2、reg3,以及报警调值 alarm 进行判
断,其中,reg1的第八位为状态位,状志位置1,表示传感器失效,reg2的0~3位为高位,reg3 的第 24~31位为
:位。温度寄存器的精度为0.1,范围为[-204, 204],需要计算温度的值,并判断温度是否大于报警调值,如果大于报
警闯值,则输出tue,否则输出false。状态位置1,直接输出ture
输入:reg1、reg2、reg3 的值(无符号32位整数,16进制表示),以及报警阈值alam(32 位有符号整数,10进
制表示)。输出:布尔值,表示温度是否大于报警值。
输入:88 18000A1F 12345678 120
解释:根据给定的奇存器值,可以提取温度的高位为0x,低位为0x12,计算得到温度值为181.8、由于温度值大于输出:tue报警阈值 120,因此输出 tue.
输入:88 12000a1a df12fe2d 120解释;根据给定的寄存器值,可以提取温度的高位为0xa,低位为0xd,计算得到温度值为74.3。由于温度值小于编出:false报警國值 120,因此输出false。
*/
#include <bits/stdc++.h>
using namespace std;
int main() {
unsigned int reg1,reg2,reg3;
cin >> hex >> reg1 >> hex >> reg2 >> hex >> reg3;
int alarm;
cin >> dec >> alarm;
if(reg1 & 0x100){
cout << "true" << endl;
cout << "111" << endl;
}
else{
reg2 &= 0x0f;
reg3 &= 0xff000000;
reg3 = reg3 >> 24;
reg2 = reg2 << 8;
unsigned int tmp = (reg2 + reg3);
unsigned int tmp2 = tmp - 0x7f8;
if(tmp2 > alarm*10)cout << "true" << endl;
else cout << "false" << endl;;
}
return 0;
}
1.19华为云笔试软件安装顺序
c++#
# wukun 华为云笔试
# 软件安装工具
# 有一个比较复杂的软件系统需要部署到客户提供的服务器上。该软件系统的安装过程非常繁琐,为了降低操作成本,需要开发一个工具实现自动化部署。软件的安装过程可以分成若干个小步骤,某些步骤间存在依赖关系,被依赖的步骤必须先执行完,才能执行后续的安装步骤。满足依赖条件的多个步骤可以并行执行。请你开发一个调度程序,以最短的时间完成软件的部署。
# 输入:
# 第一行:总步骤数 N(0<N<=10000)
# 第二行:N个以空格分隔的整数,代表每个步骤所需的时间。该行所有整数之和不大于int32
# 第三行开始的N行:表示每个步骤所依赖的其它步骤的编号(编号从1开始,行号减2表示步骤的编号),如果依赖多个步骤,用空格分隔。-1表示无依赖测试用例确保各个安装步骤不会出现循环依赖。
# 输出:
# 1个数字,代表最短执行时间。
# 样例1
# 输入:4
# 6 2 1 2
# -1
# 1
# 3
# 输出:9
# 样例2:
# 输入:4
# 1 2 3 4
# 2 3
# 3
# -1
# 1
# 输出:10
from collections import defaultdict, deque
def func(N, step_times, dependencies):
# 构建图和入度计数
graph = defaultdict(list)
in_degree = [0] * N
time_to_complete = [0] * N
# 填充依赖关系
for i in range(N):
for dep in dependencies[i]:
if dep != -1:
graph[dep - 1].append(i)
in_degree[i] += 1
# 使用队列处理入度为0的步骤
queue = deque()
for i in range(N):
if in_degree[i] == 0:
queue.append(i)
time_to_complete[i] = step_times[i]
# 进行拓扑排序
while queue:
current = queue.popleft()
current_completion_time = time_to_complete[current]
for neighbor in graph[current]:
in_degree[neighbor] -= 1
time_to_complete[neighbor] = max(time_to_complete[neighbor], current_completion_time + step_times[neighbor])
if in_degree[neighbor] == 0:
queue.append(neighbor)
return max(time_to_complete)
if __name__ == "__main__":
# 输入示例
N = int(input())
step_times = list(map(int, input().split()))
print(step_times)
dependencies = []
for _ in range(N):
deps = list(map(int, input().split()))
dependencies.append(deps)
# 输出最短执行时间
print(func(N, step_times, dependencies))
1.20经纬恒润笔试1-n整数十进制1出现的次数
c++/*
问题描述:
输入一个整数n,求1~n这n个整数的十进制表示中1出现的次数
例如,1~13中包含1的数字有1、10、11、12、13因此其出现6次
*/
#include <iostream>
using namespace std;
// 函数用于计算从1到n中'1'出现的次数
int countDigitOne(int n){
int count = 0;
long long factor = 1;// 用来表示当前分析的位(个位、十位、百位等)
while(n / factor > 0){
long long lower= n - (n / factor) * factor;// 当前位以下的数字
long long current=(n / factor) % 10;
long long higher=n / (factor * 10);
if(current == 0){
count += higher * factor;
}
else if(current == 1){
count += higher * factor + lower + 1;
}
else {
count +=(higher + 1) * factor;
}
factor *= 10;// 进入到下一位
}
return count;
}
int main(){
int n;
cin >> n;
cout<< countDigitOne(n)<<endl;
return 0;
}
1.21小米笔试最多可以装入多少件行李
c++/*
小米共有m个箱子用于打包行李,每个箱子承重为w。现有n件行李排成一行,重量为ai,
小米将从左向右开始打包。如果当前箱子装入该行李不会超重则优先装在当前箱子,
如果会超重则将当前箱子密封,将该行李装入下一个新的箱子中。小米更偏爱放在右边的行李,
所以为了能装入更多行李,他会选择从最左边开始连续地舍弃一些行李,以保证剩下的行李可以全部装完。
现在想知道,他最多可以装入多少件行李?
输入:
5 2 8
6 3 2 5 3
输出:
4
*/
#include <stdio.h>
int main(){
int n, m;
long long w;
scanf("%d %d %lld",&n,&m, &w);
long long weights[n];
for(int i=0;i<n; ++i)scanf("%lld",&weights[i]);
int boxcount =1;
long long currentweight =0;
int rightIndex=n-1;
while(rightIndex>=0){
if(currentweight + weights[rightIndex]<=w){
currentweight += weights[rightIndex];
} else {
boxcount++;
currentweight = weights[rightIndex];
}
rightIndex--;
if(boxcount>m){
rightIndex++;
break;
}
}
int itemsPacked=n - (rightIndex + 1);
printf("%d\n",itemsPacked);
return 0;
}
1.22滴滴笔试无向图依次删除节点求连通块的个数
c++/*
小A正在玩游戏,在游戏中一共有n个不同星球,星球间共有m条双向航道,小A的任务是摧毁这些星球。若有多个星球间两两可达,则我们称它们属于同一个联盟。特别的,若一个星球与其他星球间都没有航道,则也称其为一个联盟。小A将按照星球的编号从小到大依次摧毁各个星球,当一个星球被摧毁后,与之相连的航道也将相继被摧毁,现在小A想知道在每个星球被摧毁时还剩下多少个联盟。不同星球间可能有多条航道,但每条航道连接的两个星球必然不同。上述题意可以被简化为,给定n个点,m条边的无向图,按照编号大小依次删去各个节点,请问在每个节点被删去时,还剩下多少个连通块。保证给定图无自环,但可能有重边,
输入描述
第一行两个正整数n,m,表示星球数与航道数。接下来m行,每行2个正整数u,v,表示两星球间有一条航道。1<n,m<5e4
输出描述
输出一行n个正整数,表示答案。
样例输入
5 6
1 2
2 3
3 1
4 5
5 1
2 4
样例输出
1 2 1 1 0
*/
#include <stdio.h>
#define MAXNUM 1000
int Group[MAXNUM]; //记录图中节点是否被访问过
int dist[MAXNUM][MAXNUM]; //通过邻接矩阵保存图
void DFS(int i, int n);
int main()
{
int n, m, p, q, k = 0;
for (int i = 0; i < MAXNUM; i++)
{
for (int j = 0; j < MAXNUM; j++)
dist[i][j] = 0; //初始化邻接矩阵,初始值为0
Group[i] = 0; //同上
}
scanf("%d%d", &n, &m); //获取图的节点数n,和边数m
for (int i = 0; i < m; i++)
{
scanf("%d%d", &p, &q);
dist[p-1][q-1] = 1; //如果节点1和节3相连 则另dist[1][3]和dist[3][1]的值为1
dist[q-1][p-1] = 1;
}
for(int zz = 1; zz <= n; zz++){
for(int j = 1; j <= n; j++){ // 删除节点zz相连的边
p = zz;
q = j;
dist[p-1][q-1] = 0;
dist[q-1][p-1] = 0;
}
for (int i = 0; i < MAXNUM; i++) // 清零
{
Group[i] = 0;
}
for (int i = 0; i < n; i++)
{
if (Group[i] != 1)
{
DFS(i, n);
k++; //执行一次DFS就是k的值自增1,
}
}
printf("%d", k - zz); // k为删除边但没有删除节点的连通数 zz表示每次删除一个节点
k = 0;
}
return 0;
}
void DFS(int i,int n)
{
Group[i] = 1;
for (int j = 0; j < n; j++)
{
if (dist[i][j] == 1)
if (Group[j] != 1)
DFS(j, n);
}
}
1.23华为走迷宫防护服问题
c++/*
c++实现以下问题:
有一个 N x N 大小的迷宫。初始状态下,配送员位于迷宫的左上角,他希望前往迷宫的右下角。配送员只能沿若上下左右四个方向移动,从每个格子移动到相邻格子所需要的时间是 1个单位,他必须用最多 K 个(也可以少于 K 个)单位时间到达右下角格子。迷宫的每个格子都有辐射值,配送员必须穿着防护能力不低于相应辐射值的防护服,才能通过该格子。他希望知道,防护服的防护能力最少要达到多少,他才能顺利完成任务。注意:配送员需要通过迷宫的左上角和右下角,因此防护服的防护能力必须大于等于这两个格子的辐射值。
解答要求:
时间限制: C/C++1000ms,其他语言:2000ms内存限制: C/C++256MB,其他语言:512MB
输入:
前两行各包含一个正整数,分别对应 N 和 K后 N 行各包含 N 整数,以空格分隔,表示地图上每个位置的辐射值,2≤N≤100。 K≥2N-2,以保证题目有解。所有辐射值都是非负整数,绝对值不超过 1e4
输出:
一个整数,表示配送员穿着防护服的最低防护能力。
样例1
输入:
2
2
1 3
2 1
输出:2
解释:配送员可以选择通过左下角(辐射值为2)的路线,耗费2单位时间。
样例2
输入:
5
12
0 0 0 0 0
9 9 3 9 0
0 0 0 0 0
0 9 5 9 9
0 0 0 0 0
输出:3
解释:最优路线:往右2格,往下2格,往左2格,往下2格,往右4格,耗费12单位时间,经过格子的最大辐射值为3。
另外,在地图不变的情况下,如果K=16,输出为0;如果K=8,输出为5。
*/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = 1e9; // 定义一个足够大的值表示不可达
int N, K;
vector<vector<int>> radiation;
// 四个方向的移动
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
// 判断是否可以在指定的防护能力下从 (0,0) 到 (N-1,N-1)
bool canReach(int limit) {
if (radiation[0][0] > limit || radiation[N-1][N-1] > limit) {
return false;
}
vector<vector<bool>> visited(N, vector<bool>(N, false));
queue<pair<int, int>> q;
q.push({0, 0});
visited[0][0] = true;
int time = 0;
while (!q.empty()) {
int qsize = q.size();
if (time > K) return false; // 时间超过 K
while (qsize--) {
int x = q.front().first;
int y = q.front().second;
q.pop();
if (x == N-1 && y == N-1) {
return true; // 成功到达终点
}
for (int i = 0; i < 4; ++i) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < N && ny >= 0 && ny < N && !visited[nx][ny] && radiation[nx][ny] <= limit) {
visited[nx][ny] = true;
q.push({nx, ny});
}
}
}
++time; // 每次扩展一层,时间增加
}
return false; // 没有在 K 时间内到达终点
}
int main() {
// 读入 N 和 K
cin >> N >> K;
radiation.resize(N, vector<int>(N));
// 读入迷宫的辐射值
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
cin >> radiation[i][j];
}
}
// 二分查找防护能力
int low = 0, high = 1e4, ans = INF;
while (low <= high) {
int mid = (low + high) / 2;
if (canReach(mid)) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
// 输出结果
cout << ans << endl;
return 0;
}
本文作者:zzw
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 License 许可协议。转载请注明出处!